An elevator is accelerating upward at a rate of 6ftsec2 when a bolt from its celling falls to the floor of the lift (Distance=9.5feet). The time taken (in seconds) by the falling bolt to hit the floor is (take g=32ft/sec2)
The correct Answer is:(A)-p, (B)-v, (C)-s, (D)-q, (E)-u, (F)-t, (G)-r
To solve the problem of a bolt falling from the ceiling of an upward-accelerating elevator, we can follow these steps:
Step 1: Identify the effective acceleration
The elevator is accelerating upward at a rate of 6ft/s2 and the acceleration due to gravity g is 32ft/s2. Since the bolt is falling downwards while the elevator is accelerating upwards, we can find the effective acceleration acting on the bolt.
geffective=g−a=32ft/s2−6ft/s2=26ft/s2
Step 2: Use the equation of motion
We can use the second equation of motion to find the time taken for the bolt to hit the floor. The equation is:
s=ut+12geffectivet2
Where:
- s is the distance fallen (9.5 feet),
- u is the initial velocity (0 ft/s, since the bolt starts from rest),
- geffective is the effective acceleration (26 ft/s²),
- t is the time in seconds.
Substituting the known values into the equation:
9.5=0⋅t+12⋅26⋅t2
This simplifies to:
9.5=13t2
Step 3: Solve for t2
Now, we can rearrange the equation to solve for t2:
t2=9.513
Step 4: Calculate t
Now, we can calculate t:
t2=9.513≈0.730769
Taking the square root:
t=√0.730769≈0.854seconds
Final Answer
The time taken by the falling bolt to hit the floor is approximately 0.854 seconds.
---
The elevator is accelerating upward at a rate of 6ft/s2 and the acceleration due to gravity g is 32ft/s2. Since the bolt is falling downwards while the elevator is accelerating upwards, we can find the effective acceleration acting on the bolt.
We can use the second equation of motion to find the time taken for the bolt to hit the floor. The equation is:
- s is the distance fallen (9.5 feet),
- u is the initial velocity (0 ft/s, since the bolt starts from rest),
- geffective is the effective acceleration (26 ft/s²),
- t is the time in seconds.
Now, we can rearrange the equation to solve for t2:
Now, we can calculate t:
The time taken by the falling bolt to hit the floor is approximately 0.854 seconds.
Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - Assertion-Reason
20 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - Comprehension#1
3 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-02
37 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
A lift, initially at rest on the ground, starts ascending with constant acceleration 8m/s2 After 0.5 seconds, a bolt falls off the floor of the lift. The velocity of the lift at the instant the bolt hits the ground is m/s .[Take g=10m/s2]
View SolutionStarting from rest, A lift moves up with an acceleration of 2ms−2. In this lift , a ball is dropped from a height of 1.5m (with respect to floor of lift). The time taken by the ball to reach the floor of the lift is (g=10ms−2)
View SolutionAn elevator ascends an upward acceleration of 0.2 m/s2. At the instant it upwards speed in 3m/sec a loose bolt 5 m high form the floor drops from the ceiling of the elevator.Find the time until the bolt strikes the floor and the displacement it has fallen .
View SolutionAn elevator (lift) ascends with an upward acceleration of 1.2ms−2. At the instant when its upward speed is 2.4ms−1, a loose bolt drops from the ceiling of the elevator 2.7m above the floor of the elevator. Calculate (a) the time of flight of the bolt from the ceiling to the floor and (b) the distance it has fallen relaative to the elevator shaft.
View SolutionAn elevator is descending with uniform acceleration.To measure the acceleration, a person in the elevator drops a coin at momen the elevator strts. The coin is 6 ft asbove the floor of the elevator at the time it is dropped. The person observes that the coin strikes the floor in 1 second. Calculate these dta the acceleration of the elevator.
View SolutionA very broad elevator is going up vertically with a constant acceleration of 2m/s2. At the instant when its velocity is 4m/s a ball is projected form the floor of the lift with a speed of 4m/s relative to the floor at an elevation of 30∘. Time taken by the ball to return the floor is (g=10ms2)
View SolutionA very broad elevator is going up vertically with a constant acceleration of 2m/s2. At the instant when its velocity is 4m/s a ball is projected form the floor of the lift with a speed of 4m/s relative to the floor at an elevation of 30∘. Time taken by the ball to return the floor is (g=10ms2)
View SolutionA very broad elevator is going up vertically with a constant acceleration of 2m/s2. At the instant when its velocity is 4m/s a ball is projected form the floor of the lift with a speed of 4m/s relative to the floor at an elevation of 30∘. Time taken by the ball to return the floor is (g=10ms2)
View SolutionForce F is applied on upper pulley. If F = 30 t where t is time in second. Find the time when m1 loses contact with floor : (Take g=10m/s2)
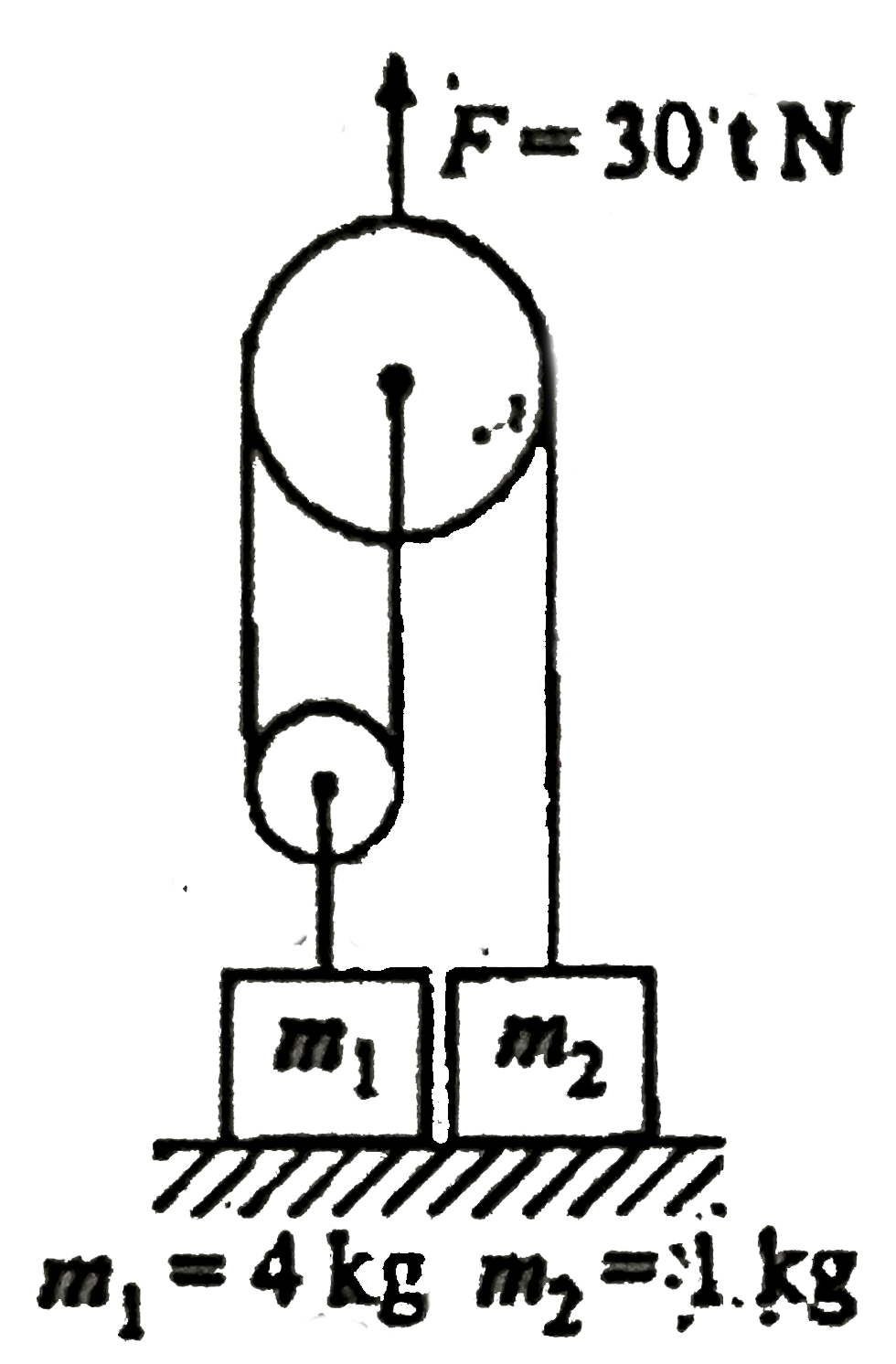
View SolutionAn elevator car whose floor to ceiling distance is equal to 2.7m starts ascending with constant acceleration 1.2m/s2. 2 s after the start, a bolt begins falling from the ceiling of the car. Find
(a)the time after which bolt hits the floor of the elevator.
(b)the net displacement and distance travelled by the bolt, with respect to earth. (Take g=9.8m/s2)
View Solution
