What is the ratio of P.E. w.r.t. ground and K.E. at the top most point of the projectile motion:-
The correct Answer is:C
To find the ratio of potential energy (P.E.) with respect to the ground and kinetic energy (K.E.) at the topmost point of projectile motion, we can follow these steps:
1. Understanding the Projectile Motion:
- In projectile motion, an object is launched at an angle θ with an initial velocity u.
- The motion can be analyzed in two components: horizontal (x-axis) and vertical (y-axis).
2. Identify the Kinetic Energy at the Topmost Point:
- At the topmost point of the projectile's trajectory, the vertical component of the velocity becomes zero, and only the horizontal component remains.
- The horizontal component of the velocity is given by:
vx=ucosθ
- Therefore, the kinetic energy (K.E.) at the topmost point is:
K.E.=12mv2=12m(ucosθ)2=12mu2cos2θ(Equation 1)
3. Calculate the Potential Energy at the Topmost Point:
- The height (h) at the topmost point can be calculated using the formula for maximum height in projectile motion:
h=u2sin2θ2g
- The potential energy (P.E.) with respect to the ground at this height is:
P.E.=mgh=mg(u2sin2θ2g)=12mu2sin2θ(Equation 2)
4. Finding the Ratio of P.E. to K.E.:
- Now, we need to find the ratio of potential energy to kinetic energy:
Ratio=P.E.K.E.=12mu2sin2θ12mu2cos2θ
- The 12mu2 terms cancel out:
Ratio=sin2θcos2θ=tan2θ
5. Final Result:
- Therefore, the ratio of potential energy with respect to the ground and kinetic energy at the topmost point of the projectile motion is:
tan2θ
- In projectile motion, an object is launched at an angle θ with an initial velocity u.
- The motion can be analyzed in two components: horizontal (x-axis) and vertical (y-axis).
- At the topmost point of the projectile's trajectory, the vertical component of the velocity becomes zero, and only the horizontal component remains.
- The horizontal component of the velocity is given by:
vx=ucosθ
- Therefore, the kinetic energy (K.E.) at the topmost point is:
K.E.=12mv2=12m(ucosθ)2=12mu2cos2θ(Equation 1)
- The height (h) at the topmost point can be calculated using the formula for maximum height in projectile motion:
h=u2sin2θ2g
- The potential energy (P.E.) with respect to the ground at this height is:
P.E.=mgh=mg(u2sin2θ2g)=12mu2sin2θ(Equation 2)
- Now, we need to find the ratio of potential energy to kinetic energy:
Ratio=P.E.K.E.=12mu2sin2θ12mu2cos2θ
- The 12mu2 terms cancel out:
Ratio=sin2θcos2θ=tan2θ
- Therefore, the ratio of potential energy with respect to the ground and kinetic energy at the topmost point of the projectile motion is:
tan2θ
Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-3
40 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-1
99 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
In a S.H.M. with amplitude 'A', what is the ratio of K.E. and P.E. at A2 distance from the mean position ?
View SolutionSelect the odd one w.r.t. ground tissue system is
View SolutionA particle collides with a smooth, surface with speed u at an angle θ. Coefficient of restitution is e. Find the ratio of the horizontal ranges of two consecutive projectile motions
View SolutionIf T is the total time of flight, h is the maximum height and R is the range for horizontal motion, the x and y coordinates of projectile motion and time t are related as
View SolutionIn a typical projectile motion, tangential acceleration at the topmost point P of the trajectory is
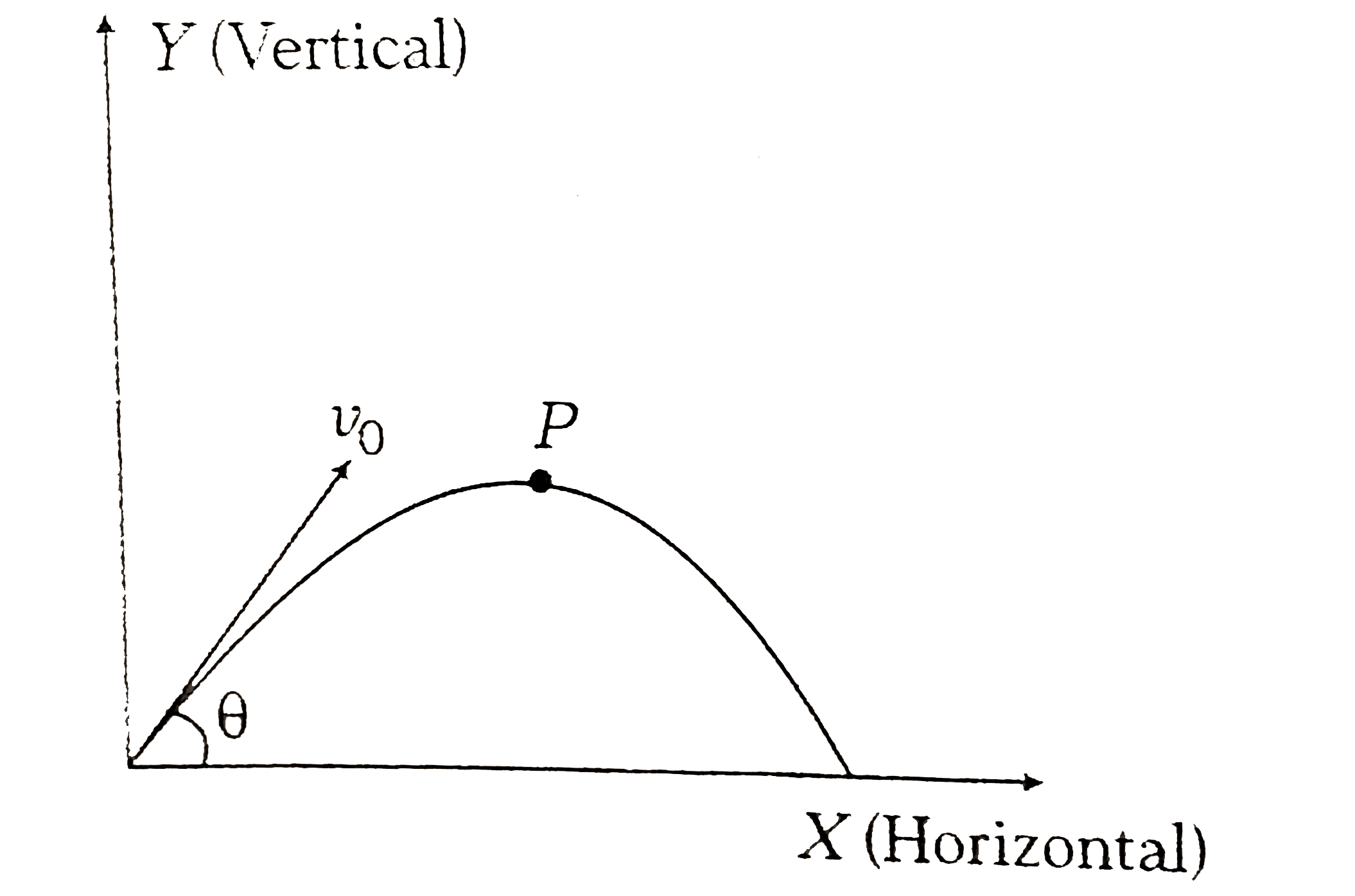
View SolutionIf a body of mass 200 g falls a height 200 m and its total P.E. is converted into K.E. at the point of contact of the body with earth surface. Then what is the decrease in P.E. of the body at the contact.
(g=10m/s2)
View SolutionFind the derivative of ex(x2+1) w.r.t. x
View SolutionAn object has velocity →v1 w.r.t. ground. An observer moving with constant velocity →v0 w.r.t. ground measures the velocity of the object as →v2. The magnitudes of three velocities are related by
View SolutionThe ratio of the speed of a projectile at the point of projection to the speed at the top of its trajectory is x. The angle of projection with the horizontal is
View SolutionA light container having a diatomic gas enclosed within is moving with velocity V. Mass of the gas is M and number of moles is n.
(i) What is the kinetic energy of gas w.r.t. centre of mass of the system?
(ii) What is K.E. of gas w.r.t. ground?
View Solution
