Assertion: In case of projectile motion, acceleration horizontal component of velocity and mechanical energy remains unchanged but speed. Vertical component of velocity, momentum K.E. and P.E. change.
Reason: In the presence of air resistance, the range and maximum height attained reduce, but time of flight increases.
both assertion & Reason are True & the Reason is a corrrect explanation of the Asserion.
If both Assertion & Reason are True but Reason is not correct explanation of the Assertion.
If Assertion is Trie but the Reason is False.
If both Assertion & Reason are false
The correct Answer is:B
To analyze the given assertion and reason, we will break down the concepts of projectile motion and the effects of air resistance step by step.
Step 1: Understanding Projectile Motion
In projectile motion, an object is launched at an angle with an initial velocity. The motion can be separated into horizontal and vertical components:
- Horizontal Component (x-direction):
- Initial velocity: Vx=Vcos(θ)
- Acceleration: ax=0 (no horizontal forces acting)
- Therefore, horizontal velocity remains constant: Vx=Vcos(θ)
- Vertical Component (y-direction):
- Initial velocity: Vy=Vsin(θ)
- Acceleration: ay=−g (gravity acts downwards)
- Vertical velocity changes over time due to gravity.
Step 2: Analyzing the Assertion
The assertion states:
1. The horizontal component of velocity remains unchanged.
2. Mechanical energy remains unchanged.
3. Speed, vertical component of velocity, momentum, kinetic energy, and potential energy change.
Analysis:
- Horizontal Component of Velocity: True, as there is no horizontal acceleration.
- Mechanical Energy: In the absence of air resistance, mechanical energy (sum of kinetic and potential energy) remains constant because gravity is a conservative force.
- Vertical Component of Velocity: True, it changes due to the acceleration from gravity.
- Speed: True, as speed is the magnitude of velocity, which changes due to the changing vertical component.
- Momentum: True, as vertical momentum changes due to the force of gravity.
- Kinetic Energy (K.E.) and Potential Energy (P.E.): Both change as the projectile moves up and down.
Thus, the assertion is true.
Step 3: Analyzing the Reason
The reason states:
- In the presence of air resistance, the range and maximum height attained reduce, but the time of flight increases.
Analysis:
- Range and Maximum Height: True, air resistance opposes the motion, reducing both the range and maximum height.
- Time of Flight: This part is false. Air resistance actually decreases the time of flight because it slows down the ascent and descent, leading to a shorter overall flight time.
Conclusion
- Assertion: True
- Reason: False
Final Answer
The assertion is true, but the reason is false.
In projectile motion, an object is launched at an angle with an initial velocity. The motion can be separated into horizontal and vertical components:
- Horizontal Component (x-direction):
- Initial velocity: Vx=Vcos(θ)
- Acceleration: ax=0 (no horizontal forces acting)
- Therefore, horizontal velocity remains constant: Vx=Vcos(θ)
- Initial velocity: Vy=Vsin(θ)
- Acceleration: ay=−g (gravity acts downwards)
- Vertical velocity changes over time due to gravity.
The assertion states:
1. The horizontal component of velocity remains unchanged.
2. Mechanical energy remains unchanged.
3. Speed, vertical component of velocity, momentum, kinetic energy, and potential energy change.
- Horizontal Component of Velocity: True, as there is no horizontal acceleration.
- Mechanical Energy: In the absence of air resistance, mechanical energy (sum of kinetic and potential energy) remains constant because gravity is a conservative force.
- Vertical Component of Velocity: True, it changes due to the acceleration from gravity.
- Speed: True, as speed is the magnitude of velocity, which changes due to the changing vertical component.
- Momentum: True, as vertical momentum changes due to the force of gravity.
- Kinetic Energy (K.E.) and Potential Energy (P.E.): Both change as the projectile moves up and down.
The reason states:
- In the presence of air resistance, the range and maximum height attained reduce, but the time of flight increases.
- Range and Maximum Height: True, air resistance opposes the motion, reducing both the range and maximum height.
- Time of Flight: This part is false. Air resistance actually decreases the time of flight because it slows down the ascent and descent, leading to a shorter overall flight time.
- Assertion: True
- Reason: False
The assertion is true, but the reason is false.
Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-2
170 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
Projectile motion is a combination of two one-dimensional motion: one in horizontal and other in vertical direction. Motion in 2D means in a plane. Necessary condition for 2D motion is that the velocity vector is coplanar to the acceleration vector. In case of projectile motion, the angle between velocity and acceleration will be 0∘<θ<180∘. During the projectile motion, the horizontal component of velocity ramains unchanged but the vertical component of velocity is time dependent. Now answer the following questions:
A body is projected at angle of 30∘ and 60∘ with the same velocity. Their horizontal ranges are R1 and R2 and maximum heights are H1andH2, respectively, then
A body is projected at angle of 30∘ and 60∘ with the same velocity. Their horizontal ranges are R1 and R2 and maximum heights are H1 and H2, respectively, then
View SolutionProjectile motion is a combination of two one-dimensional motion: one in horizontal and other in vertical direction. Motion in 2D means in a plane. Necessary condition for 2D motion is that the velocity vector is coplanar to the acceleration vector. In case of projectile motion, the angle between velocity and acceleration will be 0∘ltθlt180∘. During the projectile motion, the horizontal component of velocity ramains unchanged but the vertical component of velocity is time dependent. Now answer the following questions:
An object is projected from origin in x-y plane in which velocity changes according to relation →v=aˆi+bxˆj. Path of particle is
View SolutionProjectile motion is a combination of two one-dimensional motion: one in horizontal and other in vertical direction. Motion in 2D means in a plane. Necessary condition for 2D motion is that the velocity vector is coplanar to the acceleration vector. In case of projectile motion, the angle between velocity and acceleration will be 0∘<θ<180∘. During the projectile motion, the horizontal component of velocity ramains unchanged but the vertical component of velocity is time dependent. Now answer the following questions:
A particle is projected from the origin in the x-y plane. The acceleration of particle in negative y-direction is α. If equation of path of the particle is y=ax−bx2, then initial velocity of the particle is
View SolutionAn aeroplane takes off at an angle of 60∘ to the horizontal.If the velocity of the plane is 200kmh−1,calculate its horizontal and vertical component of its velocity.
View SolutionAssertion: In projectile motion horizontal velocity remains same but vertical velocity continously change Reason: particle strikes the ground with same vertical velocity with which the particle was thrwon in vertical direction.
View SolutionGiven that ux= horizontal component of initial velocity of a projectile, uy= vertical component of initial velocity, R= horizontal range, T = time of flight and H = maximum height of projectile. Now match the following two columns.

View SolutionA ball is projected on a very long floor. There may be two conditions (i) floor is smooth &(ii) the collision is elastic
If both the considered then the path of ball is as follows.

Now if collision is inelastic and surface is rough then the path is as follows.
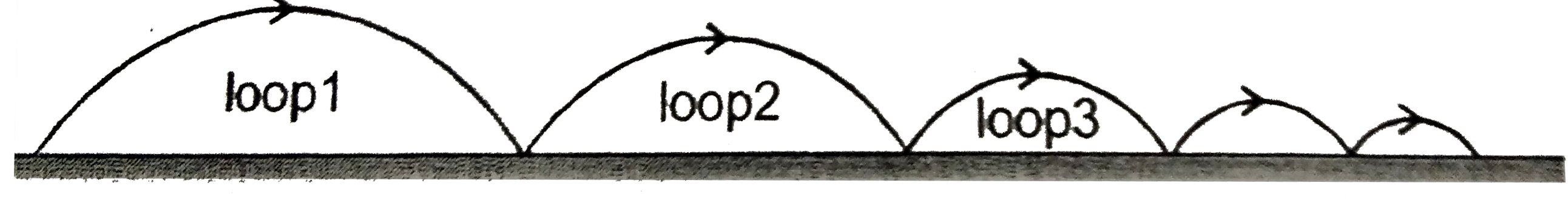
Successive range is decreasing .
Roughness of surface decreases the horizontal component of ball during collision and inelastic nature of collision decreases the vertical component of velocity of ball. In first case both components remain unchanged in magnitude and in second case both the components of the velocity will change.
Let us consider a third case here surface is rough but the collision of ball with floor is elastic. A ball is projected withe speed u at an angle 30∘ with horizontal and it is known that after collision with the floor its speed becomes u√3 . Then answer the following questions.
The ratio of maximum height reached by ball in first loop and second loop (H1H2) is :
View SolutionA ball is projected on a very long floor. There may be two conditions (i) floor is smooth &(ii) the collision is elastic
If both the considered then the path of ball is as follows.

Now if collision is inelastic and surface is rough then the path is as follows.

Successive range is decreasing .
Roughness of surface decreases the horizontal component of ball during collision and inelastic nature of collision decreases the vertical component of velocity of ball. In first case both components remain unchanged in magnitude and in second case both the components of the velocity will change.
Let us consider a third case here surface is rough but the collision of ball with floor is elastic. A ball is projected withe speed u at an angle 30∘ with horizontal and it is known that after collision with the floor its speed becomes u√3 . Then answer the following questions.
The angle made by the resultant velocity vector of the ball with horizontal after first collision with floor is :
View SolutionA ball is projected on a very long floor. There may be two conditions (i) floor is smooth &(ii) the collision is elastic
If both the considered then the path of ball is as follows.

Now if collision is inelastic and surface is rough then the path is as follows.

Successive range is decreasing .
Roughness of surface decreases the horizontal component of ball during collision and inelastic nature of collision decreases the vertical component of velocity of ball. In first case both components remain unchanged in magnitude and in second case both the components of the velocity will change.
Let us consider a third case here surface is rough but the collision of ball with floor is elastic. A ball is projected withe speed u at an angle 30∘ with horizontal and it is known that after collision with the floor its speed becomes u√3 . Then answer the following questions.
If the ball after first collision with the floor has rebounded vertically then the speed of the ball just after the collision with the floor would have been :
View SolutionAssertion : Two projectile have maximum heights 4H and H respectively. The ratio of their horizontal components of velocities should be 1:2 for their horizontal ranges to be same.
Reason : Horizontal range = horizontal component of velocity xx time of flight.
View Solution
