Assertion: To cross the river in minimum time swimmer should swimming in perpendicular direction to the water current.
Reason: In this case river flow helps to cross this river.
If both assertion & Reason are True & the Reason is a corrrect explanation of the Asserion.
If both Assertion & Reason are True but Reason is not correct explanation of the Assertion.
If Assertion is Trie but the Reason is False.
If both Assertion & Reason are false
The correct Answer is:C
To solve the assertion and reason question regarding the swimmer crossing a river, we will break down the concepts involved step by step.
Step 1: Understanding the Assertion
The assertion states that to cross the river in minimum time, the swimmer should swim in a direction perpendicular to the water current. This means that if the river flows horizontally (let's say in the x-direction), the swimmer should aim to swim straight across (in the y-direction).
Hint: Think about the direction of the swimmer's velocity relative to the river's current.
Step 2: Analyzing the Reason
The reason given is that the river flow helps to cross the river. However, we need to analyze whether this statement is true. The swimmer's goal is to minimize the time taken to cross the river, and swimming perpendicular to the current does not mean that the current assists in crossing; rather, it affects the swimmer's path.
Hint: Consider how the current affects the swimmer's trajectory and whether it aids in crossing directly.
Step 3: Evaluating the Time Taken to Cross
To determine the time taken to cross the river, we can use the formula for time, which is distance divided by velocity. The distance to cross the river is 'd', and the effective velocity of the swimmer in the y-direction (perpendicular to the current) is 'Vy'. Therefore, the time taken to cross the river is given by:
Time=dVy
Hint: Remember that the swimmer's speed in the y-direction is crucial for minimizing time.
Step 4: Understanding the Role of River Flow
The river flow does not help the swimmer cross the river directly; instead, it carries the swimmer downstream while they are swimming across. The swimmer's effective velocity is a combination of their swimming speed and the river's current, but the current does not contribute to the crossing speed.
Hint: Think about the vector components of the swimmer's velocity and how they relate to the river's current.
Step 5: Conclusion
Based on the analysis:
- The assertion is true: swimming perpendicular to the current does indeed minimize the time taken to cross the river.
- The reason is false: the river flow does not help in crossing; it merely affects the swimmer's path.
Thus, the correct conclusion is that the assertion is true, and the reason is false.
Final Answer: Assertion is true, Reason is false.
The assertion states that to cross the river in minimum time, the swimmer should swim in a direction perpendicular to the water current. This means that if the river flows horizontally (let's say in the x-direction), the swimmer should aim to swim straight across (in the y-direction).
The reason given is that the river flow helps to cross the river. However, we need to analyze whether this statement is true. The swimmer's goal is to minimize the time taken to cross the river, and swimming perpendicular to the current does not mean that the current assists in crossing; rather, it affects the swimmer's path.
To determine the time taken to cross the river, we can use the formula for time, which is distance divided by velocity. The distance to cross the river is 'd', and the effective velocity of the swimmer in the y-direction (perpendicular to the current) is 'Vy'. Therefore, the time taken to cross the river is given by:
The river flow does not help the swimmer cross the river directly; instead, it carries the swimmer downstream while they are swimming across. The swimmer's effective velocity is a combination of their swimming speed and the river's current, but the current does not contribute to the crossing speed.
Based on the analysis:
- The assertion is true: swimming perpendicular to the current does indeed minimize the time taken to cross the river.
- The reason is false: the river flow does not help in crossing; it merely affects the swimmer's path.
Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-2
170 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
Assertion: Separation between two bodies moving in the same direction on the ground with same acceleration, will not increase.
Reason: In this case river flow helps to cross the river.
View Solution(A): A man is on the northern bank of a river. To cross the river in a shortest time he should swim due south.
(R) : Man should move opposite to the river flow to cross in shortest time.
View SolutionTo cross the river in shortest distance, a swimmer should swimming an angle θ with the upsteram. What is the ratio of the time taken to swim across in the shortest time to that in swimming across over shortest distance. [Asume that the speed of swimmer in still water is greater than the speed of river flow]
View SolutionA boat 'B' is moving upstream with velocity 3m/s with respect to ground. An observer standing on the boat observes that a swimmer 'S' is crossing the river perpendicular to the direction of motion of the boat. If river flow velocity is 4m/s and swimmer crosses the river of width 100,m is 50s. Then
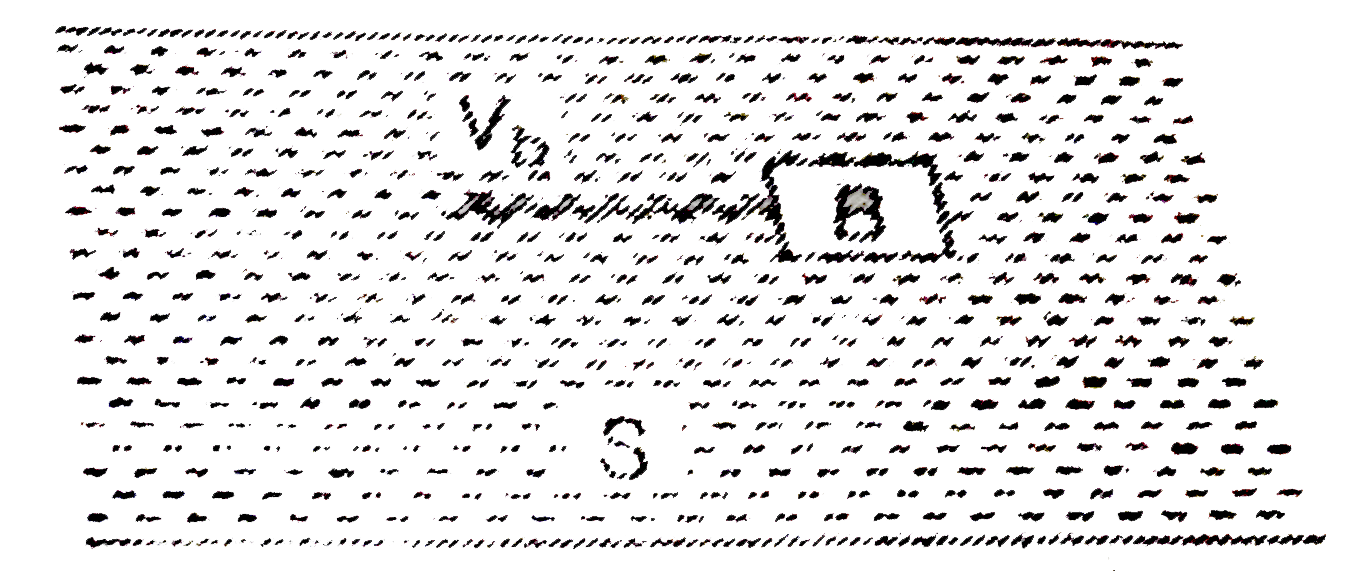
View SolutionA man swims across a river with speed of Vm perpendicular to the flow direction of river. If the water flows with a speed Vw with what resullant velocity does the man cross the river ?
View SolutionThe width of a river is 3√3 km. A boat has a velocity of √3 km/s and starts to cross the river in a direction perpendicular to the bank of the river. If the river is flowing with a velocity 2km/sec, find the distance drifted by the boat.
View SolutionA boat can be rowed at 5 m/s on still water. It is used to cross a 200m wide river from the south bank to the north bank. The river current has uniform velocity of 3 m/s due east.
(a) In which direction must it be steered to cross the river perpendicular to current ?
(b) How long will it take to cross the river in a direction perpendicular to the river flow ?
(c) In which direction must the boat be steered to cross the river in minimum time ? How far will it drift ?
View SolutionThe river 500 m wide is flowing with a current of 4kph. A boat starts from one bank of the river wishes to cross the river at right angle to stream direction. Boatman can row the boat at 8 kph. In which direction he should row the boat. What time he ''ll take to cross the river ?
View SolutionVelocity of the river with respect to ground is given by v0. Width of the river is d. A swimmer swims (with respect to water) perpendicular to the current with acceleration a=2t (where t is time) starting from rest from the origin O at t=0. The equation of trajectory of the path followed by the swimmer is

View SolutionA river of width 100 m is flowing with a velocity of 1.5 m/s. A man start from one end with rest relative the river. He raws with an acceleration of 2m/s2 relative to the river. If the man want to cross the river in minimum time, by how much distance (in meters) will he be drifted (flown) in the direction of river flow during the crossing.
View Solution
