The equivalent resistance of two resistor connected in series is 6Ω and their equivalent resistance is 43Ω. What are the values of resistances ?
4Ω,6Ω
8Ω,1Ω
4Ω,2Ω
6Ω,2Ω
The correct Answer is:C
To solve the problem of finding the values of two resistors R1 and R2 given their equivalent resistance in series and parallel, we can follow these steps:
Step 1: Write down the equations for series and parallel resistances.
For resistors in series:
Rs=R1+R2
Given that Rs=6Ω, we have:
R1+R2=6(Equation 1)
For resistors in parallel:
Rp=R1R2R1+R2
Given that Rp=43Ω, we can substitute R1+R2 from Equation 1:
R1R26=43
Multiplying both sides by 6 gives:
R1R2=8(Equation 2)
Step 2: Solve the system of equations.
Now we have two equations:
1. R1+R2=6
2. R1R2=8
From Equation 1, we can express R2 in terms of R1:
R2=6−R1
Step 3: Substitute R2 into Equation 2.
Substituting R2 into Equation 2:
R1(6−R1)=8
Expanding this gives:
6R1−R21=8
Rearranging the equation:
R21−6R1+8=0
Step 4: Solve the quadratic equation.
We can solve this quadratic equation using the quadratic formula:
R1=−b±√b2−4ac2a
where a=1,b=−6,c=8:
R1=6±√(−6)2−4⋅1⋅82⋅1
R1=6±√36−322
R1=6±√42
R1=6±22
This gives us two possible values:
R1=82=4orR1=42=2
Step 5: Find R2.
Using R1=4:
R2=6−R1=6−4=2
Using R1=2:
R2=6−R1=6−2=4
Conclusion:
Thus, the values of the resistances are:
R1=4ΩandR2=2Ω
Final Answer:
The resistances are 4Ω and 2Ω.
---
For resistors in series:
Rs=R1+R2
Given that Rs=6Ω, we have:
R1+R2=6(Equation 1)
Rp=R1R2R1+R2
Given that Rp=43Ω, we can substitute R1+R2 from Equation 1:
R1R26=43
Multiplying both sides by 6 gives:
R1R2=8(Equation 2)
Now we have two equations:
1. R1+R2=6
2. R1R2=8
R2=6−R1
Substituting R2 into Equation 2:
R1(6−R1)=8
Expanding this gives:
6R1−R21=8
Rearranging the equation:
R21−6R1+8=0
We can solve this quadratic equation using the quadratic formula:
R1=−b±√b2−4ac2a
where a=1,b=−6,c=8:
R1=6±√(−6)2−4⋅1⋅82⋅1
R1=6±√36−322
R1=6±√42
R1=6±22
This gives us two possible values:
R1=82=4orR1=42=2
Using R1=4:
R2=6−R1=6−4=2
Using R1=2:
R2=6−R1=6−2=4
Thus, the values of the resistances are:
R1=4ΩandR2=2Ω
The resistances are 4Ω and 2Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Knowledge Check
The correct combination of three resistances 1Ω,2Ωand3Ω to get equivalent resistance 115Ω is
AAll three are combines in paralleBAll three are combines in paralleC1Ωand2Ω in parallel and 3Ω is in series to bothD2Ωand3Ω in parallel and 3Ω is in series to both
Two resistors having resistance 4 Ω and 6 Ω are connected in parallel. Find their equivalent resistance.
View SolutionThese resistors of 10Ω,15Ωand5Ω are connected in parallel. Find their equivalent resistance.
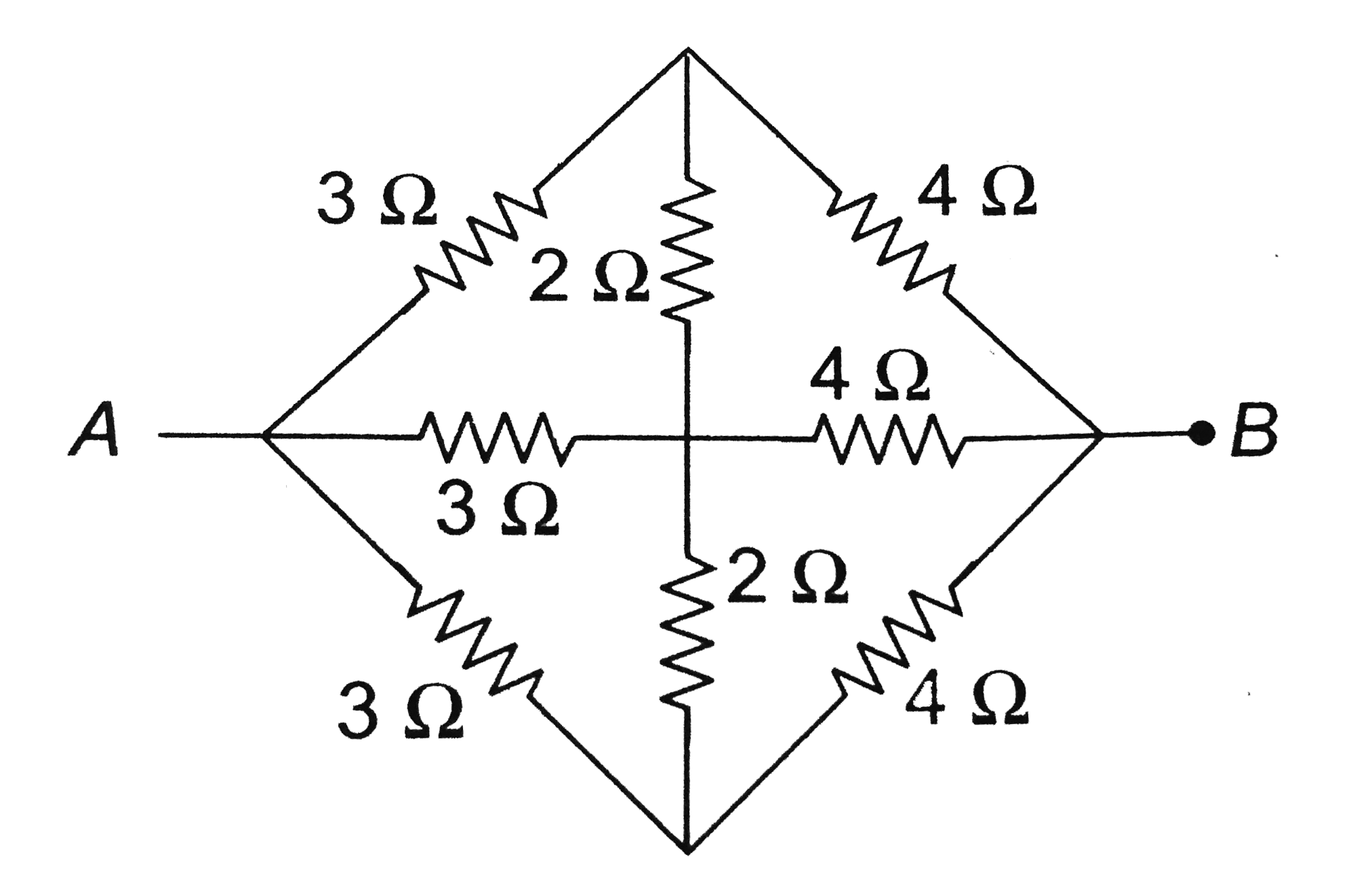
View SolutionThe equivalent resistance between A and B will be (in Ω)
View SolutionThe resultant resistance of two resistance in series is 50 Ω and it is 12 Ω , when they are in parallel. The individual resistances are
View SolutionA carbon and an aluminium wire are connected in series. If the combination has equivalent resistance of(90Ω) at (0∘C), the value of the resistance of each wire at(0∘C) so that the resistance of combination does not change with temperature is
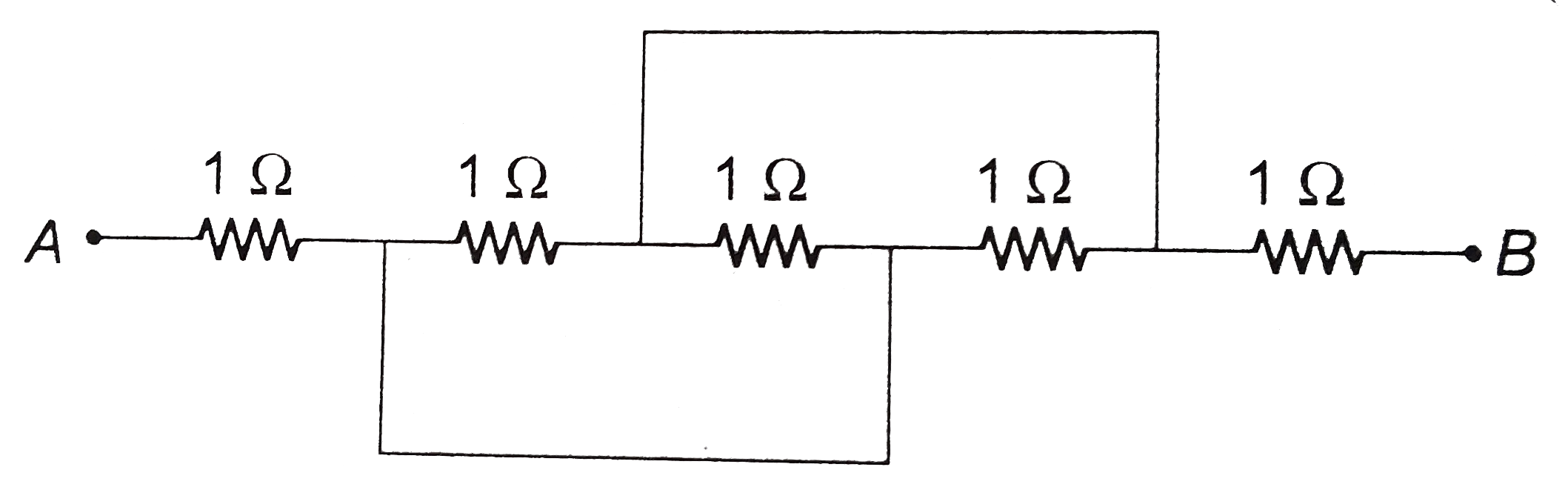
View SolutionEquivalent resistance between the points A and B (in Ω)
 .
.
View SolutionMinimum resistance obtained from two resistors 3Ω and 2Ω is
View Solution