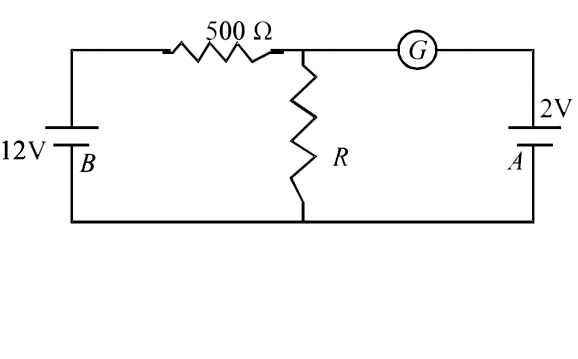
In the following circuit diagram. The galvanometer reading is zero. If the inter nal resistance of cells are negligible then what is the value of X?
To solve the problem, we will use Kirchhoff's Voltage Law (KVL) and the information provided about the circuit. Here’s a step-by-step solution:
Step 1: Understand the Circuit
We have a circuit with two voltage sources (12V and 2V) and a resistor of 500 ohms. The galvanometer reading is zero, indicating that the current through the galvanometer is zero. This means the potential difference across the galvanometer is also zero.
Step 2: Apply Kirchhoff's Voltage Law (KVL)
According to KVL, the sum of the potential differences in a closed loop is equal to zero. For the outer loop of the circuit, we can write the equation as:
12V−2V−500I=0
Step 3: Simplify the KVL Equation
Rearranging the equation gives us:
12V−2V=500I
10V=500I
Step 4: Solve for Current (I)
Now, we can solve for the current I:
I=10V500Ω
I=150 A
Step 5: Use the Galvanometer Reading
Since the galvanometer reading is zero, the potential across the resistor X must equal the potential difference of the 2V source. The potential across the resistor X can be expressed as:
VX=I⋅X
Setting this equal to 2V gives:
I⋅X=2V
Step 6: Substitute the Value of I
Substituting I=150 into the equation:
150⋅X=2
Step 7: Solve for X
Now, we can solve for X:
X=2⋅50
X=100Ω
Conclusion
The value of the resistor X is 100Ω.
---
We have a circuit with two voltage sources (12V and 2V) and a resistor of 500 ohms. The galvanometer reading is zero, indicating that the current through the galvanometer is zero. This means the potential difference across the galvanometer is also zero.
According to KVL, the sum of the potential differences in a closed loop is equal to zero. For the outer loop of the circuit, we can write the equation as:
12V−2V−500I=0
Rearranging the equation gives us:
12V−2V=500I
10V=500I
Now, we can solve for the current I:
I=10V500Ω
I=150 A
Since the galvanometer reading is zero, the potential across the resistor X must equal the potential difference of the 2V source. The potential across the resistor X can be expressed as:
VX=I⋅X
Setting this equal to 2V gives:
I⋅X=2V
Substituting I=150 into the equation:
150⋅X=2
Now, we can solve for X:
X=2⋅50
X=100Ω
The value of the resistor X is 100Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-III
26 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV A
32 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
Similar Questions
If internal resistance of cell is negligible, then current flowing through the circuit is
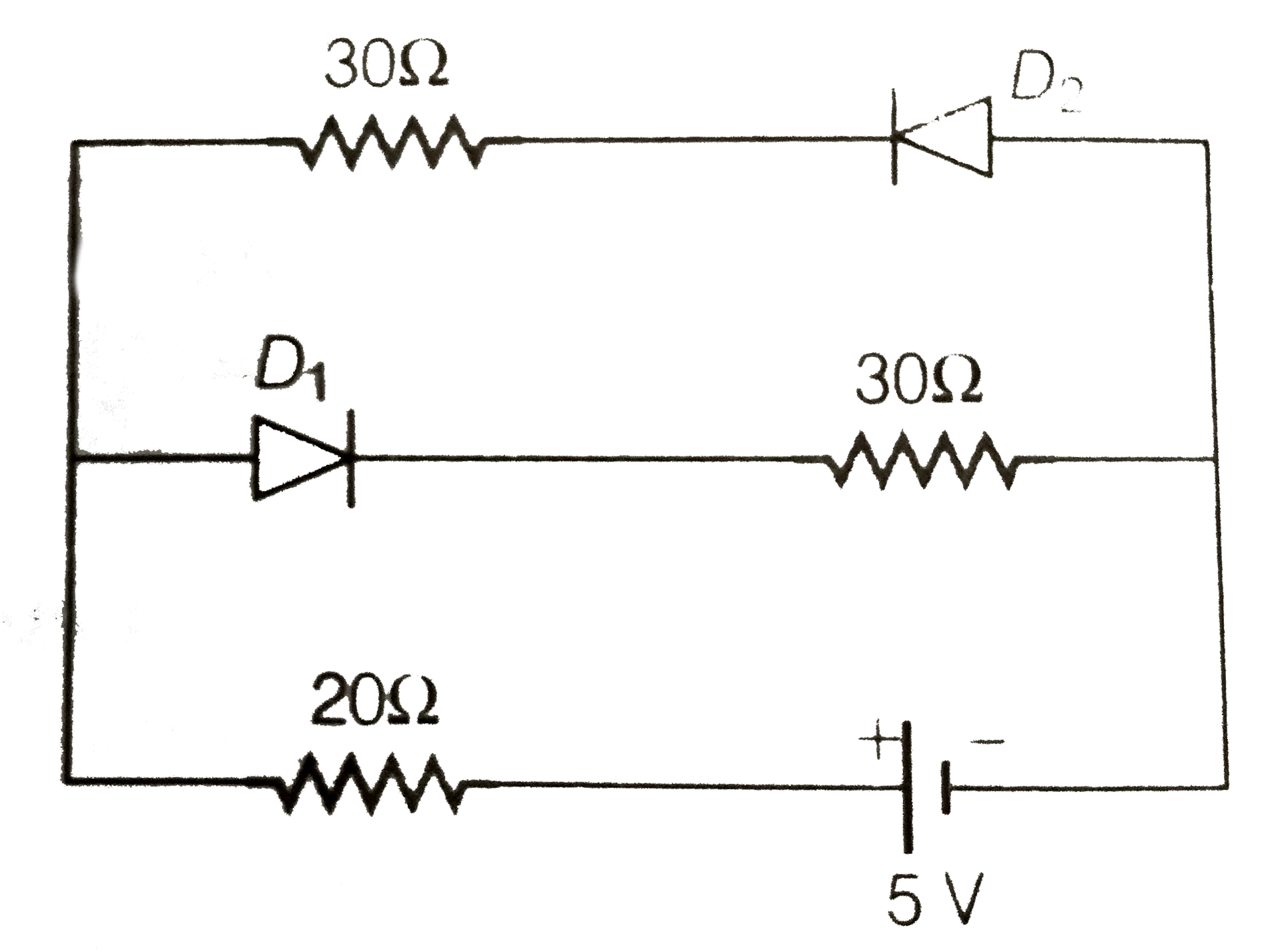
View SolutionThe reading of a galvanometer connected in the circuit is zero. If the internal resistance of a battery is zero then find the value of X.

View SolutionFor the following diagram the galvanometer shows zero deflection then what is the value of R?
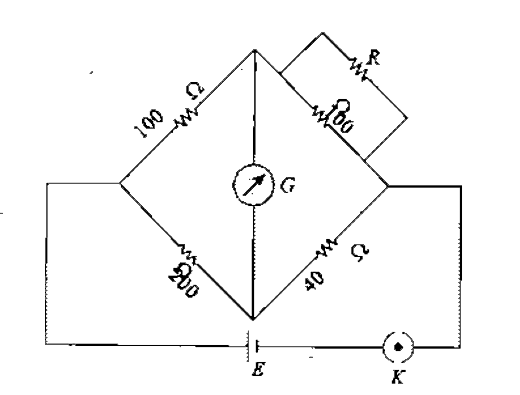
View SolutionIn the circuit, the galvanometer G shows zero deflection. If the batteries A and b have negligible internal resistance, the value of the resistor R will be -
View SolutionDraw a circuit diagram for the determination of the internal resistance of a cell using potentiometer. Derive the formula to be used.
View SolutionIn the circuit shown, the galvanometer shows zero current. The value of resistance R is :
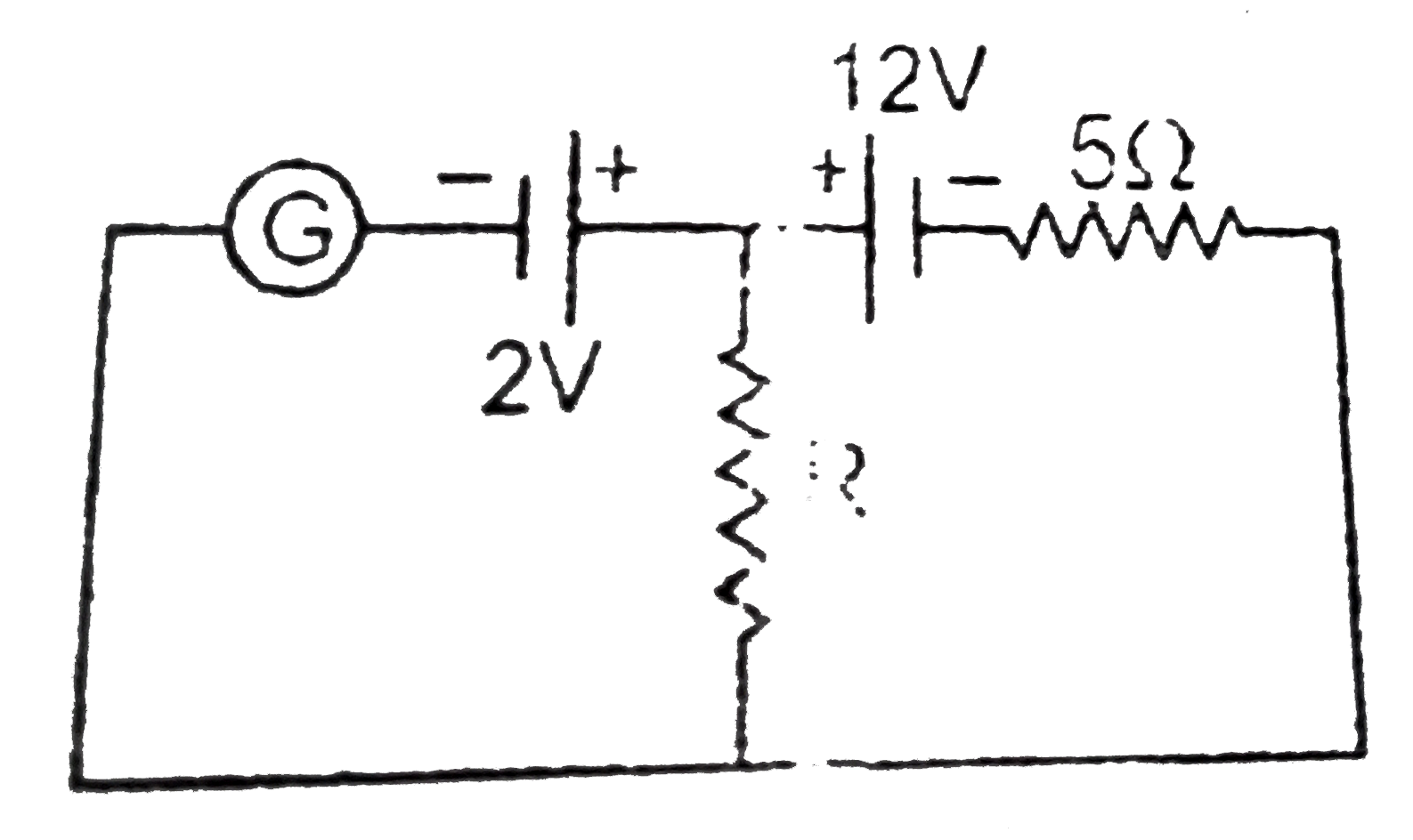
View SolutionIn the circuit shown, the galvanometer shows zero current. The value of resistance R is :

View SolutionIn the following circuit diagram the value of resistance X for the potential difference between B and D is zero:-

View SolutionIn a circuit shown in figure if the internal resistances of the sources are negligible then at what value of resistance R will the thermal power generated in it will be the maximum. What is the value of maximum power?
View SolutionIn the circuit shown , the internal resistance of the cell is negligible . The steady stale current in the 2Ω resistor is
View Solution
