The resistance of an ammeter of range 5A is 1.8Ω A shunt of 0.2Ω is connected in parallel to it. When its indicator shows a current of 2A then what will be effective current?
The linear mass density continuously decreases from left to right.
The linear mass density continuously increases from left to right.
The linear mass density decreases from left to fight upto centre and then increases.
The linear mass density increases from left to right upto cente and then decreases.
The correct Answer is:(CD)
To solve the problem step by step, we will follow these calculations:
Step 1: Identify the given values
- Resistance of the ammeter (R) = 1.8 Ω
- Resistance of the shunt (R_shunt) = 0.2 Ω
- Current shown by the ammeter (I) = 2 A
Step 2: Calculate the voltage across the ammeter
Using Ohm's Law, we can calculate the voltage across the ammeter when it shows a current of 2 A:
V=I×R
V=2A×1.8Ω=3.6V
Step 3: Determine the current through the shunt
The voltage across the shunt is the same as the voltage across the ammeter, which is 3.6 V. Now, we can calculate the current through the shunt (I_shunt) using Ohm's Law:
Ishunt=VRshunt
Ishunt=3.6V0.2Ω=18A
Step 4: Calculate the effective current
The effective current (I_E) in the circuit is the sum of the current through the ammeter and the current through the shunt:
IE=I+Ishunt
IE=2A+18A=20A
Final Answer
The effective current is 20 A.
---
- Resistance of the ammeter (R) = 1.8 Ω
- Resistance of the shunt (R_shunt) = 0.2 Ω
- Current shown by the ammeter (I) = 2 A
Using Ohm's Law, we can calculate the voltage across the ammeter when it shows a current of 2 A:
V=2A×1.8Ω=3.6V
The voltage across the shunt is the same as the voltage across the ammeter, which is 3.6 V. Now, we can calculate the current through the shunt (I_shunt) using Ohm's Law:
Ishunt=3.6V0.2Ω=18A
The effective current (I_E) in the circuit is the sum of the current through the ammeter and the current through the shunt:
IE=2A+18A=20A
The effective current is 20 A.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-III26videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV A32videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)6videos
CIRCULAR MOTION
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective14videos
GEOMETRICAL OPTICS
Similar Questions
The resistance of galvanometer is 999Ω. A shunt of 1Ω is connected to it. If the main current is 10−2A, what is the current flowing through the galvanometer.
View SolutionThe ammeter shown in figure consists of a 480Ω coil connected in parallel to 20Ω shunt. Find the reading of the ammeter
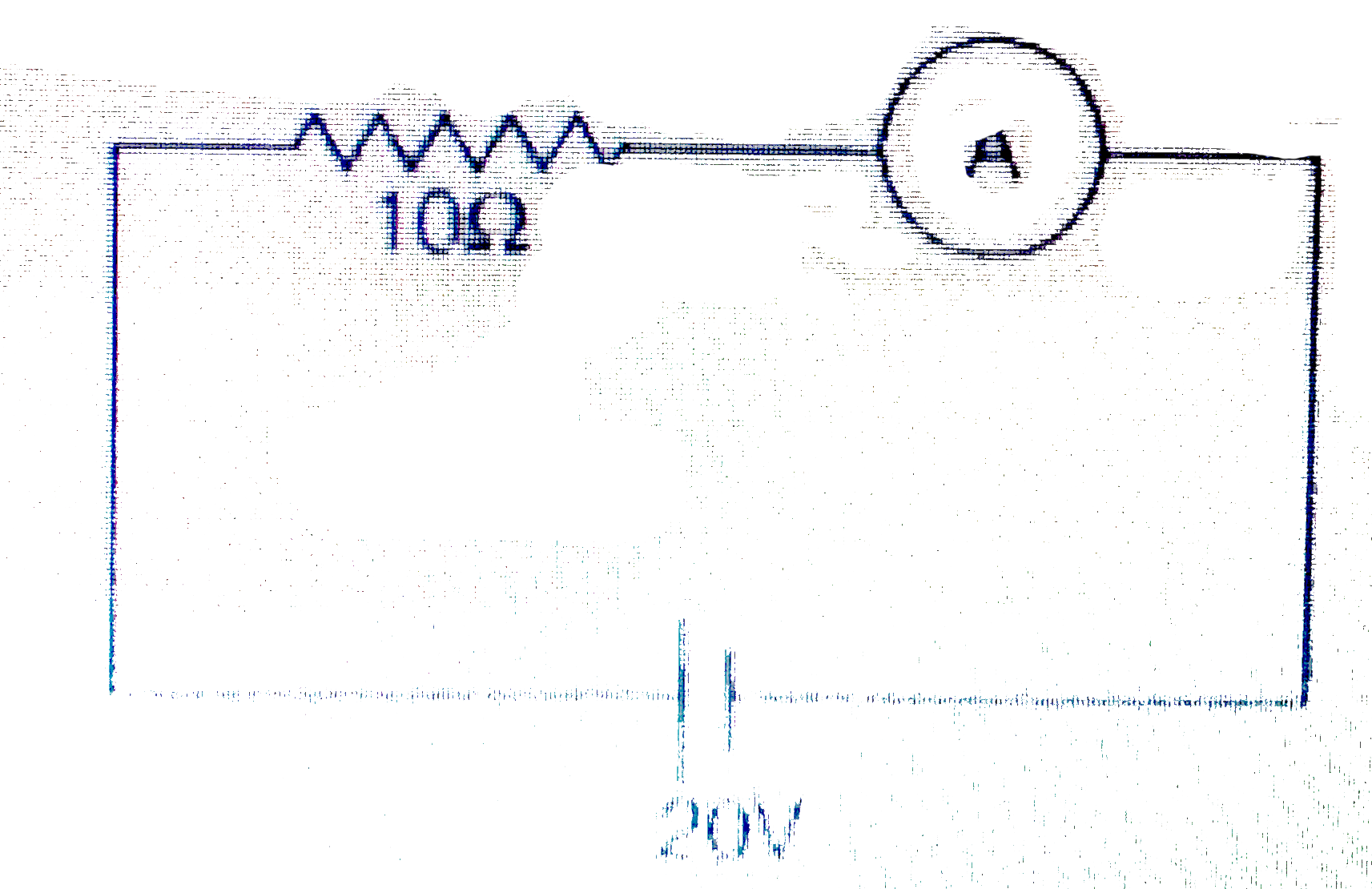 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If the galvanometer current is 10 mA, resistance of the galvanometer is 40Ω and shunt of 2Ω is connected to the galvanometer, the maximum current which can be measured by this ammeter is
A0.21AB2.1AC210AD21A
Resistance of a Galvanometer coil is 8Ω and 2Ω Shunt resistance is connected with it. If main current is 1 A then the current flow through 2Ω resistance will be :
View SolutionThe ammeter shown in figure consists of a480(ω)coil connected in parallel to a20(ω) shunt. Find the reading of the ammeter.
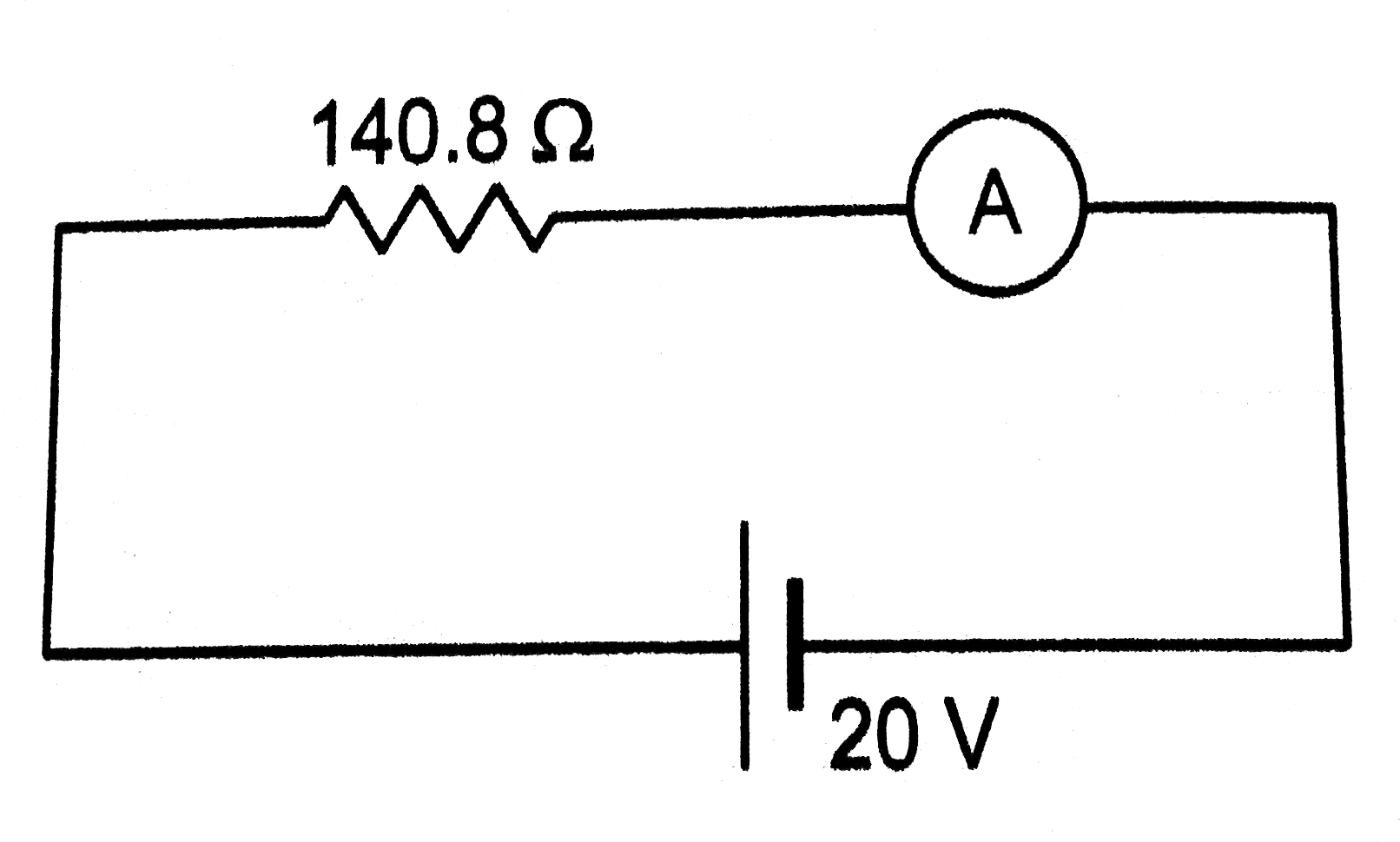 View Solution
View SolutionThe deflection of a galvanometer falls to 1/10th when a resistance of 5Ω is connected in parallel with it. If an additional resistance of 2Ω is connected in parallel to the galvanometer, the deflection is
View SolutionTwo cells of 1.5 V and 2 V , having internal resistances of 1Ω and 2Ω respectively, are connected in parallel so as to read the current in the same direction through an external resistance of 5Ω . The current in the external resistance will be
View SolutionThe Total resistance when connected in series in 9Ω and when connected in parallel is 2Ω The value of two resistance are
View SolutionThree resistances 2Ω,3Ω and 4Ω are connected in parallel. The ratio of currents passing through them when a potential difference is applied across its ends will be
View SolutionTwo resistors of resistances 2Ω and 6Ω are connected in parallel. This combination is then connected to a battery of emf 2 V and internal resistance 0.5Ω. What is the current flowing through the battery ?
View Solution

