There is a definite potential difference between the two ends of a potentiometer. Two cells are connected in such a way that first time help each other, and second time they oppose each other. They are balanced on the potentiometer wire at 120cm and 60cm length respectively. compare the electromotive force of the cells. potentiometer wire at 120cm and 60cm length respectively. Compare the electromotive force of the cells.
53∘
37∘
45∘
30∘
The correct Answer is:(B)
To solve the problem of comparing the electromotive forces (emf) of two cells connected in a potentiometer, we can follow these steps:
1. Understand the Setup:
- We have a potentiometer wire with a potential difference across it.
- Two cells are connected in two different configurations:
- In the first configuration, they help each other (E1 + E2).
- In the second configuration, they oppose each other (E1 - E2).
2. Establish the Relationships:
- The potential gradient (k) of the potentiometer wire relates the emf (E) and the length (l) of the wire:
E=k⋅l
3. Write the Equations:
- For the first configuration (helping each other), the length of the wire is 120 cm:
E1+E2=k⋅120
- For the second configuration (opposing each other), the length of the wire is 60 cm:
E1−E2=k⋅60
4. Label the Equations:
- Let’s label the first equation as (1) and the second equation as (2):
- (1) E1+E2=k⋅120
- (2) E1−E2=k⋅60
5. Divide the Equations:
- Divide equation (1) by equation (2):
E1+E2E1−E2=k⋅120k⋅60
- The k cancels out:
E1+E2E1−E2=12060=2
6. Cross-Multiply:
- Cross-multiplying gives:
E1+E2=2(E1−E2)
7. Expand and Rearrange:
- Expanding the right side:
E1+E2=2E1−2E2
- Rearranging gives:
E1+E2+2E2=2E1
3E2=E1
8. Final Comparison:
- From the equation 3E2=E1, we can express the ratio of the emfs:
E1E2=31
Conclusion:
The ratio of the electromotive forces of the two cells is E1:E2=3:1.
---
- We have a potentiometer wire with a potential difference across it.
- Two cells are connected in two different configurations:
- In the first configuration, they help each other (E1 + E2).
- In the second configuration, they oppose each other (E1 - E2).
- The potential gradient (k) of the potentiometer wire relates the emf (E) and the length (l) of the wire:
E=k⋅l
- For the first configuration (helping each other), the length of the wire is 120 cm:
E1+E2=k⋅120
- For the second configuration (opposing each other), the length of the wire is 60 cm:
E1−E2=k⋅60
- Let’s label the first equation as (1) and the second equation as (2):
- (1) E1+E2=k⋅120
- (2) E1−E2=k⋅60
- Divide equation (1) by equation (2):
E1+E2E1−E2=k⋅120k⋅60
- The k cancels out:
E1+E2E1−E2=12060=2
- Cross-multiplying gives:
E1+E2=2(E1−E2)
- Expanding the right side:
E1+E2=2E1−2E2
- Rearranging gives:
E1+E2+2E2=2E1
3E2=E1
- From the equation 3E2=E1, we can express the ratio of the emfs:
E1E2=31
The ratio of the electromotive forces of the two cells is E1:E2=3:1.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-III26videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV A32videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)6videos
CIRCULAR MOTION
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective14videos
GEOMETRICAL OPTICS
Similar Questions
A potentiometer wire is 100cm long hand a constant potential difference is maintained across it. Two cells are connected in series first to support one another and then in opposite direction. The balance points are obatined at 50cm and 10cm from the positive end of the wire in the two cases. The ratio of emfs is:
View SolutionTwo cells of emfs E1 and E2 are connected together in two ways shown here. The 'balance points' in a given potentiometer experiment for these two combinations of cells are found to be at 351.0 cm and 70.2 cm respectively. Calculate the ratio of the emfs of the two cells.
 View Solution
View SolutionPotentiometer wire of length 1m is connected in series with 490Ω resistance and 2V battery. If 0.2mVcm is the potential gradient, then resistance of the potentiameter wire is approximately
View SolutionPotentiometer wire of length 1m is connected in series with 490Ω resistance and 2V battery. If 0.2mVcm is the potential gradient, then resistance of the potentiameter wire is approximately
View SolutionThe internal resistance of a cell is determined by using a potentiometer. In an experimetn, an external resistance of 60Ω is used across the given cell. When the key is closed, the balance length on the potentiometer decreases form 72 cm to 60 cm. calculate the internal resistance of the cell.
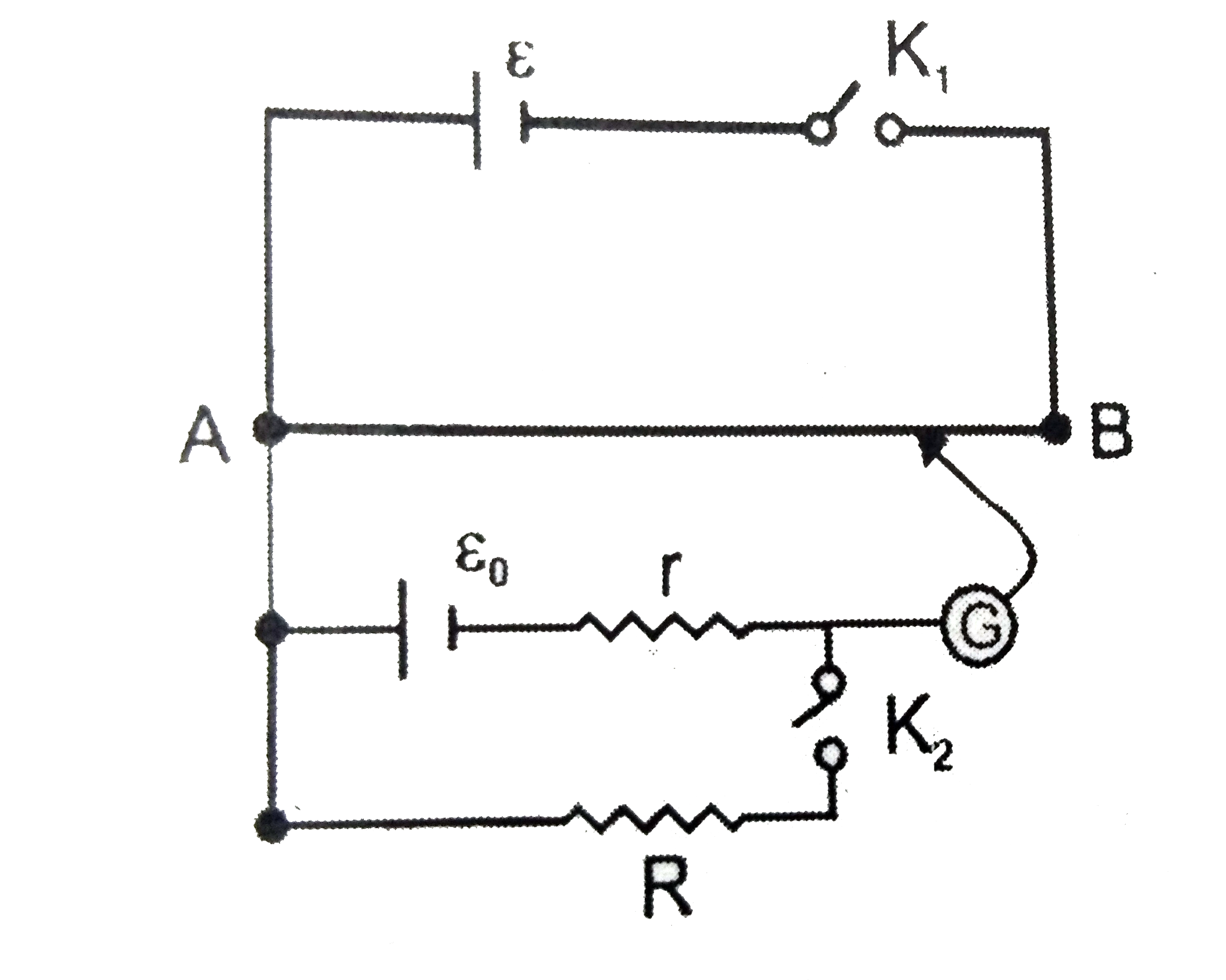 View Solution
View SolutionThe length of the potentiometer wire is 600 cm and a current of 40 mA is flowing in it. When a cell of emf 2 V and internal resistance 10Ω is balanced on this potentiometer the balance length is found to be 500 cm. The resistance of potentiometer wire will be
View SolutionThere is a potentiometer wire of length 1200 cm and 60 mA current is flowing in it. A battery of emf 5V and internal resistance of 20ohm is balanced on potentiometer wire with balancing length 1000 cm. The resistance of potentiometer wire is
View SolutionIn fig. battery E is balanced on 55cm length of potentiometer wire but when a resistance of 10Ω is connected in parallel with the battery then it balances on 50cm length of the potentiometer wire then internal resistance r of the battery is:-
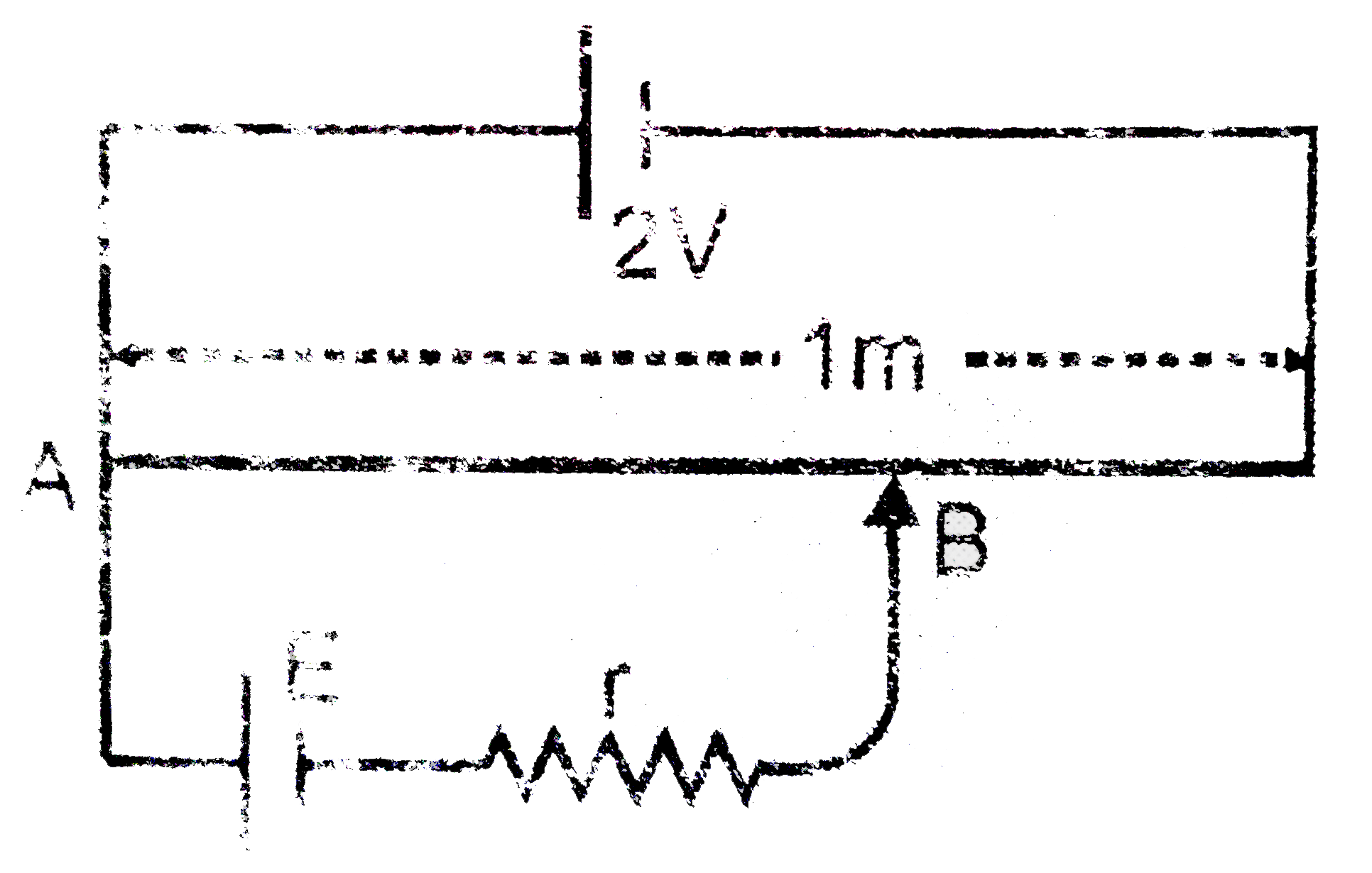 View Solution
View SolutionIn a potentiometer experiment, two cells connected in series get balanced at 9 m length of the wire. Now, if the connections of terminals of cell of lower emf are reversed, then the balancing length is obtained at 3 m. The ratio of emf's of two cells will be
View SolutionAN ideal battery of 4 V and resistance R are connected in series in the primary circuit of a potentiometer of length 1 m and and resistance 5Ω the value of R, to give a difference of 56mV across 10 cm of potentiometer wire , is :
View Solution

