Three resistance of values 2Ω,3Ω and 6Ω are to be connected to produce an effective resistance of 4Ω. This can be done by connecting.
6Ω resistance in series with the parallel combination of 2Ω and 3Ω
B3Ωresistance in series with the parallel combination of 2Ω and 6Ω
2Ωresistance in series with the parallel combination of 3Ω and 6Ω
2Ω resistance in parallel with the parallel combination of 3Ω and 6Ω
The correct Answer is:A
To find a way to connect three resistances (2Ω, 3Ω, and 6Ω) to achieve an effective resistance of 4Ω, we can follow these steps:
Step 1: Understand the Configuration
We need to determine how to connect the resistors. The effective resistance can be achieved by connecting some resistors in parallel and others in series.
Step 2: Connect 3Ω and 6Ω in Parallel
When resistors are connected in parallel, the formula for the equivalent resistance Req is given by:
1Req=1R1+1R2
For our case, let’s connect the 3Ω and 6Ω resistors in parallel.
Using the formula:
1Req=13+16
Step 3: Calculate the Equivalent Resistance of 3Ω and 6Ω
To calculate:
1Req=26+16=36=12
Thus:
Req=2Ω
Step 4: Connect the 2Ω Resistor in Series
Now, we will connect the equivalent resistance (2Ω) from the parallel connection with the 2Ω resistor in series. The formula for resistors in series is:
Rtotal=R1+R2
So, we have:
Rtotal=2Ω+2Ω=4Ω
Conclusion
By connecting the 3Ω and 6Ω resistors in parallel and then connecting the resulting 2Ω in series with the 2Ω resistor, we achieve an effective resistance of 4Ω.
Final Answer
The configuration to achieve an effective resistance of 4Ω is:
- Connect 3Ω and 6Ω in parallel.
- Connect the resulting equivalent resistance (2Ω) in series with the 2Ω resistor.
---
We need to determine how to connect the resistors. The effective resistance can be achieved by connecting some resistors in parallel and others in series.
When resistors are connected in parallel, the formula for the equivalent resistance Req is given by:
1Req=1R1+1R2
For our case, let’s connect the 3Ω and 6Ω resistors in parallel.
1Req=13+16
To calculate:
1Req=26+16=36=12
Thus:
Req=2Ω
Now, we will connect the equivalent resistance (2Ω) from the parallel connection with the 2Ω resistor in series. The formula for resistors in series is:
Rtotal=R1+R2
So, we have:
Rtotal=2Ω+2Ω=4Ω
By connecting the 3Ω and 6Ω resistors in parallel and then connecting the resulting 2Ω in series with the 2Ω resistor, we achieve an effective resistance of 4Ω.
The configuration to achieve an effective resistance of 4Ω is:
- Connect 3Ω and 6Ω in parallel.
- Connect the resulting equivalent resistance (2Ω) in series with the 2Ω resistor.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV A
32 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV B
14 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
Similar Questions
Three resistors of 2Ω,3Ω and 4Ω are connected in
series
View SolutionHow can three resistors of resistances 2Ω,3Ω, and 6Ω be connected to give a total resistance of
(a) 4Ω
(b) 1Ω ?
View SolutionThese resistors of 10Ω,15Ωand5Ω are connected in parallel. Find their equivalent resistance.
View SolutionThree resistors of 1Ω,2Ωand3Ω are connected in parallel. The combined resistance of 3 resistors should be
View SolutionIn Wheatstone bridge, four resistors of resistances 15Ω,12Ω,4Ω and 10Ω respectively, are connected in cyclic order. The resistance ( in Ω) that is to be connected in parallel with the resistance of 10Ω to balance the network is
View SolutionWhat resistance must be connected to a 15 Ω resistance to provide an effective resistance of 6Ω ?
View SolutionTwo resistors having resistance 4 Ω and 6 Ω are connected in parallel. Find their equivalent resistance.
View SolutionThe resistance of 0.1 N solution of acetic acid is 250 ohm whne measured ina cell of cell constant 250 ohm whne measured in acell of cell constant 1.15 cm−1 The equivalent conductance (inohm−1cm2equivalent−1) of 0.1 N acetic acid is
View SolutionThree resistances 5Ω,5Ω and 6Ω are connected as shown in figure. If the point S divides the resistance 6Ω into two equal halves, the resistance between points P and S is
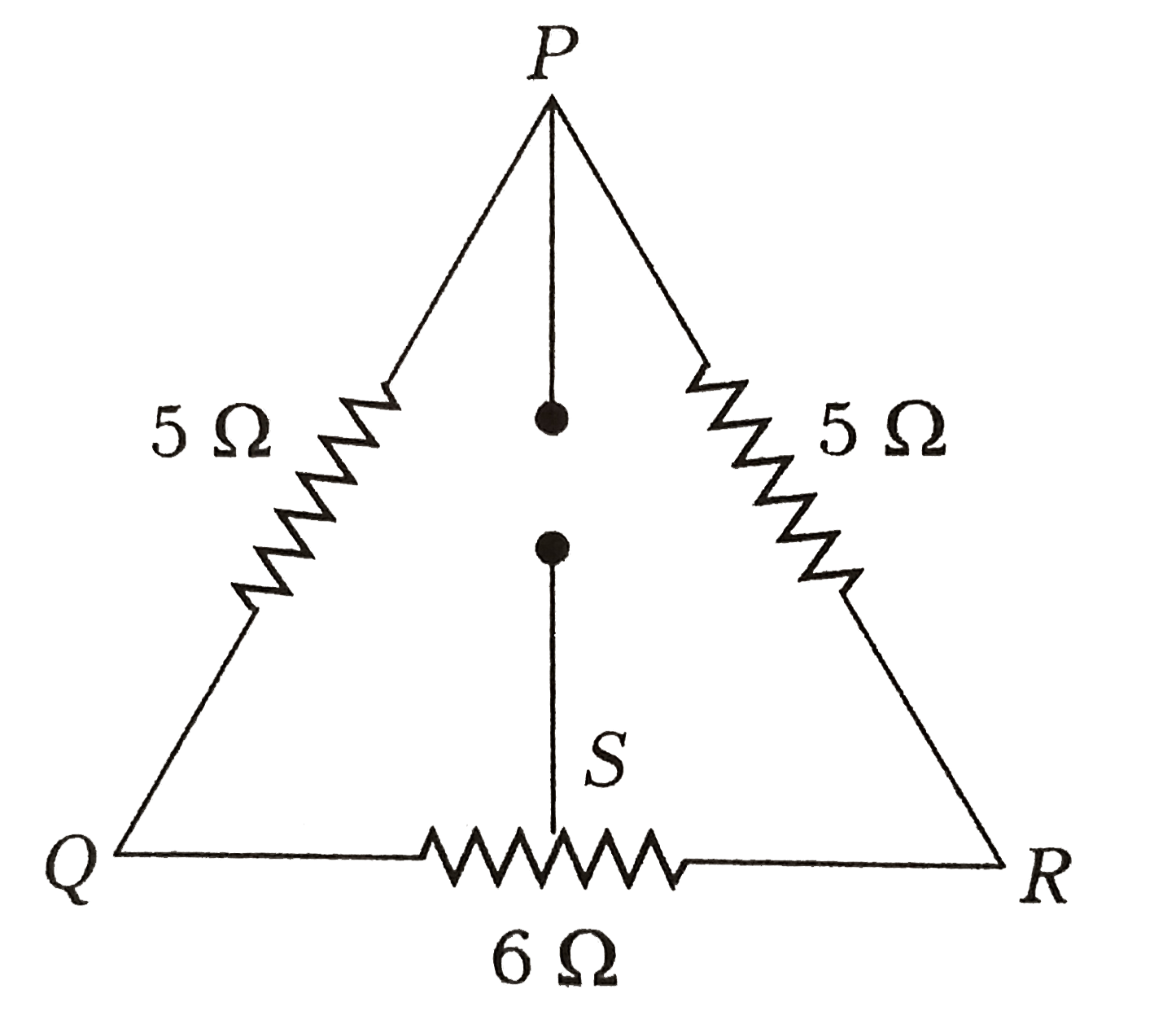
View SolutionThree resistors of 2Ω,3Ω and 4Ω are connected in
parallel. Draw the arrangement and find the equivalent resistance in each case.
View Solution
