What resistance must be connected to a 15 Ω resistance to provide an effective resistance of 6Ω ?
To find the resistance that must be connected to a 15 Ω resistor to provide an effective resistance of 6 Ω, we will follow these steps:
Step 1: Understand the Configuration
Since the effective resistance (6 Ω) is less than one of the resistances (15 Ω), we can conclude that the two resistances are connected in parallel.
Step 2: Write Down the Formula for Parallel Resistance
The formula for the effective resistance (R_P) of two resistors R_1 and R_2 in parallel is given by:
1RP=1R1+1R2
or alternatively,
RP=R1⋅R2R1+R2
Step 3: Substitute Known Values
Let R_1 = 15 Ω (the known resistance) and R_P = 6 Ω (the effective resistance). We need to find R_2 (the unknown resistance). Substituting the known values into the formula gives:
6=15⋅R215+R2
Step 4: Cross-Multiply to Eliminate the Fraction
Cross-multiplying gives:
6(15+R2)=15⋅R2
Step 5: Distribute and Rearrange the Equation
Distributing the 6 on the left side results in:
90+6R2=15R2
Now, rearranging the equation to isolate R_2:
90=15R2−6R2
90=9R2
Step 6: Solve for R_2
Now, divide both sides by 9 to find R_2:
R2=909=10Ω
Conclusion
The resistance that must be connected to the 15 Ω resistor to achieve an effective resistance of 6 Ω is 10 Ω.
---
Since the effective resistance (6 Ω) is less than one of the resistances (15 Ω), we can conclude that the two resistances are connected in parallel.
The formula for the effective resistance (R_P) of two resistors R_1 and R_2 in parallel is given by:
1RP=1R1+1R2
or alternatively,
RP=R1⋅R2R1+R2
Let R_1 = 15 Ω (the known resistance) and R_P = 6 Ω (the effective resistance). We need to find R_2 (the unknown resistance). Substituting the known values into the formula gives:
6=15⋅R215+R2
Cross-multiplying gives:
6(15+R2)=15⋅R2
Distributing the 6 on the left side results in:
90+6R2=15R2
Now, rearranging the equation to isolate R_2:
90=15R2−6R2
90=9R2
Now, divide both sides by 9 to find R_2:
R2=909=10Ω
The resistance that must be connected to the 15 Ω resistor to achieve an effective resistance of 6 Ω is 10 Ω.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(A)43videos
CURRENT ELECTRICITY
- BOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(A) ( MULTIPLE CHOICE TYPE)2videos
CURRENT ELECTRICITY
- BOOK - ICSECHAPTER - CALORIMETRYEXERCISE - EXERCISE-11(B) (NUMERICALS)15videos
CALORIMETRY
- BOOK - ICSECHAPTER - ELECTRO-MAGNETISM EXERCISE - EXERCISE-10 (C) NUMERICALS1videos
ELECTRO-MAGNETISM
Similar Questions
Three resistance of values 2Ω,3Ω and 6Ω are to be connected to produce an effective resistance of 4Ω. This can be done by connecting.
View SolutionA set of n identical resistors, each of resistance RΩ, when connected in series have an effective resistance XΩ and when the resistors are connected in parallel, their effective resistance is YΩ. Find the relation between R, X and Y.
View SolutionA 5 V battery with internal resistance 1Ω and a 2 V battery with internal resistance 0.5Ω are connected to a 3Ω resistor as shown in the figure.The current in the 3Ω resistor is
View SolutionA Wheatstone network consists of four resistances (in cyclic order) 10Ω,5Ω,6Ω,6Ω . The resistance that must be connected across the 10Ωresistance so that the network becomes balanced is (in Ohm):
View SolutionA cell supplies a current of 2 A when it is connected to a 5Ω resistance and supplies a current of 1.2 A, if it is connected to a resistance of 9 Ω. Find the e.m.f and internal resistance of the cell.
View SolutionTwo resistances are joined in parallel whose resultant is 6/8ohm. One of the resistance wire is broken and the effective resistance becomes 2Ω . Then the resistance in ohm of the wire that got broken was
View SolutionThe equivalent resistance of two resistor connected in series is 6Ω and their equivalent resistance is 43Ω. What are the values of resistances ?
View SolutionA cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig.
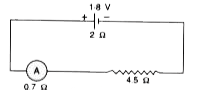
What would be the reading of the ammeter ?View SolutionIn a given network, each resistance has value of 6Ω . The point X is connected to point A by a copper wire of negligible resistance and point Y is connected to point B by the same wire. The effective resistance between X and Y will be
 View Solution
View Solution(a) Given n resistors each of resistance R. How will you combine them to get the (i) maximum (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
(b) Given the resistances of 1Ω,2Ω,3Ω, how will you combine them to get an equivalent resistance of (i) (11/3)Ω (ii) (11/5)Ω (iii) 6Ω (iv) (6/11)Ω ?
(c) Determine the equivalent resistance of networks shown in Figure.
 View Solution
View Solution


