To the potentiometer wire of L and 10Ω resistance, a battery of emf 2.5 volts and a resistance R are connected in series. If a potential difference of 1 volt is balanced across L/2 length, the value of R is Ω will be
30m/s
20m/s
10m/s
5m/s
The correct Answer is:C
To solve the problem, we need to analyze the given information and apply the principles of a potentiometer circuit.
Step 1: Understand the Circuit
We have a potentiometer wire of length L and a resistance of 10Ω. A battery with an emf of 2.5V is connected in series with a resistance R.
Step 2: Determine the Total Resistance
The total resistance in the circuit is the sum of the resistance of the potentiometer wire (which we can consider negligible for the purpose of this calculation) and the fixed resistor:
Rtotal=R+10Ω
Step 3: Calculate the Current in the Circuit
Using Ohm's Law, the current I flowing through the circuit can be calculated using the formula:
I=VRtotal
Substituting the values, we have:
I=2.5VR+10
Step 4: Analyze the Potentiometer Wire
The potential difference (voltage) across a length L/2 of the potentiometer wire is balanced at 1V. The potential difference across the entire length L can be expressed as:
VL=I⋅L
Since VL is the total voltage across the potentiometer wire, we can express the voltage across L/2 as:
VL/2=I⋅L2
Setting VL/2=1V:
1=I⋅L2
Step 5: Substitute the Expression for Current
Substituting the expression for I from Step 3 into the equation from Step 4:
1=(2.5R+10)⋅L2
Step 6: Rearranging the Equation
Rearranging the equation to solve for R:
1=2.5L2(R+10)
2(R+10)=2.5L
R+10=1.25L
R=1.25L−10
Step 7: Conclusion
The value of R can be expressed in terms of L:
R=1.25L−10Ω
We have a potentiometer wire of length L and a resistance of 10Ω. A battery with an emf of 2.5V is connected in series with a resistance R.
The total resistance in the circuit is the sum of the resistance of the potentiometer wire (which we can consider negligible for the purpose of this calculation) and the fixed resistor:
Rtotal=R+10Ω
Using Ohm's Law, the current I flowing through the circuit can be calculated using the formula:
I=VRtotal
Substituting the values, we have:
I=2.5VR+10
The potential difference (voltage) across a length L/2 of the potentiometer wire is balanced at 1V. The potential difference across the entire length L can be expressed as:
VL=I⋅L
Since VL is the total voltage across the potentiometer wire, we can express the voltage across L/2 as:
VL/2=I⋅L2
Setting VL/2=1V:
1=I⋅L2
Substituting the expression for I from Step 3 into the equation from Step 4:
1=(2.5R+10)⋅L2
Rearranging the equation to solve for R:
1=2.5L2(R+10)
2(R+10)=2.5L
R+10=1.25L
R=1.25L−10
The value of R can be expressed in terms of L:
R=1.25L−10Ω
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II66videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-V A20videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)6videos
CIRCULAR MOTION
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective14videos
GEOMETRICAL OPTICS
Similar Questions
A potentiometer wire of length 10 m and resistance 10Ω per meter is connected in serice with a resistance box and a 2 volt battery. If a potential difference of 100 mV is balanced across the whole length of potentiometer wire, then then the resistance introduce introduced in the resistance box will be
View SolutionThe potentiometer wire 10m long and 20 ogm resistance is connected to a 3 volt emf battery and a 10ohm resistance. The value of potential gradient in volt/m of the wire will be
View SolutionTwo batteries one of the emf 3V, internal resistance 1Ω and the other of emf 15V, internal resistance 2Ω are connected in series with a resistance R as shown. If the potential difference between points a and b is zero, the resistance R in Ω is
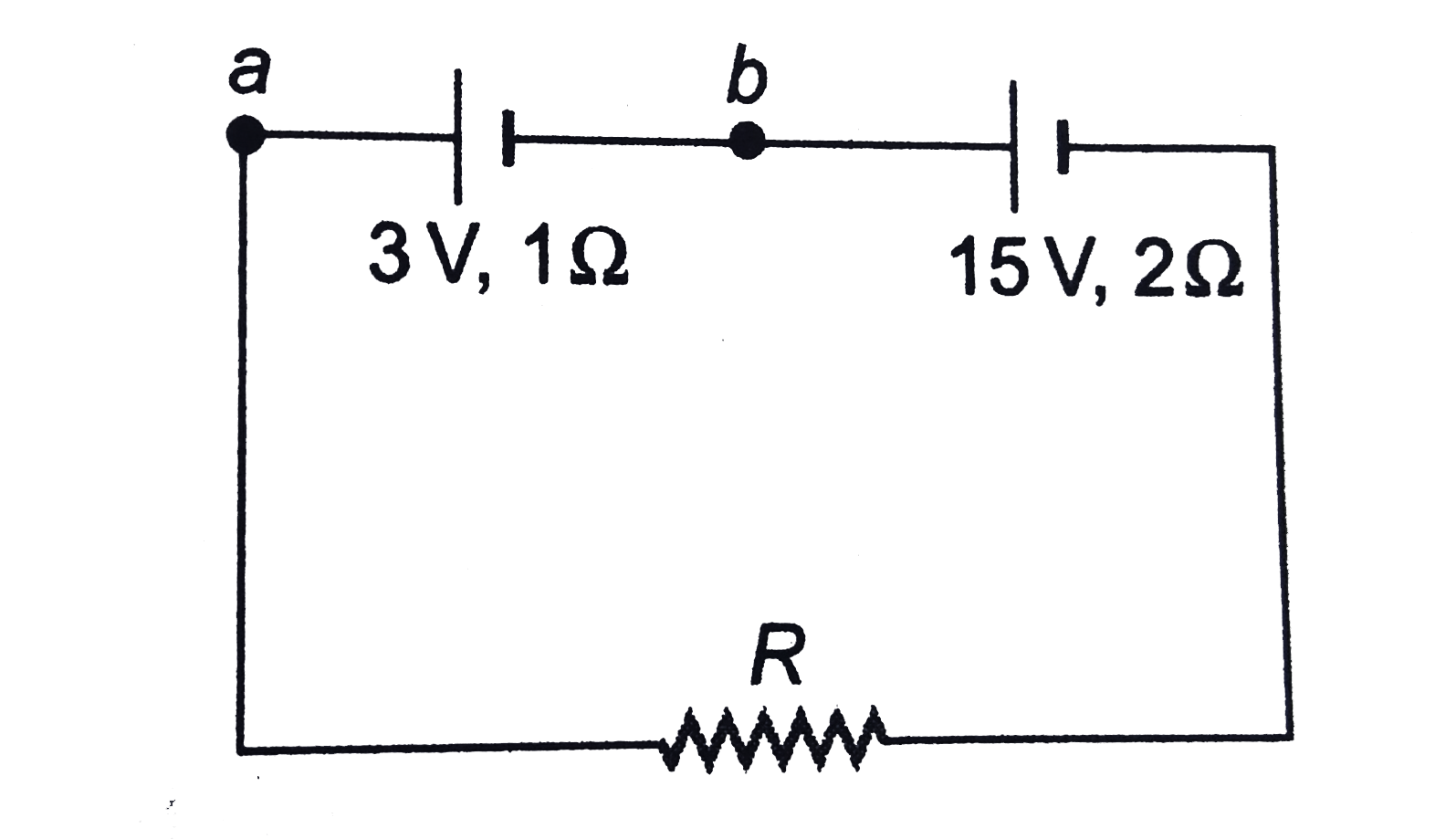 View Solution
View SolutionThe wire of potentiometer has resistance 4Ω and length 1m. It is connected to a cell of emf 2 volt and internal resistance 1Ω. If a cell of emf 1.2 volt is balanced by it, the balancing length will be
View SolutionA potentiometer wire of Length L and a resistance r are connected in series with a battery of e.m.f. E0 and a resistance r1. An unknown e.m.f. E is balanced at a length l of the potentiometer wire. The e.m.f. E will be given by :
View SolutionIf potentiometer wire of length L and resistance 10Ω is connected in series with battery of emf 2.5V and a resistance in its primary circuit.The null point corresponding to a cell of a emf 1V is obtained at a distance L2.If the resistance in the primary circuit is doubled then the position of new null point will be
View SolutionA potentiometer wire is 10 m long and has a resistance of 18Ω. It is connected to a battery of emf 5 V and internal resistance 2Ω. Calculate the potential gradient along the wire.
View SolutionPotentiometer wire length is 10m, having a total resistance of 10Ω, if a battery of emf 2 volt negligible internal resistance and a rheostat is connected to it then potential gradient is 20mV/m find the resistance applied through rheostat:-
View SolutionA potentiometer wire of length 100 cm has a resistance of 10Ω. It is connected in series with a resistance R and cell of emf 2V and negligible resistance. A source of emf 10 mV is balanced against a length of 40cm of the potentiometer wire. What is the value of R?
View SolutionA potentiometer wire has resistance 40Ω and its length is 10m. It is connected by a resistance of 760Ω in series if emf of battery is 2V then potential gradient is:-
View Solution

