One junction of a certain thermoelectric couple is at a fixed temperature r T and the other junction is at temperature T . The thermo electromotive force for this is expressed by E=K(T−Tr)[T0−12(T+Tr)]. At temperature T=12T0, the thermoelectric power is
12KT0
KT0
12KT20
12K(T0−Tr)2
To solve the problem, we need to find the thermoelectric power S at the temperature T=12T0. The thermoelectric power is given by the derivative of the electromotive force E with respect to temperature T.
1. Given Formula:
The electromotive force E is given by:
E=K(T−Tr)(T0−12(T+Tr))
2. Find the Thermoelectric Power:
The thermoelectric power S is defined as:
S=dEdT
We need to differentiate the expression for E with respect to T.
3. Simplify the Expression:
First, we will expand the expression for E:
E=K(T−Tr)(T0−12T−12Tr)
Distributing K(T−Tr):
E=K(T−Tr)(T0−12T−12Tr)=K(T0(T−Tr)−12T(T−Tr)−12Tr(T−Tr))
4. Differentiate E:
Now, we differentiate E with respect to T:
S=dEdT=K(ddT(T0(T−Tr))−12ddT(T(T−Tr))−12TrddT(T−Tr))
The first term gives KT0, the second term gives K(−12(2T−Tr)), and the third term gives 0 since Tr is constant.
5. Combine the Results:
Combining the results:
S=KT0−K(T−12Tr)
6. Substituting T=12T0:
Now we substitute T=12T0:
S=KT0−K(12T0−12Tr)
Simplifying this:
S=KT0−K(12T0−12Tr)=KT0−12KT0+12KTr
This simplifies to:
S=12KT0+12KTr
7. Final Expression:
Thus, the thermoelectric power at T=12T0 is:
S=12KT0
The electromotive force E is given by:
E=K(T−Tr)(T0−12(T+Tr))
The thermoelectric power S is defined as:
S=dEdT
We need to differentiate the expression for E with respect to T.
First, we will expand the expression for E:
E=K(T−Tr)(T0−12T−12Tr)
Distributing K(T−Tr):
E=K(T−Tr)(T0−12T−12Tr)=K(T0(T−Tr)−12T(T−Tr)−12Tr(T−Tr))
Now, we differentiate E with respect to T:
S=dEdT=K(ddT(T0(T−Tr))−12ddT(T(T−Tr))−12TrddT(T−Tr))
The first term gives KT0, the second term gives K(−12(2T−Tr)), and the third term gives 0 since Tr is constant.
Combining the results:
S=KT0−K(T−12Tr)
Now we substitute T=12T0:
S=KT0−K(12T0−12Tr)
Simplifying this:
S=KT0−K(12T0−12Tr)=KT0−12KT0+12KTr
This simplifies to:
S=12KT0+12KTr
Thus, the thermoelectric power at T=12T0 is:
S=12KT0
Similar Questions
If K1 is the equilibrium constant at temperature T1andK2 is the equilibrium constant at temperature T2and If T2>T1 and reaction is endothermic then
View SolutionThe thermo emf E of a thermocouple is found to vary wit temperature T of the junction (cold junction is 0∘C) as
E=40T−T220
The temperature of inversion for the thermocouple isView SolutionIf the cold junction of thermocouple is kept at 0∘C and the hot junction is kept at T∘C, then the relation between neutral temperature (Tn) and temperature of inversion (Ti) is
View SolutionInternal energy of n moles of helium at temperature T1K is equal to the internal energy of 2n moles of oxygen gas at temperature T2K then the value of T1T2will be
View SolutionA solid at temperature T1 is kept in an evacuated chamber at temperature T2>T1 . The rate of increase of temperature of the body is propertional to
View SolutionThe temperature of the cold junction of thermo-couple is 0∘C and the temperature of hot junction is T∘C . The e.m.f . is E=16T−0.04T2μ volts. The temperature of inversion is
View SolutionOne end of a rod of length L and crosssectional area A is kept in a furnace at temperature T1. The other end of the rod is kept at a temperature T2. The thermal conductivity of the matrieal of the rod is K and emissivity of the rod is e. It is gives that T!=Ts+ΔT, where ΔT<<Ts,Ts is the temperature of the surroundings. If ΔT∝(T1−T2) find the proportional constant, consider that heat is lost only by rediation at the end where the temperature of the rod is T1.
 View Solution
View SolutionThe stress-strain graph for a metallic wire is shown at two different temperature, T1 and T2 which temperature is high T1 or T2 ?
View SolutionThe cold junction of a thermocouple is at 0∘C. The thermo e.m.f. ε, in volts, generated in this thermocouple varies with temperature t∘C of the hot junction as ε=6+4t−t232. The neutral temperature of the thermocouple
View SolutionThe resistance R of a conductor varies with temperature t as shown in the figure. If the variation is represented by Rt=R0[1+αt+βt2], then
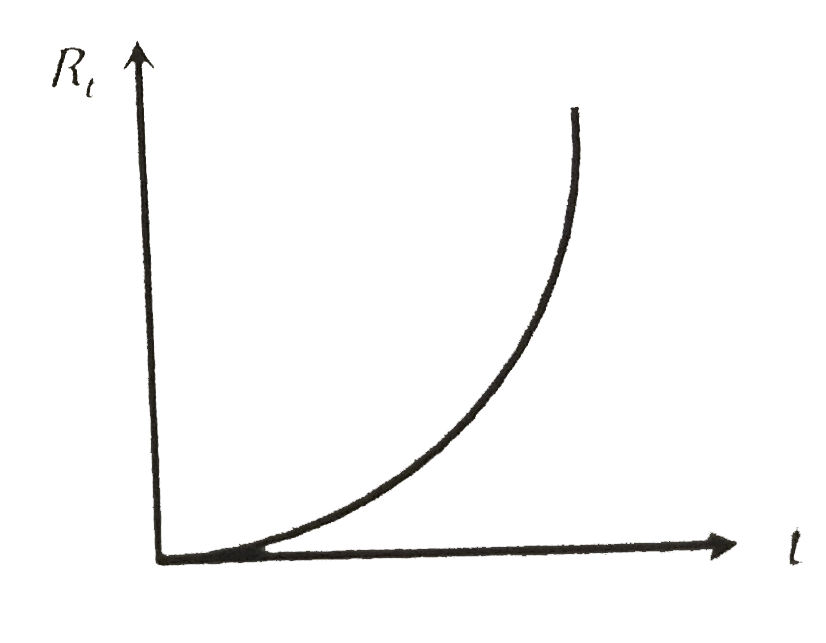 View Solution
View Solution

