Question

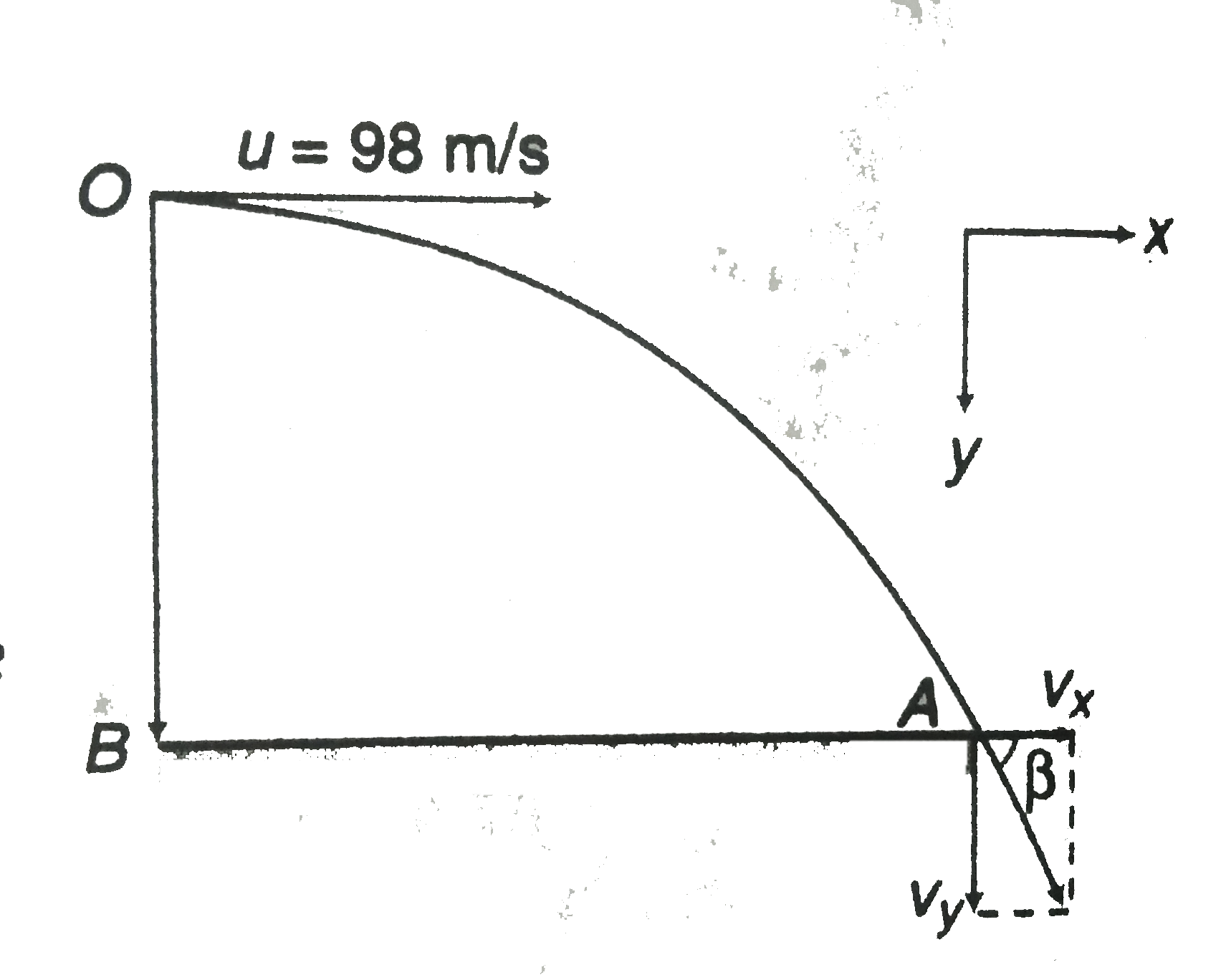
A projectile is fired horizontally with a velocity of $98m{s}^{-1}$ from the top of a hill 490 m high. Find (i) the time taken to reach the ground (ii) the distance of the target from the hill and (iii) the velocity with which the projectile hits the ground.

Answer

(i) 10 sec, (ii) 980 m, (iii) `98sqrt(2) m//sec`

Explanation

To solve the problem step-by-step, we will break it down into three parts: (i) finding the time taken to reach the ground, (ii) calculating the distance of the target from the hill, and (iii) determining the velocity with which the projectile hits the ground.

Step 1: Time Taken to Reach the Ground

1. Identify the known values:
- Height of the hill (s) = 490 m
- Initial vertical velocity (u) = 0 m/s (since it is fired horizontally)
- Acceleration due to gravity (a) = g = 9.8 m/s²

2. Use the equation of motion:
The equation we will use is:
\( s = ut + \frac{1}{2} a t^2 \)
Substituting the known values:
\( 490 = 0 \cdot t + \frac{1}{2} \cdot 9.8 \cdot t^2 \)
This simplifies to:
\( 490 = 4.9 t^2 \)

3. Solve for t:
Rearranging gives:
\( t^2 = \frac{490}{4.9} = 100 \)
Taking the square root:
\( t = 10 \text{ seconds} \)

Step 2: Distance of the Target from the Hill

1. Identify the horizontal velocity:
The horizontal velocity (Vx) is given as 98 m/s.

2. Calculate the horizontal distance (d):
The horizontal distance traveled while the projectile is in the air can be calculated using:
\( d = Vx \cdot t \)
Substituting the values:
\( d = 98 \cdot 10 = 980 \text{ meters} \)

Step 3: Velocity with which the Projectile Hits the Ground

1. Calculate the vertical component of the velocity (Vy) just before hitting the ground:
Using the energy conservation principle or the kinematic equation:
\( v_y^2 = u_y^2 + 2as \)
Here, \(u_y = 0\):
\( v_y^2 = 0 + 2 \cdot 9.8 \cdot 490 \)
\( v_y^2 = 9604 \implies v_y = \sqrt{9604} = 98 \text{ m/s} \)

2. Calculate the resultant velocity (V):
The resultant velocity when the projectile hits the ground can be found using:
\( V = \sqrt{V_x^2 + V_y^2} \)
Substituting the values:
\( V = \sqrt{98^2 + 98^2} = \sqrt{2 \cdot 98^2} = 98\sqrt{2} \approx 138.59 \text{ m/s} \)

Summary of Results
- (i) Time taken to reach the ground: 10 seconds
- (ii) Distance of the target from the hill: 980 meters
- (iii) Velocity with which the projectile hits the ground: 98√2 m/s or approximately 138.59 m/s