A stone is projected from point P on the inclined plane with velocity v0=10m/sec directed perpendicular to the plane. The time taken (in second) by the stone to strike the horizontal ground S is (Given PO=l=10meter)(Take g=10m/s2)

1.5 sce
1.4 sec
2 sec
2.3 sec
The correct Answer is:C
Step by step video & image solution for A stone is projected from point P on the inclined plane with velocity v_(0) = 10 m//sec directed perpendicular to the plane. The time taken (in second) by the stone to strike the horizontal ground S is (Given PO = l = 10meter)(Take g = 10m//s^(2)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time
View SolutionA ball is projected from point A with velocity 10ms−1 perpendicular to the inclined plane as shown in figure. Range of the ball on the inclined plane is

View SolutionA ball is projected from a point in a horizontal plane with a velocity of 20 m/s at 30∘ with the horizontal. Coefficient of restitution is 0.8, then
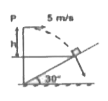
View SolutionA particle of mass m is thrown horizontally from point P , as shown in the figure, with speed 5m/s. It strikes an inclined plane perpendicularly as shown. The inclination of the plane is 30∘ with the horizontal. Then, the height h shown in the figure is ( Take g=10m/s2 ) .
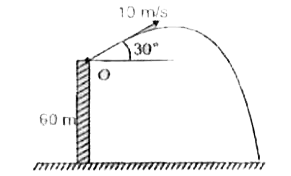
View SolutionA ball is projected from a point O as shown in figure it will strike the ground after (g = 10 m/s2 )
View SolutionA stone is projected from the ground with velocity 50ms at an angle of 30∘. It crosses a wall after 3 sec. How far beyond the wall the stone will strike the ground (g=10msec2?
View SolutionA stone is projected from the ground with velocity 50ms at an angle of 30∘. It crosses a wall after 3 sec. How far beyond the wall the stone will strike the ground (g=10msec2?
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘ with velocity of 40m/s at an angle of 60∘ with horizontal. Find the speed of the particle when its velocity vector is parallel to the plane. Take g=10m/s2.
View SolutionA person, standing on the roof of a 40 m high tower, throws a ball vertically upwards with speed 10 m/s. Two seconds later, he throws another ball again in vertical direction (use g=10ms2). Both the balls hit the ground simultaneously.
View SolutionA stone is projected from the ground with a velocity of 14ms−1. One second later it clears a wall 2m high. The angle of projection is (g=10ms−2)
View Solution
