A block is thrown with a velocity of 2m/s−1 (relative to ground) on a belt, which is moving with velocity 4ms−1 in opposite direction of the initial velocity of block. If the block stops slipping on the belt after 4sec of the throwing then choose the correct statements (s)
Displacement with respect to ground is zero after 2.66 s and magnitude of displacement with respect to ground is 12 m after 4s.
Magnitude of displacement with respect to ground in 4s is 4 m.
Magnitude of displacement with respect to belt in 4s is 12 m.
Displacement with respect to ground is zero in 8/3 s.
The correct Answer is:B, C, D
To solve the problem step by step, we will analyze the motion of the block and the belt separately and then combine the results to determine the correct statements.
Step 1: Understand the Initial Conditions
- The block is thrown with a velocity of vb=2m/s (relative to the ground).
- The belt is moving with a velocity of vbelt=4m/s in the opposite direction to the block's initial velocity.
Step 2: Determine the Initial Relative Velocity
Since the block is thrown in the opposite direction to the belt's motion, the initial velocity of the block relative to the belt can be calculated as:
vrelative=vb−vbelt=2m/s−(−4m/s)=2+4=6m/s
Step 3: Calculate the Acceleration of the Block
The block stops slipping after t=4s. We can use the formula for final velocity:
v=u+at
Where:
- v=0 (the block stops slipping),
- u=6m/s (initial relative velocity),
- t=4s.
Rearranging gives:
0=6+a(4)
Solving for a:
a=−64=−1.5m/s2
Step 4: Calculate the Displacement of the Block
Using the equation of motion:
x=ut+12at2
Substituting the values:
x=6×4+12×(−1.5)×(42)
Calculating:
x=24−12×1.5×16=24−12=12m
Step 5: Calculate the Displacement of the Belt
The displacement of the belt during the same time can be calculated as:
xbelt=vbelt×t
Substituting the values:
xbelt=4×4=16m
Step 6: Analyze the Results
- The block moves 12m relative to the ground.
- The belt moves 16m relative to the ground.
Conclusion
The block stops slipping after 4s and the distances covered are:
- Block: 12m
- Belt: 16m
Now, we can choose the correct statements based on these calculations.
- The block is thrown with a velocity of vb=2m/s (relative to the ground).
- The belt is moving with a velocity of vbelt=4m/s in the opposite direction to the block's initial velocity.
Since the block is thrown in the opposite direction to the belt's motion, the initial velocity of the block relative to the belt can be calculated as:
vrelative=vb−vbelt=2m/s−(−4m/s)=2+4=6m/s
The block stops slipping after t=4s. We can use the formula for final velocity:
v=u+at
Where:
- v=0 (the block stops slipping),
- u=6m/s (initial relative velocity),
- t=4s.
0=6+a(4)
Solving for a:
a=−64=−1.5m/s2
Using the equation of motion:
x=ut+12at2
Substituting the values:
x=6×4+12×(−1.5)×(42)
Calculating:
x=24−12×1.5×16=24−12=12m
The displacement of the belt during the same time can be calculated as:
xbelt=vbelt×t
Substituting the values:
xbelt=4×4=16m
- The block moves 12m relative to the ground.
- The belt moves 16m relative to the ground.
The block stops slipping after 4s and the distances covered are:
- Block: 12m
- Belt: 16m
Topper's Solved these Questions
Similar Questions
A body of mass 2kg moving with a velocity 3m/s collides with a body of mass 1kg moving with a velocity of 4m/s in opposite direction. If the collision is head on and completely inelastic, then
View SolutionA car A moves with velocity 15ms−1 and B with velocity 20ms−1 are moving in opposite directions as shown in . Find the relative velocity of B w.r.t. A and w.r.t. B.
 .
.
View SolutionA body has an initial velocity of 3ms−1 and has an acceleration of 1ms−2 normal to the direction of the initial velocity. Then its velocity 4s after the start is.
View SolutionA motor is fixed inside a box which is moving upwards with velocity 5m/s. String is winding at the rate 3m/s Then the velocity of block A will be.
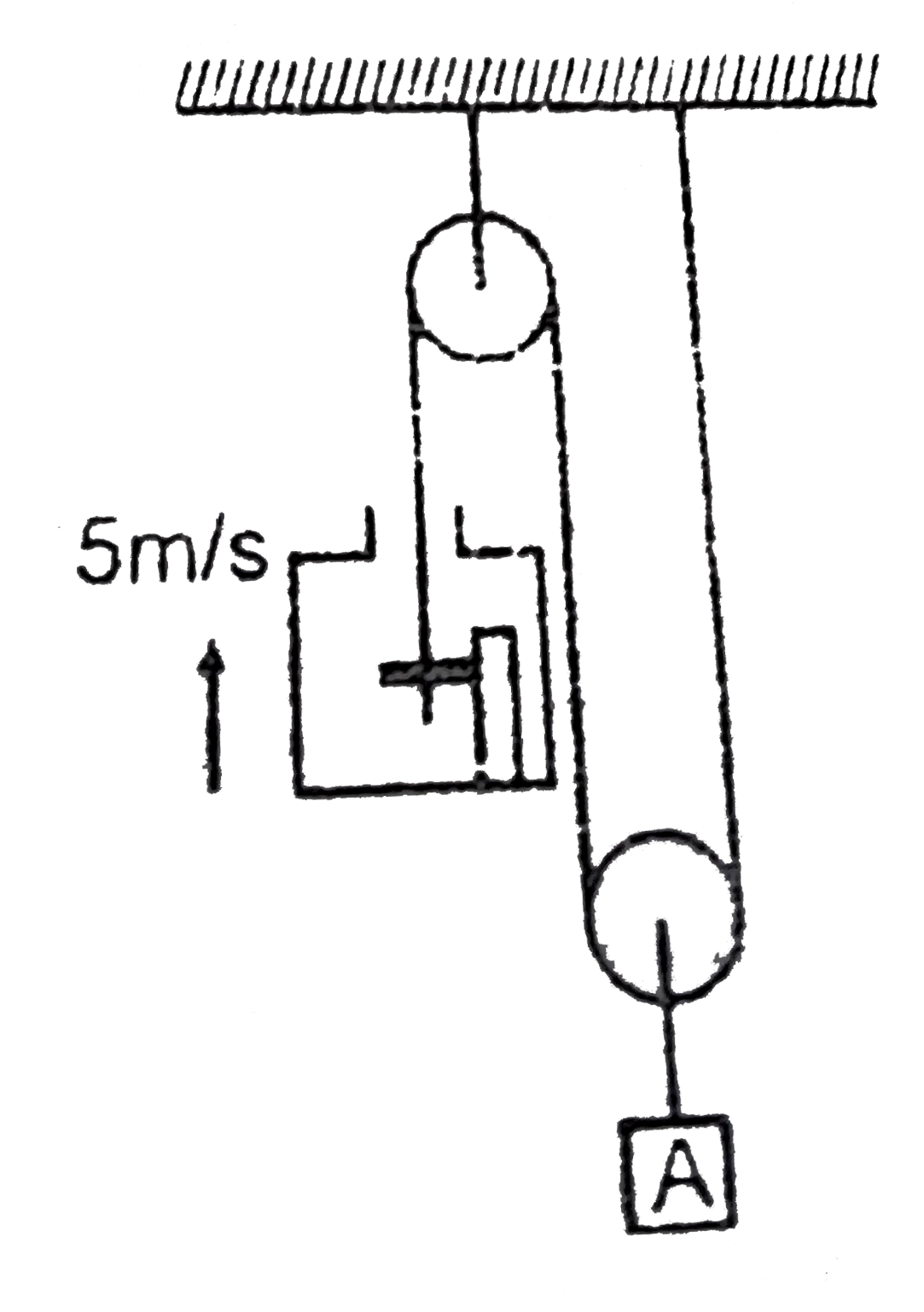
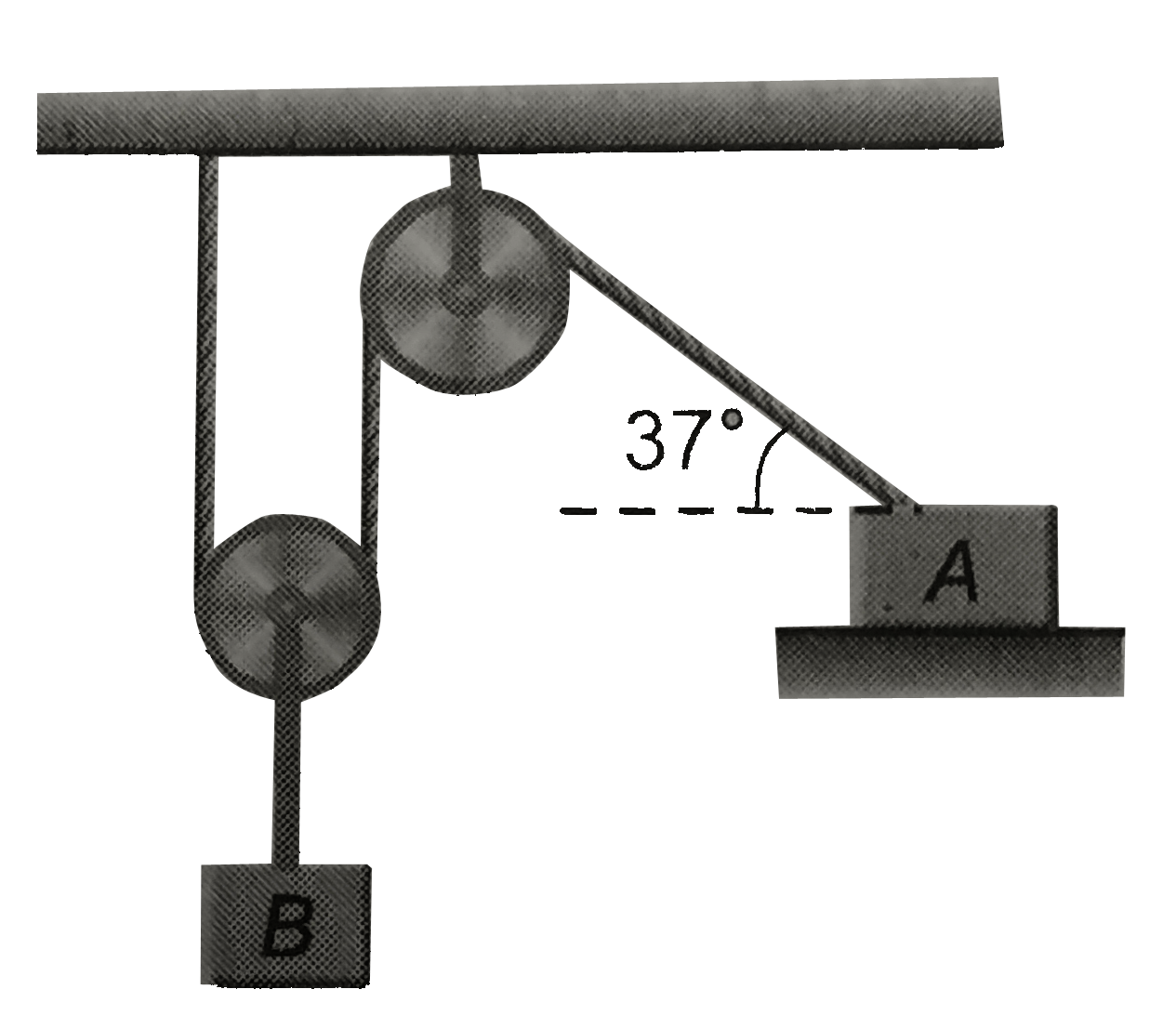
View SolutionIn the figure shown the block B moves with , velocity 10ms−1. The velocity of A in the position shown is
View SolutionIn the system shown, the block A is moving down eith velocity v1 and C is moving up with velocity v3. Express velocity of the block B in terms of velocities of the blocks a and C.

View SolutionA body of mass 3kg moving with a velocity of 4m/s towards left collides head on with a body of mass 4kg moving in opposite direction with a velocity of 3m/s. After collision the two bodies stick together and move with a common velocity which is
View SolutionA 100 kg block is started with a speed of 2.0ms−1 on a long, rough belt kept fixed in a horizontal position. The coefficient of kinetic friction between the block and the belt is 0.20. (a) calculate the change in the internal energy of the block-belt system as the block comes to a stop on the belt. (b) consider the situation from a frame of reference moving at 2.0ms−1 along the initial velocity of the block. as seen from this frame, the block is gently put on a moving belt and in due time the block starts moving with the belt at 2.0ms−1, calculate the increase in the kinetic energy of the block as it stops slipping past the belt. (c ) find the work done in this frame by the external force holding the belt.
View SolutionA block of mass 5 kg moves from left to right with a velocity of 2ms−1 and collides with another block of mass 3 kg moving along the same line in the opposite direction with velocity 4ms−1.
(i) If the collision is perfectly elastic, determine velocities of both the blocks after their collision.
(ii) If coefficient of restitution is 0.6, determine velocities of both the blocks after their collision.
View SolutionThe velocity acquired by a body moving with uniformaccelertion is 30ms−1 in 2s and 60ms−1 in 4s, The initial velocity is .
View Solution