A man on a rectilinearly moving cart, facing the direction of motion, throws a ball straight up with respect to himself
The ball will always return to him.
The ball will never return to him.
The ball will return to him if the cart moves with constant velocity
The ball will fall behind him if the cart moves with some positive acceleration.
The correct Answer is:C, D
To solve the problem, we need to analyze the motion of the ball thrown by the man on the moving cart. The key points to consider are the relative motion of the ball and the cart, as well as the effects of acceleration.
1. Identify the Initial Conditions:
- The cart is moving with a constant velocity vc in a straight line.
- The man throws the ball vertically upward with respect to himself. This means that the initial horizontal velocity of the ball vx is equal to the velocity of the cart, vc.
2. Analyze the Motion of the Ball:
- When the ball is thrown straight up, it has an initial vertical velocity vy (upward).
- The horizontal component of the ball's velocity remains vc throughout its flight because there are no horizontal forces acting on it (assuming air resistance is negligible).
3. Determine the Motion of the Cart:
- The cart continues to move with a constant velocity vc.
- If the cart is moving with constant velocity, it will cover a certain distance while the ball is in the air.
4. Consider the Time of Flight:
- The time the ball spends in the air can be calculated using the vertical motion equations. The ball will rise to a maximum height and then fall back down.
- The total time of flight t can be determined using the formula for vertical motion:
t=2vyg
where g is the acceleration due to gravity.
5. Calculate the Distances:
- During the time t, the cart travels a horizontal distance dcart=vc⋅t.
- The ball also travels horizontally at the same speed vc, so it will also cover the same horizontal distance dball=vc⋅t.
6. Conclusion on the Return of the Ball:
- If the cart is moving with constant velocity, the horizontal distance traveled by the ball and the cart will be the same, meaning the ball will return to the man.
- If the cart accelerates positively, the horizontal distance traveled by the cart will be greater than that of the ball, causing the ball to fall behind the cart.
Final Options Analysis:
- Option A: The ball will always return to him. (Incorrect, as it depends on the cart's motion)
- Option B: The ball will never return to him. (Incorrect, as it can return if the cart moves at constant velocity)
- Option C: The ball will return to him if the cart moves with constant velocity. (Correct)
- Option D: The ball will fall behind him if the cart moves with some positive acceleration. (Correct)
- The cart is moving with a constant velocity vc in a straight line.
- The man throws the ball vertically upward with respect to himself. This means that the initial horizontal velocity of the ball vx is equal to the velocity of the cart, vc.
- When the ball is thrown straight up, it has an initial vertical velocity vy (upward).
- The horizontal component of the ball's velocity remains vc throughout its flight because there are no horizontal forces acting on it (assuming air resistance is negligible).
- The cart continues to move with a constant velocity vc.
- If the cart is moving with constant velocity, it will cover a certain distance while the ball is in the air.
- The time the ball spends in the air can be calculated using the vertical motion equations. The ball will rise to a maximum height and then fall back down.
- The total time of flight t can be determined using the formula for vertical motion:
t=2vyg
where g is the acceleration due to gravity.
- During the time t, the cart travels a horizontal distance dcart=vc⋅t.
- The ball also travels horizontally at the same speed vc, so it will also cover the same horizontal distance dball=vc⋅t.
- If the cart is moving with constant velocity, the horizontal distance traveled by the ball and the cart will be the same, meaning the ball will return to the man.
- If the cart accelerates positively, the horizontal distance traveled by the cart will be greater than that of the ball, causing the ball to fall behind the cart.
- Option A: The ball will always return to him. (Incorrect, as it depends on the cart's motion)
- Option B: The ball will never return to him. (Incorrect, as it can return if the cart moves at constant velocity)
- Option C: The ball will return to him if the cart moves with constant velocity. (Correct)
- Option D: The ball will fall behind him if the cart moves with some positive acceleration. (Correct)
Topper's Solved these Questions
Similar Questions
In the figure the top view of a compartment of a train is shown. A man is sitting at a corner 'B' of the compartment . The man throws a ball ( with respect to himself ) along the surface of the floor towards the corner 'D' of the compartment of the train. The ball hits the corner 'A' of the compartment, then find the time at which it hits A after the ball is thrown . Assume no other collision during motion and floor is smooth. The length of the compartment is given 'l' and the train is moving with constant acceleration 'a' in the direction shown in the figure.
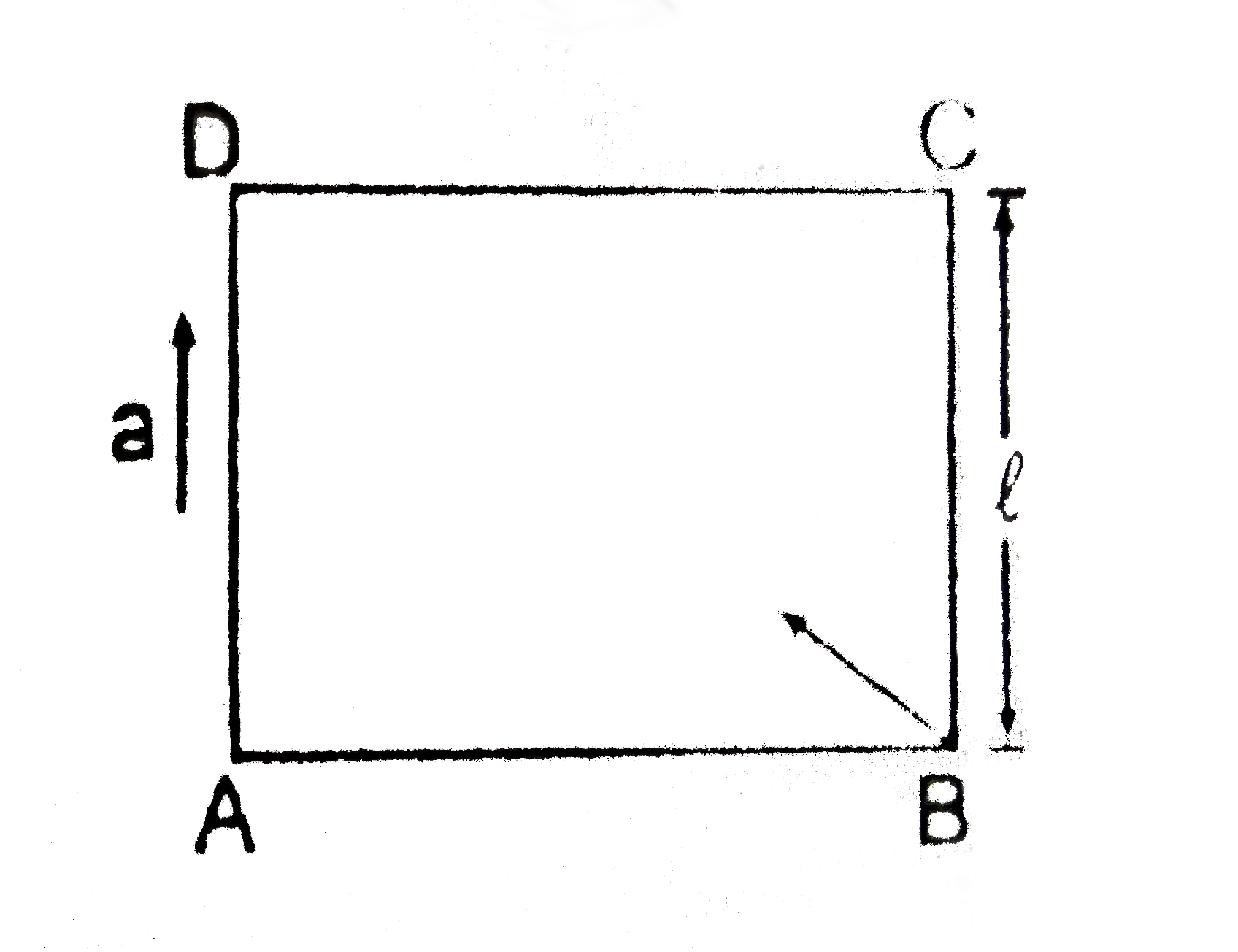
View SolutionIn a gravity free space, man of mass M standing at a height h above the floor, throws a ball of mass m straight down with a speed u. When the ball reaches the floor, the distance of the man above the floor will be.
View SolutionA train is running at a constant speed of 90 km/h on a straight track. A person standing at the top of a boggey moves in the direction of motion of the train such that he covers 1 meters on the train each second. The speed of the person with respect to ground to -
View SolutionA man in an open car moving with high speed, throws a ball his full capacity along the direction of the motion of the car . Now the same man throws the same ball when the car is not moving. In which case the ball possesses more kinetic energy in
(a) ground frame
(b) car frame.
View SolutionA boy is sitting in a car moving with uniform velocity. The boy throws a ball vertically upwards which falls back into his hands. A man standing on the road watches the motion of the ball. The path of the motion of the ball will be:
View SolutionA man in a lift ascending with an upward acceleration a throws a ball vertically upwards with a velocity v with respect to himself and catches it after t1 seconds. After wards when the lift is descending with the same acceleration a acting downwards the man again throws the ball vertically upwards with the same velocity with respect to him and catches it after t2 seconds?
View SolutionA man standing on the edge of a cliff throws a stone straight up with initial speed (u) and then throws another stone straight down with same initial speed and from the same position. Find the ratio of the speeds. The stones would have attained when they hit ground at the base of the cliff.
View SolutionA ball moving along a straight line collides elastically with another stationary ball of the same mass. At the moment of collision, the angle between the straight line passing through the centres of the balls and the direction of tr initial motion of the striking ball is θ, find the fraction of the kinetic energy of the striking ball converted into potential energy at the moment of the maximum deformation.
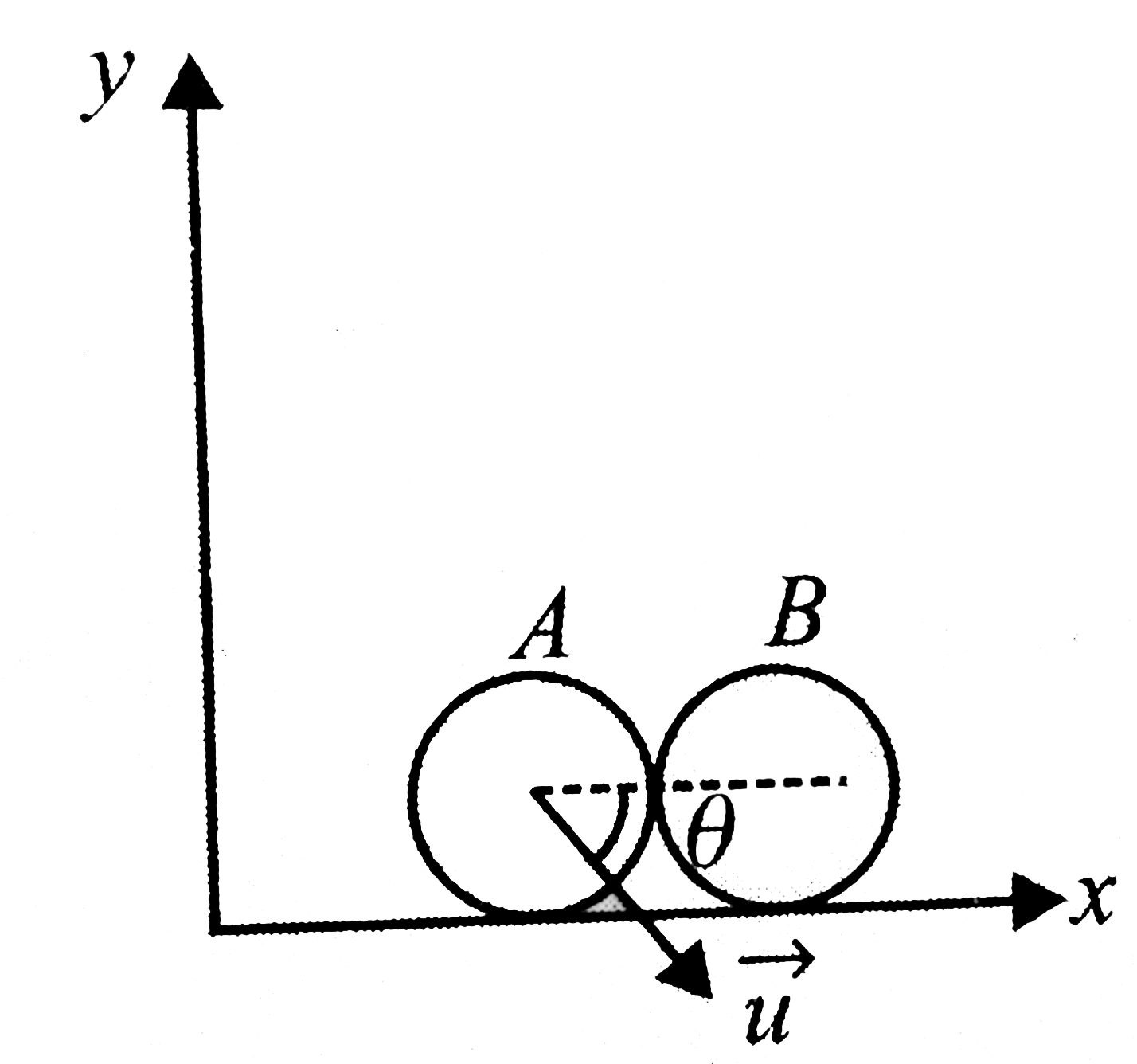
View SolutionA car is travelling at a velocity 10 km h−1 on a straight road. The driver of the car throws a parcel with a velocity 10√2kmh−1 with respect to the car, when the car is passing by a man standing on the side of the road. If the parcel is to reach the man, the direction of throw makes the following angle with the direction of motion of the car
View SolutionA person sitting in an open car moving at constant velocity throws a ball vertically up into air. The ball falls
View Solution
