If A+B+C=π2, then find the value of tanAtanB+tanBtanC+tanCtanA
To solve the problem, we need to find the value of tanAtanB+tanBtanC+tanCtanA given that A+B+C=π2.
1. Use the given equation:
A+B+C=π2
We can rearrange this to express C:
C=π2−(A+B)
2. Apply the tangent function:
We know that:
tan(A+B)=tan(π2−C)
Using the identity tan(π2−x)=cotx, we have:
tan(A+B)=cotC
3. Use the tangent addition formula:
The tangent addition formula states:
tan(A+B)=tanA+tanB1−tanAtanB
Therefore, we can equate:
tanA+tanB1−tanAtanB=cotC
4. Express cotangent in terms of tangent:
Recall that cotC=1tanC. Thus, we can rewrite the equation as:
tanA+tanB1−tanAtanB=1tanC
5. Cross-multiply:
Cross-multiplying gives us:
tanC(tanA+tanB)=1−tanAtanB
6. Rearranging the equation:
Rearranging the equation, we get:
tanAtanB+tanBtanC+tanCtanA=1
7. Conclusion:
Hence, the value of tanAtanB+tanBtanC+tanCtanA is:
1
A+B+C=π2
We can rearrange this to express C:
C=π2−(A+B)
We know that:
tan(A+B)=tan(π2−C)
Using the identity tan(π2−x)=cotx, we have:
tan(A+B)=cotC
The tangent addition formula states:
tan(A+B)=tanA+tanB1−tanAtanB
Therefore, we can equate:
tanA+tanB1−tanAtanB=cotC
Recall that cotC=1tanC. Thus, we can rewrite the equation as:
tanA+tanB1−tanAtanB=1tanC
Cross-multiplying gives us:
tanC(tanA+tanB)=1−tanAtanB
Rearranging the equation, we get:
tanAtanB+tanBtanC+tanCtanA=1
Hence, the value of tanAtanB+tanBtanC+tanCtanA is:
1
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - BASIC MATHS,LOGARITHIM, TRIGNOMETRIC RATIO AND IDENTITIES AND TRIGNOMETRIC EQUATION EXERCISE - DO YOURSELF 113videos
BASIC MATHS,LOGARITHIM, TRIGNOMETRIC RATIO AND IDENTITIES AND TRIGNOMETRIC EQUATION
- BOOK - ALLENCHAPTER - BASIC MATHS,LOGARITHIM, TRIGNOMETRIC RATIO AND IDENTITIES AND TRIGNOMETRIC EQUATION EXERCISE - DO YOURSELF 121videos
BASIC MATHS,LOGARITHIM, TRIGNOMETRIC RATIO AND IDENTITIES AND TRIGNOMETRIC EQUATION
- BOOK - ALLENCHAPTER - BASIC MATHS,LOGARITHIM, TRIGNOMETRIC RATIO AND IDENTITIES AND TRIGNOMETRIC EQUATION EXERCISE - DO YOURSELF 91videos
BASIC MATHS,LOGARITHIM, TRIGNOMETRIC RATIO AND IDENTITIES AND TRIGNOMETRIC EQUATION
- BOOK - ALLENCHAPTER - BASIC MATHS LOGARITHIM TRIGNOMETRIC RATIO AND IDENTITIES AND TRIGNOMETRIC EQUATION EXERCISE - ILLUSTRATIONS39videos
BASIC MATHS LOGARITHIM TRIGNOMETRIC RATIO AND IDENTITIES AND TRIGNOMETRIC EQUATION
- BOOK - ALLENCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - All Questions1videos
INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
If ABC D is a cyclic quadrilateral, then find the value of sinA+sinB−sinC−sinD
If A+B+C=π2, then find the value of tanAtanB+tanBtanC+tanCtanAView SolutionFind the values of A,B and C
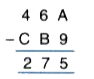 View Solution
View SolutionIf cosA=12andsinB=1√2 , find the value of : tanA−tanB1+tanAtanB : Here angles A and B from different right triangle .
View SolutionIf A+B+C=π, then find the minimum value of cot2A+cot2B+cot2C
View SolutionIn triangle ABC, if ∠A=π4, then find all possible values of tanBtanC.
View SolutionIf sinA=√32andcosB=√32 , find the value of : tanA−tanB1+tanAtanB
View SolutionIf tanA=2,secB=−53, where π<A<3π2, π2<B<π, then
i) Find the value of tan(A+B),
ii) find the quadrant in which (A+B) terminates.View SolutionA triangle ABC is such that sin(2A+B)=12 and If A,B and C are in A.P., then find the value of A and C
View SolutionIf [abc]=2, then find the value of [(a+2b−c)(a−b)(a−b−c)].
View SolutionIf in triangle ABC,δ=a2−(b−c)2 , then find the value of tanA.
View Solution

