If ABCD is a cyclic quadrilateral, then find the value of sinA+sinB−sinC−sinD
To solve the problem, we need to find the value of sinA+sinB−sinC−sinD given that ABCD is a cyclic quadrilateral.
1. Understanding Cyclic Quadrilaterals:
In a cyclic quadrilateral, the sum of the opposite angles is 180∘. Therefore, we have:
A+C=180∘andB+D=180∘
2. Expressing Angles C and D:
From the above relationships, we can express angles C and D in terms of angles A and B:
C=180∘−AandD=180∘−B
3. Substituting in the Expression:
Now, substitute C and D into the expression sinA+sinB−sinC−sinD:
sinA+sinB−sin(180∘−A)−sin(180∘−B)
4. Using the Sine Identity:
We know that sin(180∘−θ)=sinθ. Thus, we can simplify:
sinA+sinB−sinA−sinB
5. Simplifying the Expression:
After substituting, we see that:
sinA+sinB−sinA−sinB=0
6. Final Result:
Therefore, the value of sinA+sinB−sinC−sinD is:
0
In a cyclic quadrilateral, the sum of the opposite angles is 180∘. Therefore, we have:
A+C=180∘andB+D=180∘
From the above relationships, we can express angles C and D in terms of angles A and B:
C=180∘−AandD=180∘−B
Now, substitute C and D into the expression sinA+sinB−sinC−sinD:
sinA+sinB−sin(180∘−A)−sin(180∘−B)
We know that sin(180∘−θ)=sinθ. Thus, we can simplify:
sinA+sinB−sinA−sinB
After substituting, we see that:
sinA+sinB−sinA−sinB=0
Therefore, the value of sinA+sinB−sinC−sinD is:
0
Topper's Solved these Questions
- BASIC MATHS,LOGARITHIM, TRIGNOMETRIC RATIO AND IDENTITIES AND TRIGNOMETRIC EQUATION BOOK - ALLENCHAPTER - BASIC MATHS,LOGARITHIM, TRIGNOMETRIC RATIO AND IDENTITIES AND TRIGNOMETRIC EQUATION EXERCISE - DO YOURSELF 11
3 Videos
- BASIC MATHS,LOGARITHIM, TRIGNOMETRIC RATIO AND IDENTITIES AND TRIGNOMETRIC EQUATION BOOK - ALLENCHAPTER - BASIC MATHS,LOGARITHIM, TRIGNOMETRIC RATIO AND IDENTITIES AND TRIGNOMETRIC EQUATION EXERCISE - DO YOURSELF 12
1 Videos
- BASIC MATHS,LOGARITHIM, TRIGNOMETRIC RATIO AND IDENTITIES AND TRIGNOMETRIC EQUATION BOOK - ALLENCHAPTER - BASIC MATHS,LOGARITHIM, TRIGNOMETRIC RATIO AND IDENTITIES AND TRIGNOMETRIC EQUATION EXERCISE - DO YOURSELF 9
1 Videos
- BASIC MATHS LOGARITHIM TRIGNOMETRIC RATIO AND IDENTITIES AND TRIGNOMETRIC EQUATION BOOK - ALLENCHAPTER - BASIC MATHS LOGARITHIM TRIGNOMETRIC RATIO AND IDENTITIES AND TRIGNOMETRIC EQUATION EXERCISE - ILLUSTRATIONS
39 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ALLENCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - All Questions
1 Videos
Similar Questions
If ABC D is a cyclic quadrilateral, then find the value of sinA+sinB−sinC−sinD
If A+B+C=π2, then find the value of tanAtanB+tanBtanC+tanCtanA
View SolutionIf ABCD is a cyclic quadrilateral, then the value of cosA-cosB+cosC-cosD is equal to
View SolutionIn Figure, ABCD is a cyclic quadrilateral. Find the value of a and b.
View SolutionLet ABCD be a cyclic quadrilateral then
Statement:1 sinA + sinB+ sinC + sinD=0
and Statement:2 cosA + cosB + cosC + cosD=0
View SolutionIn a cyclic quadrilateral ABCD, the value of 2+∑cosAcosB, is
View SolutionIf ABCD is a cyclic quadrilateral, then prove that AC.BD=AB.CD+BC.AD
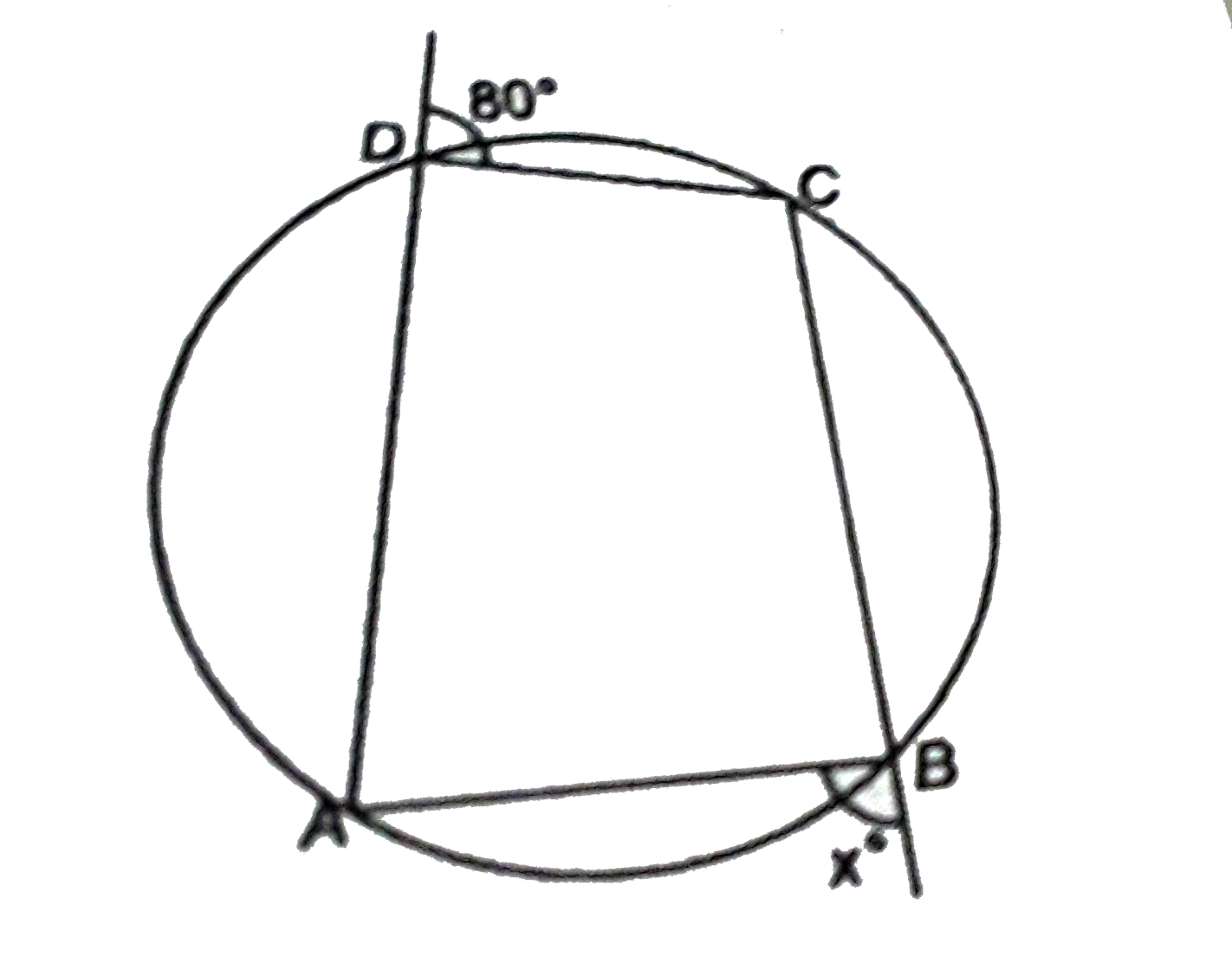
View SolutionIn the adjoining figure, if ABCD is a cyclic quadrilateral, find the value of x.
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.

View SolutionABCD is a cyclic quadrilateral (see Figure). Find the angles of the cyclic quadrilateral.
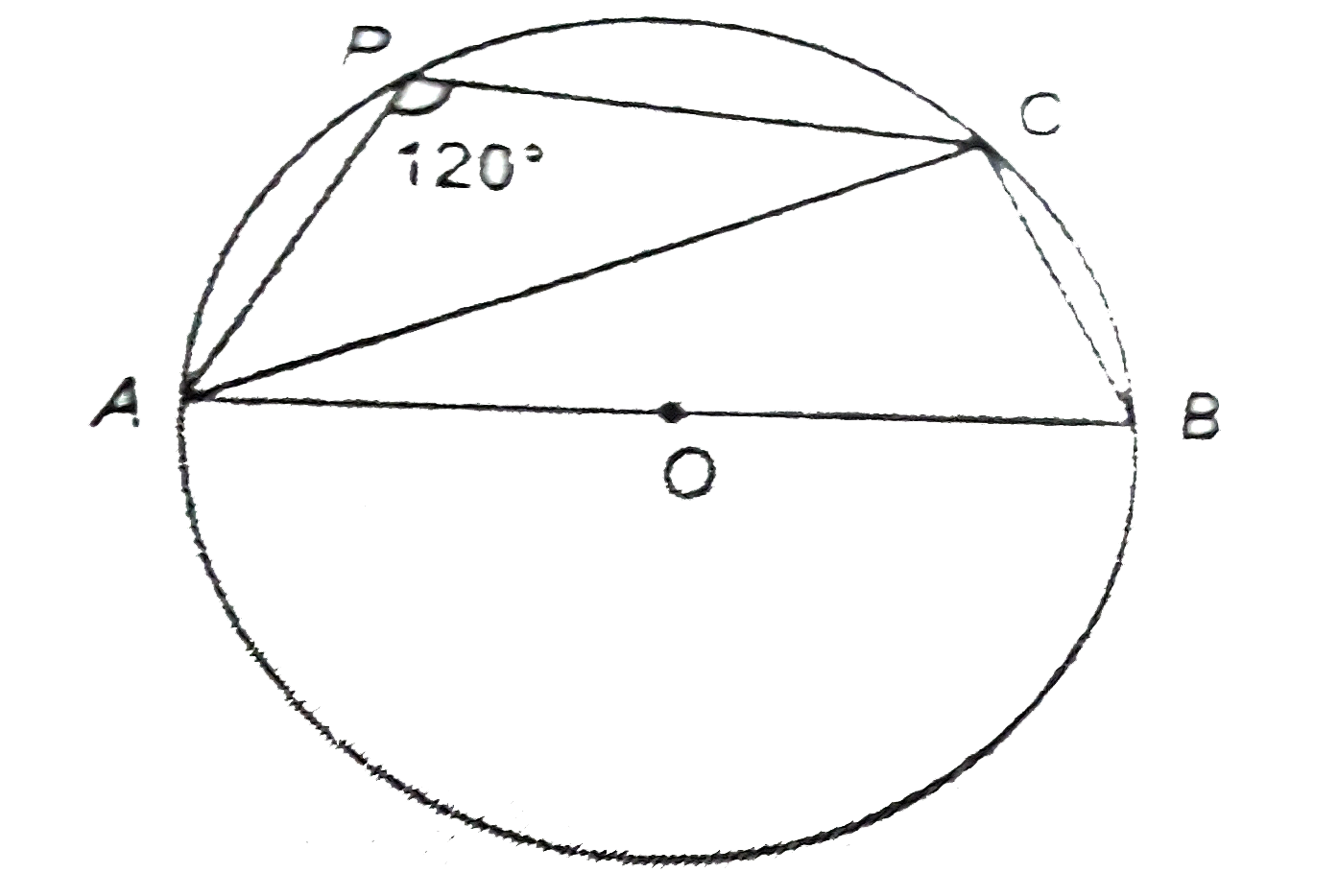
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.
View Solution
