The acceleration of a particle moving in a straight line varies with its displacement as,a=2s+1 veocity o particle is zero at zero displacement. Find the corresponding velocity - displacement equation.
To solve the problem step by step, we need to derive the velocity-displacement equation from the given acceleration-displacement relationship. Here’s the detailed solution:
Step 1: Understand the relationship between acceleration, velocity, and displacement
We know that acceleration a can be expressed as:
a=dvdt
We also know that velocity v can be expressed as:
v=dsdt
Using the chain rule, we can relate acceleration to velocity and displacement:
a=vdvds
Step 2: Substitute the given acceleration expression
The problem states that the acceleration a varies with displacement s as:
a=2s+1
Substituting this into our expression for acceleration gives:
vdvds=2s+1
Step 3: Rearrange the equation for integration
Rearranging the equation, we have:
vdv=(2s+1)ds
Step 4: Integrate both sides
Now we will integrate both sides. The left side integrates from 0 to v and the right side integrates from 0 to s:
∫v0vdv=∫s0(2s+1)ds
Step 5: Perform the integration
1. For the left side:
∫vdv=v22∣∣v0=v22−0=v22
2. For the right side:
∫(2s+1)ds=∫2sds+∫1ds=2⋅s22∣∣s0+s∣∣s0=s2+s−(0+0)=s2+s
Step 6: Set the results equal to each other
Now we equate the results from both integrations:
v22=s2+s
Step 7: Solve for v2
Multiplying both sides by 2 gives:
v2=2(s2+s)
Step 8: Factor the right side
Factoring the right side:
v2=2s(s+1)
Step 9: Take the square root to find v
Taking the square root of both sides gives us the final velocity-displacement equation:
v=√2s(s+1)
Final Answer
The corresponding velocity-displacement equation is:
v=√2s(s+1)
---
We know that acceleration a can be expressed as:
a=dvdt
We also know that velocity v can be expressed as:
v=dsdt
Using the chain rule, we can relate acceleration to velocity and displacement:
a=vdvds
The problem states that the acceleration a varies with displacement s as:
a=2s+1
Substituting this into our expression for acceleration gives:
vdvds=2s+1
Rearranging the equation, we have:
vdv=(2s+1)ds
Now we will integrate both sides. The left side integrates from 0 to v and the right side integrates from 0 to s:
∫v0vdv=∫s0(2s+1)ds
1. For the left side:
∫vdv=v22∣∣v0=v22−0=v22
∫(2s+1)ds=∫2sds+∫1ds=2⋅s22∣∣s0+s∣∣s0=s2+s−(0+0)=s2+s
Now we equate the results from both integrations:
v22=s2+s
Multiplying both sides by 2 gives:
v2=2(s2+s)
Factoring the right side:
v2=2s(s+1)
Taking the square root of both sides gives us the final velocity-displacement equation:
v=√2s(s+1)
The corresponding velocity-displacement equation is:
v=√2s(s+1)
Topper's Solved these Questions
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-1
6 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-2
7 Videos
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-2
89 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Question
1 Videos
Similar Questions
The acceleration (a) of a particle moving in a straight line varies with its displacement (s) as a=2s. The velocity of the particle is zero at zero displacement. Find the corresponding velocity-displacement equation.
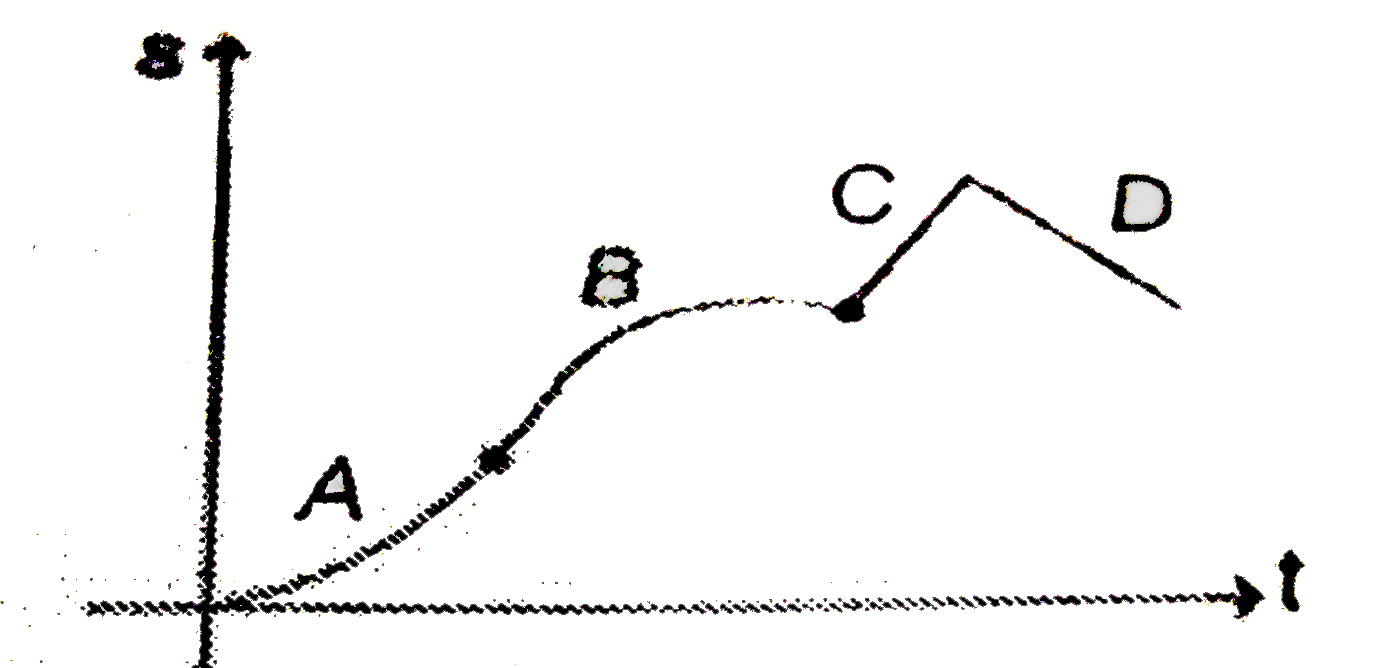
View SolutionDisplacement time graph of a particle moving in a straight line is a shown in figure.
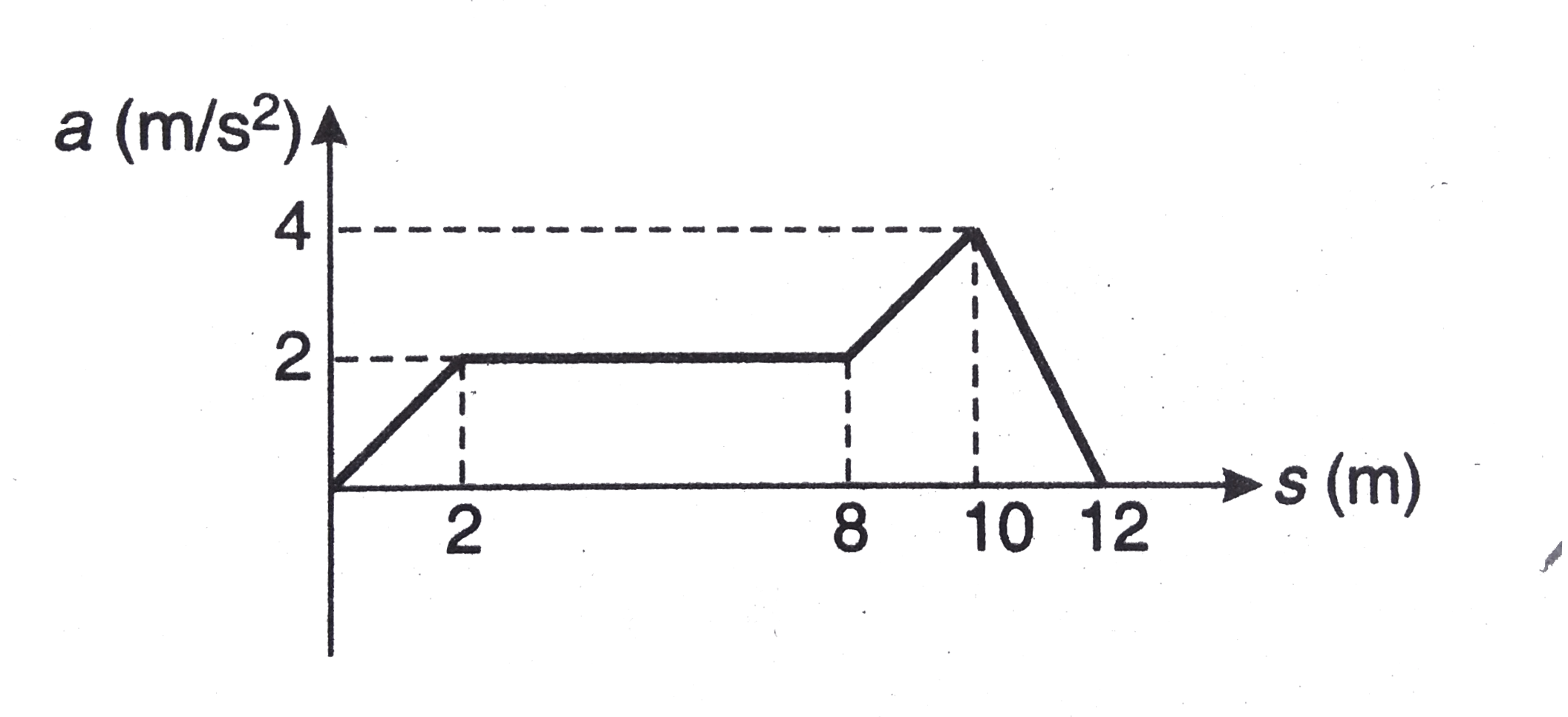
View SolutionThe acceleration-displacement graph of a particle moving in a straight line is as shown in figure, initial velocity of particle is zero. Find the velocity of the particle when displacement of the particle is s=12m.
View SolutionThe power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with the displacement x as :
View SolutionVelocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
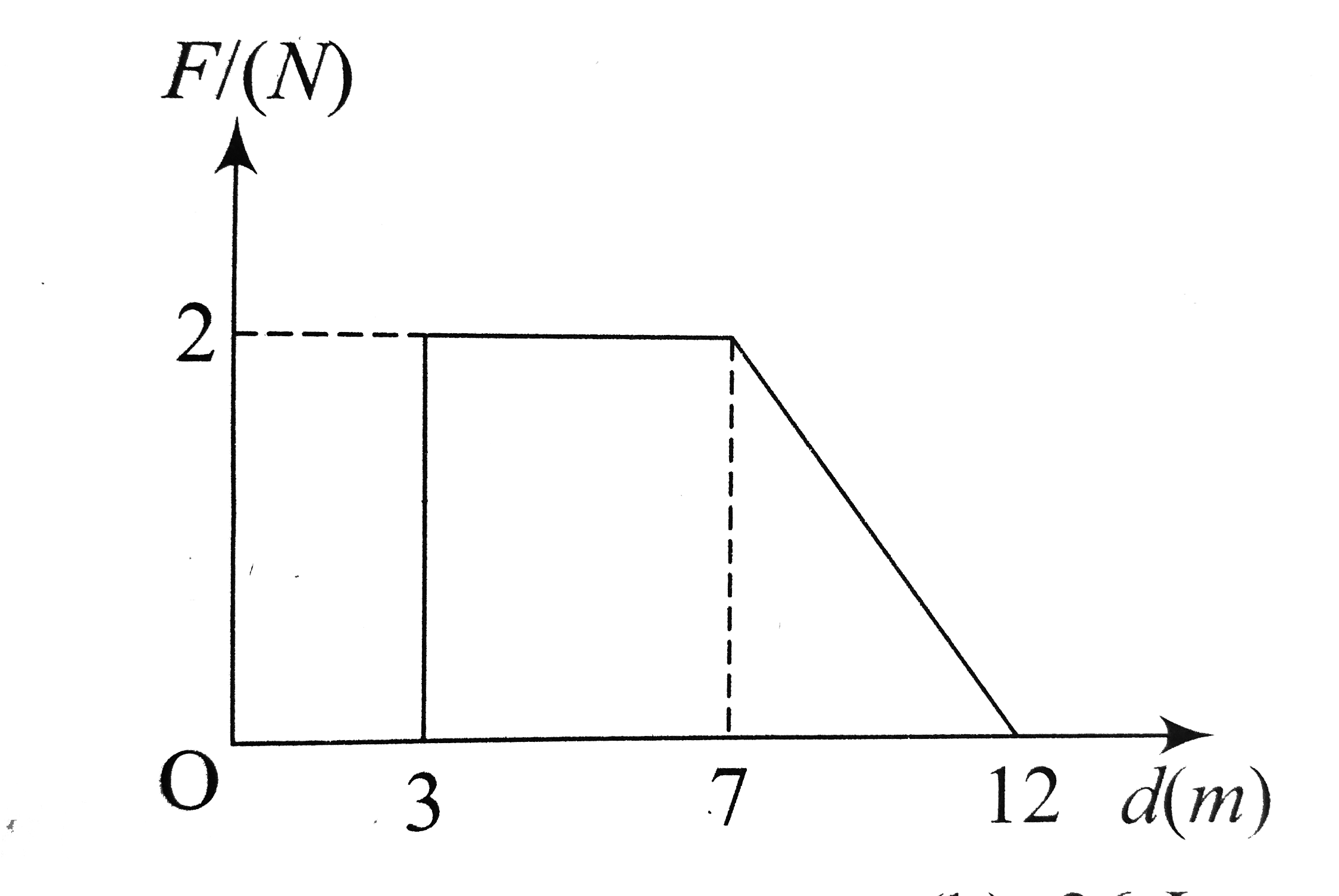
View SolutionForce F on a particle moving in a straight line varies with distance d as shown in the figure. The work done on the particle during its displacement of 12m is
View SolutionIf average velocity of particle moving on a straight line is zero in a time interval, then
View SolutionThe power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with displacement as x1K. Find the value of K.
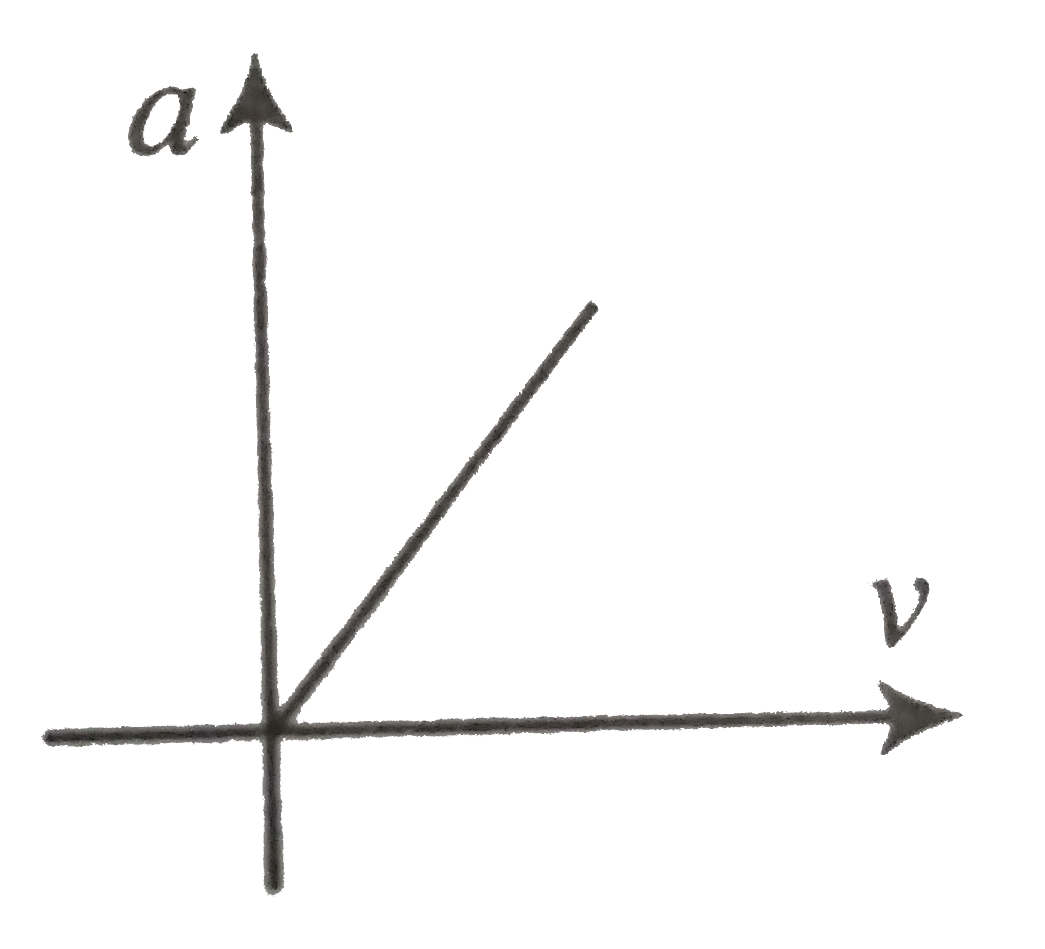
View SolutionThe acceleration - velocity graph of a particle moving in a straight line is shown in figure. Then the slope of the velocity- displacement graph
View SolutionThe velocity-time graph of a particle moving in a staight line is shown in the . Find the displacement and the distance trav elled by the particle in 6s.
 .
.
View Solution
