The acceleration (a) of a particle moving in a straight line varies with its displacement (s) as a=2s. The velocity of the particle is zero at zero displacement. Find the corresponding velocity-displacement equation.
To find the velocity-displacement equation given that the acceleration a of a particle varies with its displacement s as a=2s, and that the velocity is zero at zero displacement, we can follow these steps:
1. Write the relationship between acceleration and displacement:
a=2s
2. Recall that acceleration is the rate of change of velocity:
a=dvdt
3. Use the chain rule to express dvdt in terms of s:
a=dvdt=dvds⋅dsdt
Here, dsdt is the velocity v.
4. Substituting a=2s into the equation:
dvds⋅v=2s
5. Rearranging the equation:
vdv=2sds
6. Integrate both sides:
- The left side integrates to:
∫vdv=v22
- The right side integrates to:
∫2sds=s2
Thus, we have:
v22=s2+C
where C is the constant of integration.
7. Determine the constant C:
Given that the velocity v=0 when s=0:
022=02+C⟹C=0
8. Substituting C back into the equation:
v22=s2
9. Rearranging to find the velocity in terms of displacement:
v2=2s2
Taking the square root of both sides gives:
v=√2s
Final Result:
The corresponding velocity-displacement equation is:
v=√2s
a=2s
a=dvdt
a=dvdt=dvds⋅dsdt
Here, dsdt is the velocity v.
dvds⋅v=2s
vdv=2sds
- The left side integrates to:
∫vdv=v22
- The right side integrates to:
∫2sds=s2
v22=s2+C
where C is the constant of integration.
Given that the velocity v=0 when s=0:
022=02+C⟹C=0
v22=s2
v2=2s2
Taking the square root of both sides gives:
v=√2s
The corresponding velocity-displacement equation is:
v=√2s
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-0237videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-036videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)46videos
KINEMATICS-2D
- BOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)4videos
NEWTON'S LAWS OF MOTION & FRICTION
Similar Questions
Knowledge Check
- Question 1 - Select One
Acceleration (a)-displacement(s) graph of a particle moving in a straight line is shown here. The initial velocity of the particle is zero. The v-s graph of the particle would be
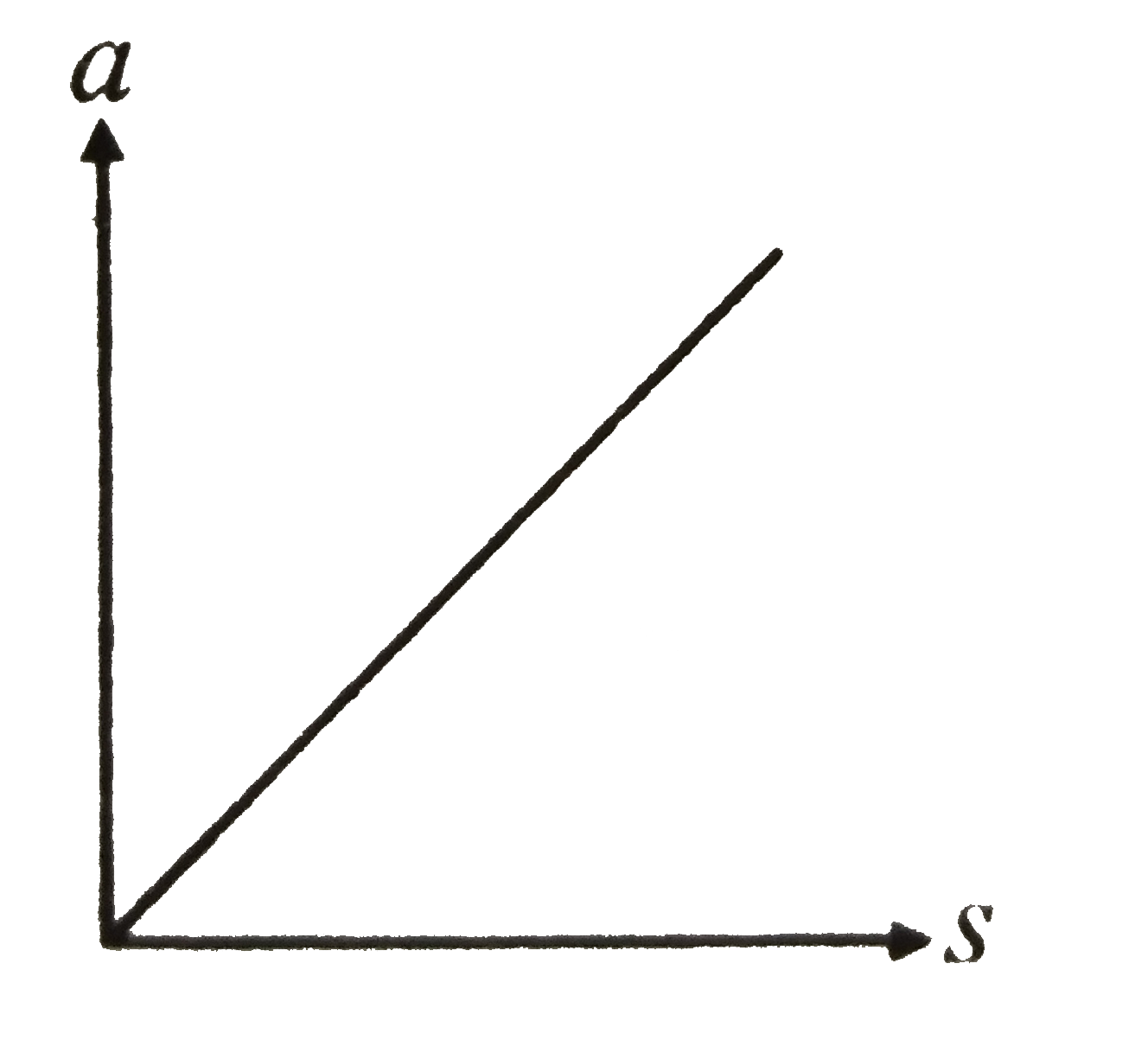 A
A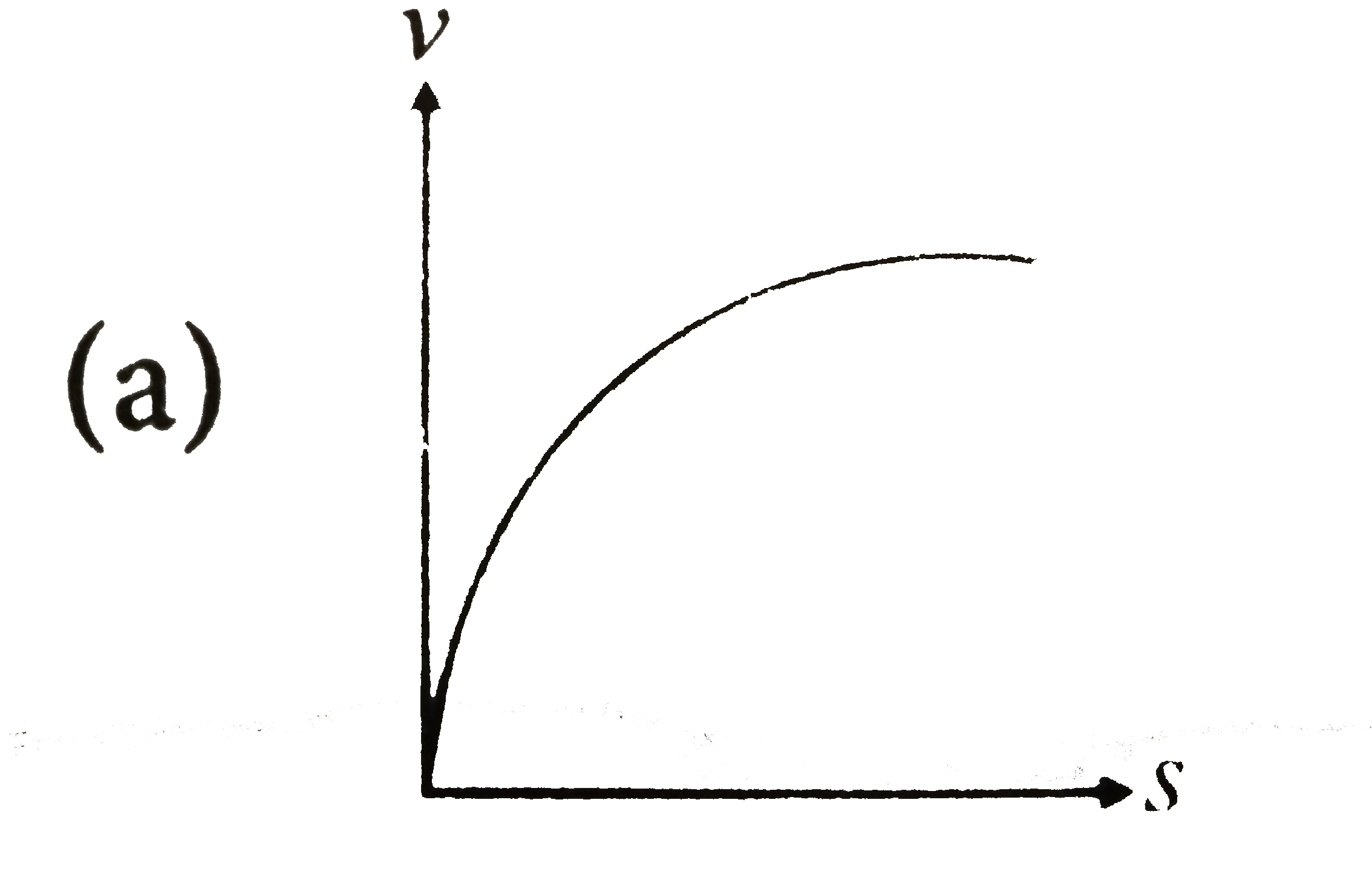 B
B C
C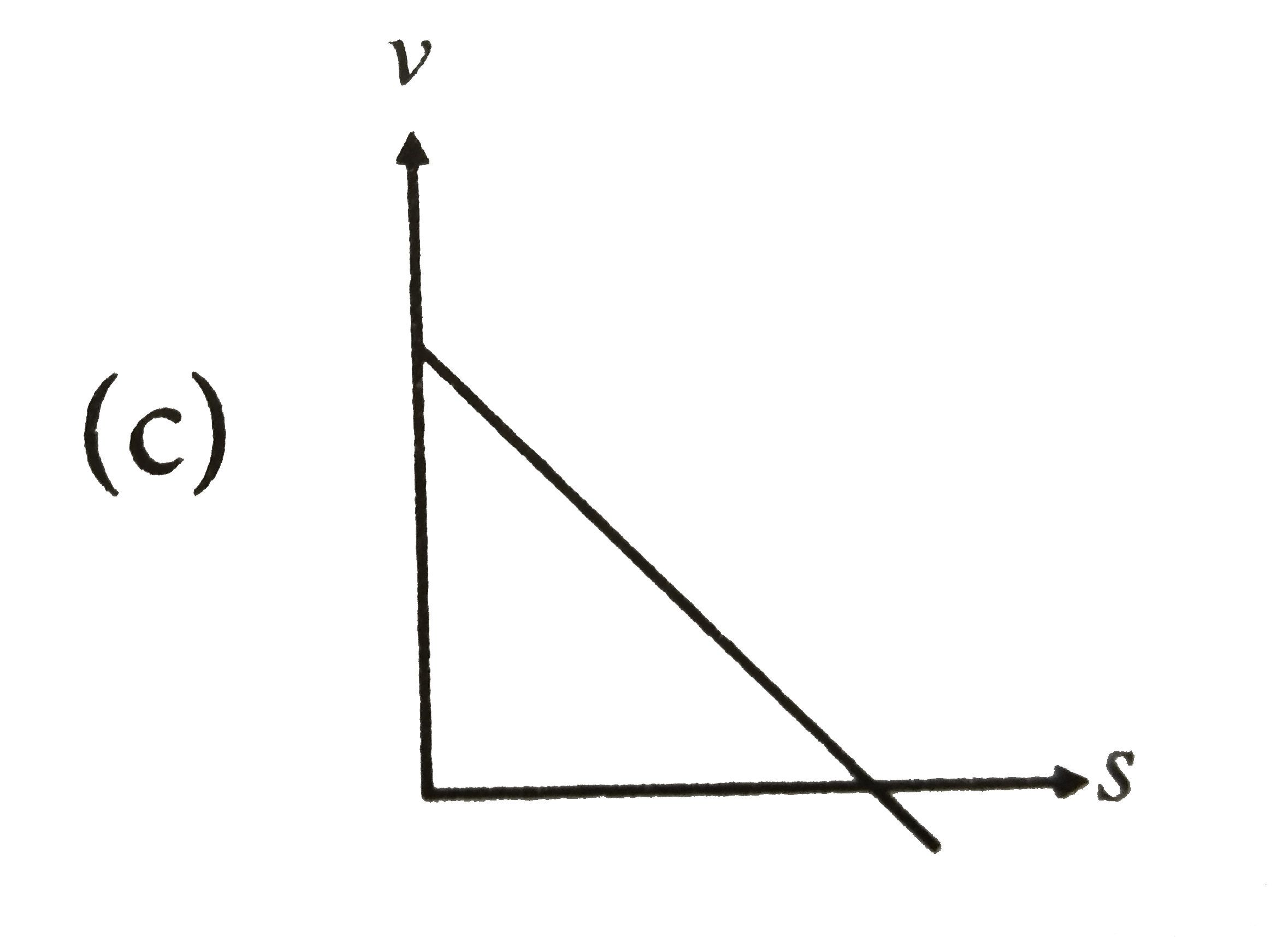 D
D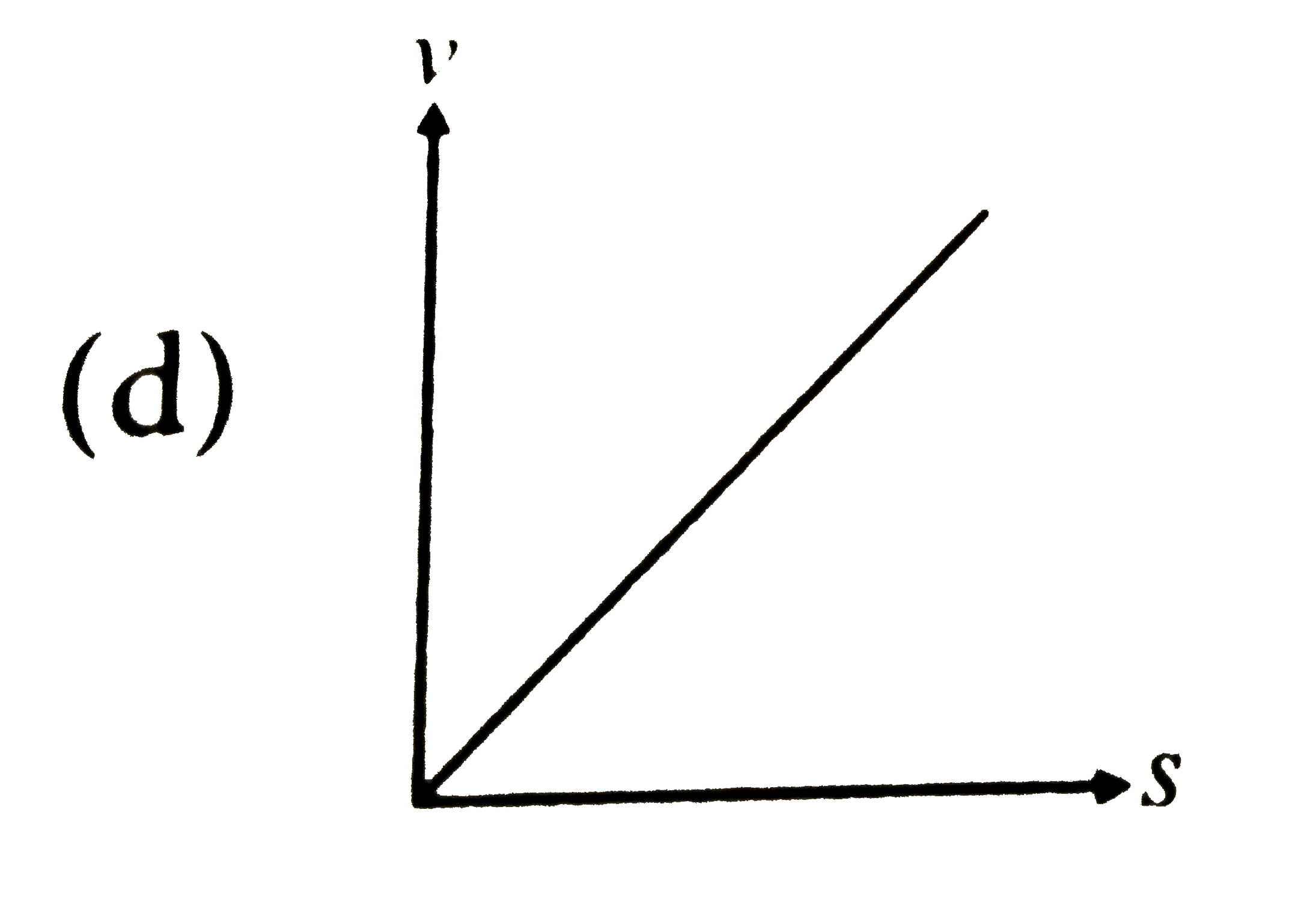
The power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with the displacement x as :
View SolutionDisplacement time graph of a particle moving in a straight line is a shown in figure.
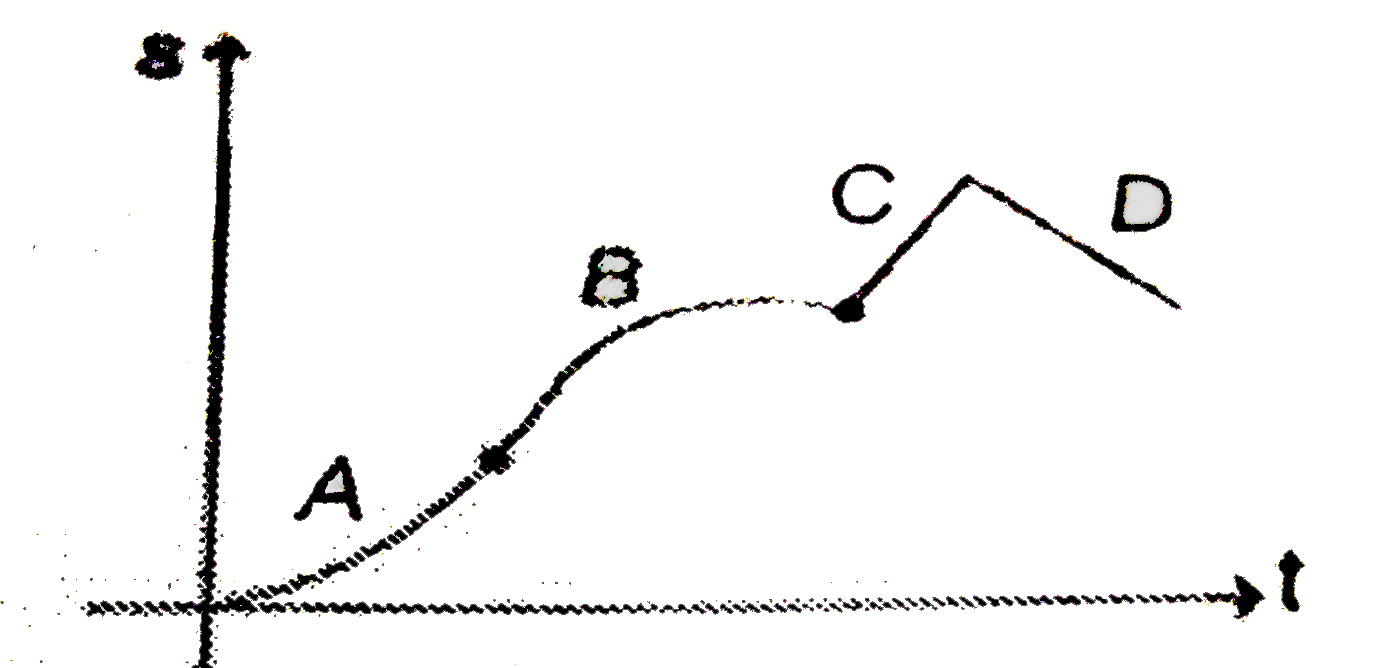 View Solution
View SolutionThe power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with displacement as x1K. Find the value of K.
View SolutionForce F on a particle moving in a straight line varies with distance d as shown in the figure. The work done on the particle during its displacement of 12m is
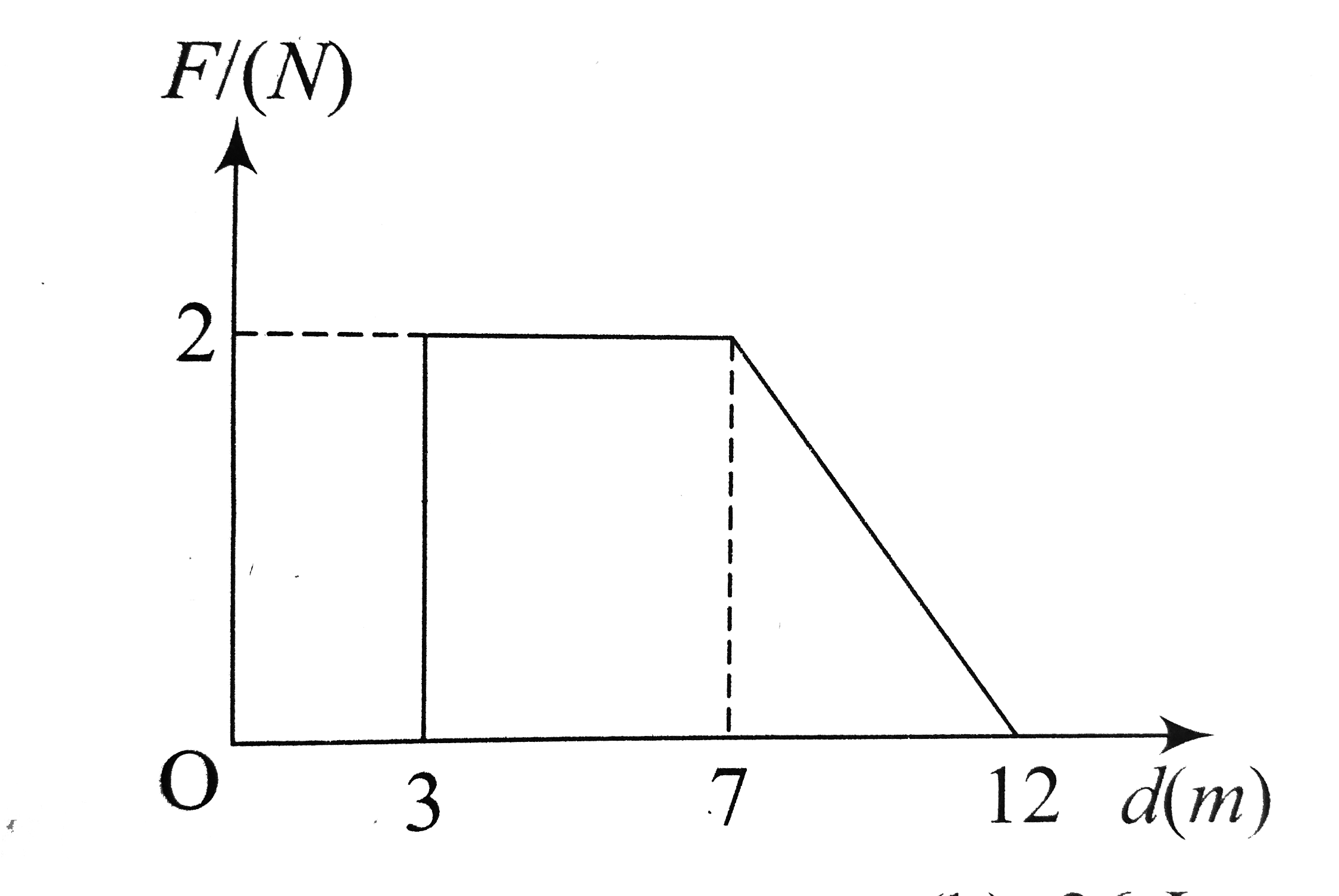 View Solution
View SolutionVelocity displacement graph of a particle moving in a straight line is as shown in figure.
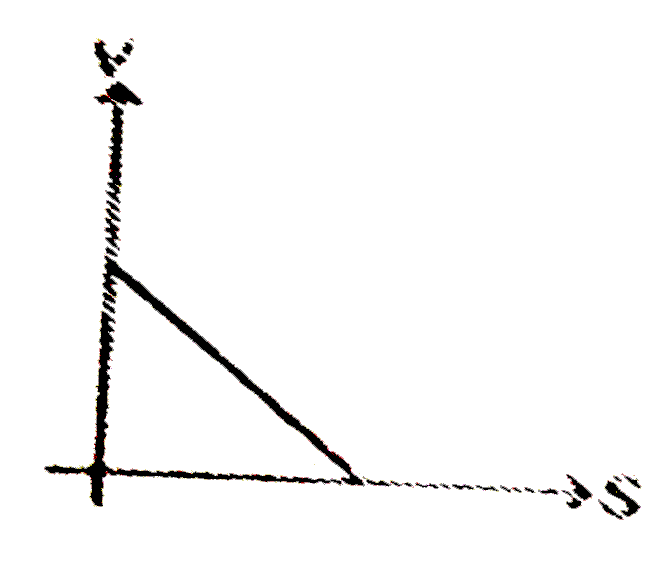 View Solution
View SolutionThe acceleration - velocity graph of a particle moving in a straight line is shown in figure. Then the slope of the velocity- displacement graph
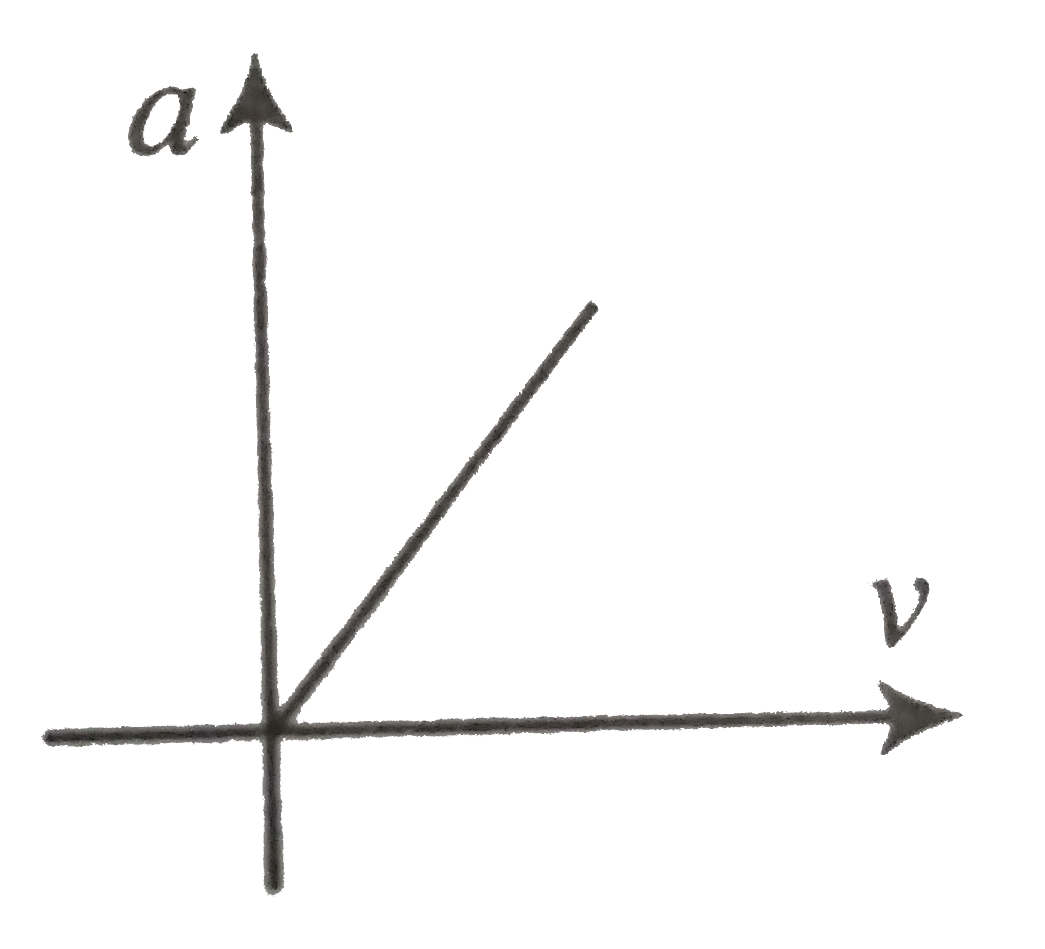 View Solution
View SolutionThe velocity-time graph of a particle moving in a staight line is shown in the . Find the displacement and the distance trav elled by the particle in 6s.
 .View Solution
.View Solution

