The distance travelled by a particle in time t is given by s=(2.5ms2)t2. Find a. the average speed of the particle during the time 0 to 5.0 s, and b. the instantaneous speed ast t=5.0 is
(a) The distance travelled during time 0 to 5.0 s is,
S=(2.5)(5.0)2=62.5 m
The average speed during this time is
vavg=distance travelledtime taken=62.55=12.5m/s
(b) Given S=(2.5)t2
Intantaneous speed = dSdt=ddt(2.5t2)=(2.5)(2t)=5t
∴ At t=5.0s the speed is
[v]t=5S=(5.0)×(5.0)=25m/s
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-32videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-46videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-16videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-289videos
KINEMATICS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Question1videos
MISCELLANEOUS
Similar Questions
The distance s of a particle in time t is given by s=t3−6t2−4t−8. Its acceleration vanishes at t=
View SolutionThe distance covered by an object (in meter) is given by
s=8t3−7t2+5t
Find its speed at t = 2 s.View SolutionThe displacement (in metre) of a particle moving along X-axis is given by x=18t+5t2. The average acceleration during the interval t1=2s and t2=4s is
View SolutionFigure shows the speed versus time graph for a particle. Find the distance travelled by the particle during the time t=0 to t=3s.
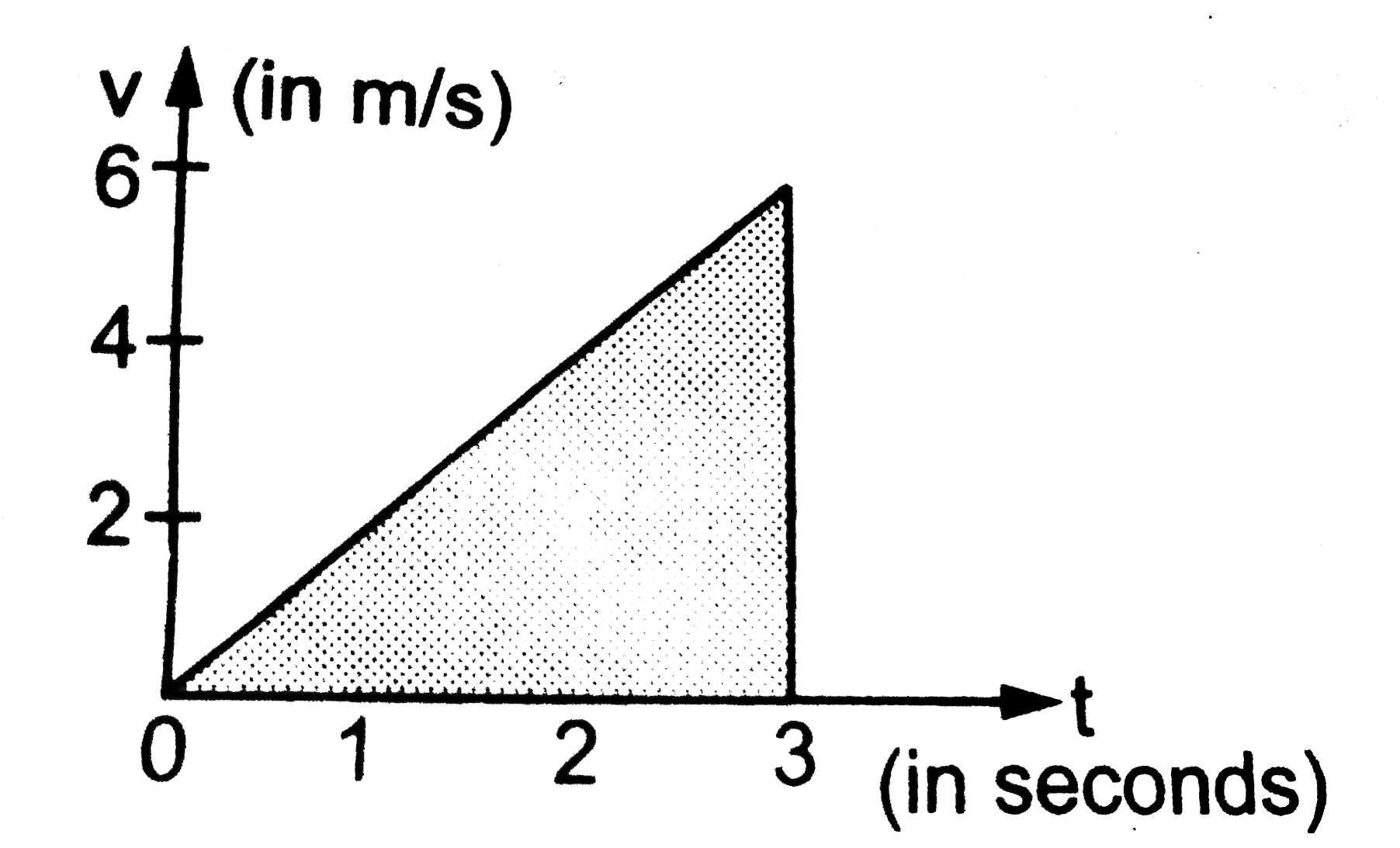 View Solution
View SolutionThe position (x) - time (t) graph for a particle moving along a straight line is shown in figure. The average speed of particle in time interval t = 0 to t = 8 s is
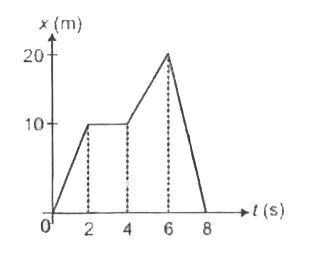 View Solution
View SolutionFig. shows the graph of the x-coordinate of a particle going along the x-axis as a function of time. Find (a) the average velocity during 0 to 10s, (b) instantaneous velocity at 2, 5, 8 and 12s.
 View Solution
View SolutionFigure shows the graph of the x-coordinaste of a particle going along the X-axis as a function of time.Find a. te average velocity during 0 to 10s, b. instantaneous velocity at 2,5,8 and 12s.
 View Solution
View SolutionThe acceleration of a particle is given by a (t)=(3.00 m/s2−(2.00ms3))t. (a) Find the initial speed v0 such that the particle will have the same x -coordinate at t =5.00 as it had at t=0. (b)What will be the velocity at t =5.00s?
View SolutionAcceleration of a particle is given by
a=3t2+2t+1
Where t is time . Find
(i) its velocity at time t assuming velocity to be 10 m/s at t = 0.
(ii) its position at time t assuming that the particle is at origin at t = 0.
(iii) What is the average speed of the particle in the duration t = 0 to t = 1s?
(iv) What is the average acceleration of the particle in the duration t = 0 to t = 1s?View SolutionThe velocity of a particle is given by v=(2t2−3t+10)ms−1. Find the instantaneous acceleration at t = 5 s.
View Solution

