Given KE=12mv2. If m=10kg,v=5m/s then find the value of KE?
The correct Answer is:125 J
To find the kinetic energy (KE) of an object, we can use the formula:
KE=12mv2
Where:
- m is the mass of the object,
- v is the velocity of the object.
Given:
- m=10kg
- v=5m/s
Now, we will substitute the values of m and v into the formula.
Step 1: Substitute the values into the formula
KE=12×10kg×(5m/s)2
Step 2: Calculate v2
First, calculate (5m/s)2:
(5m/s)2=25m2/s2
Step 3: Substitute v2 back into the equation
Now substitute v2 back into the equation:
KE=12×10kg×25m2/s2
Step 4: Calculate 12×10
Calculate 12×10:
12×10=5
Step 5: Multiply by 25m2/s2
Now multiply:
KE=5×25kg⋅m2/s2
Step 6: Calculate the final value
KE=125J
Thus, the kinetic energy of the object is:
125J
- m is the mass of the object,
- v is the velocity of the object.
- m=10kg
- v=5m/s
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (VECTORS)
60 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Units, Dimensions & Measurements)
30 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Graphs))
29 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
The block of mass m1 is placed on a wedge of an angle θ, as shown. The block is moving over the inclined surface of the wedge. Friction coefficient between the block and the wedge is μ1, whereas it is μ2 between the wedge and the horizontal surface. if μ1=12,θ=45∘,m1=4kg,m2=5kg and g=10m/s2, find minimum value of μ2 so that the wedge remains stationary on the surface. express your answer in multiple of 10−3
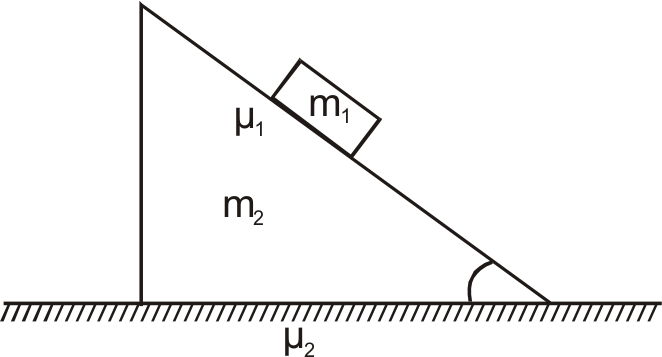
View SolutionThe block of mass m1 is placed on a wedge of an angle θ, as shown. The block is moving over the inclined surface of the wedge. Friction coefficient between the block and the wedge is μ1, whereas it is μ2 between the wedge and the horizontal surface. if μ1=12,θ=45∘,m1=4kg,m2=5kg and g=10m/s2, find minimum value of μ2 so that the wedge remains stationary on the surface. express your answer in multiple of 10−3

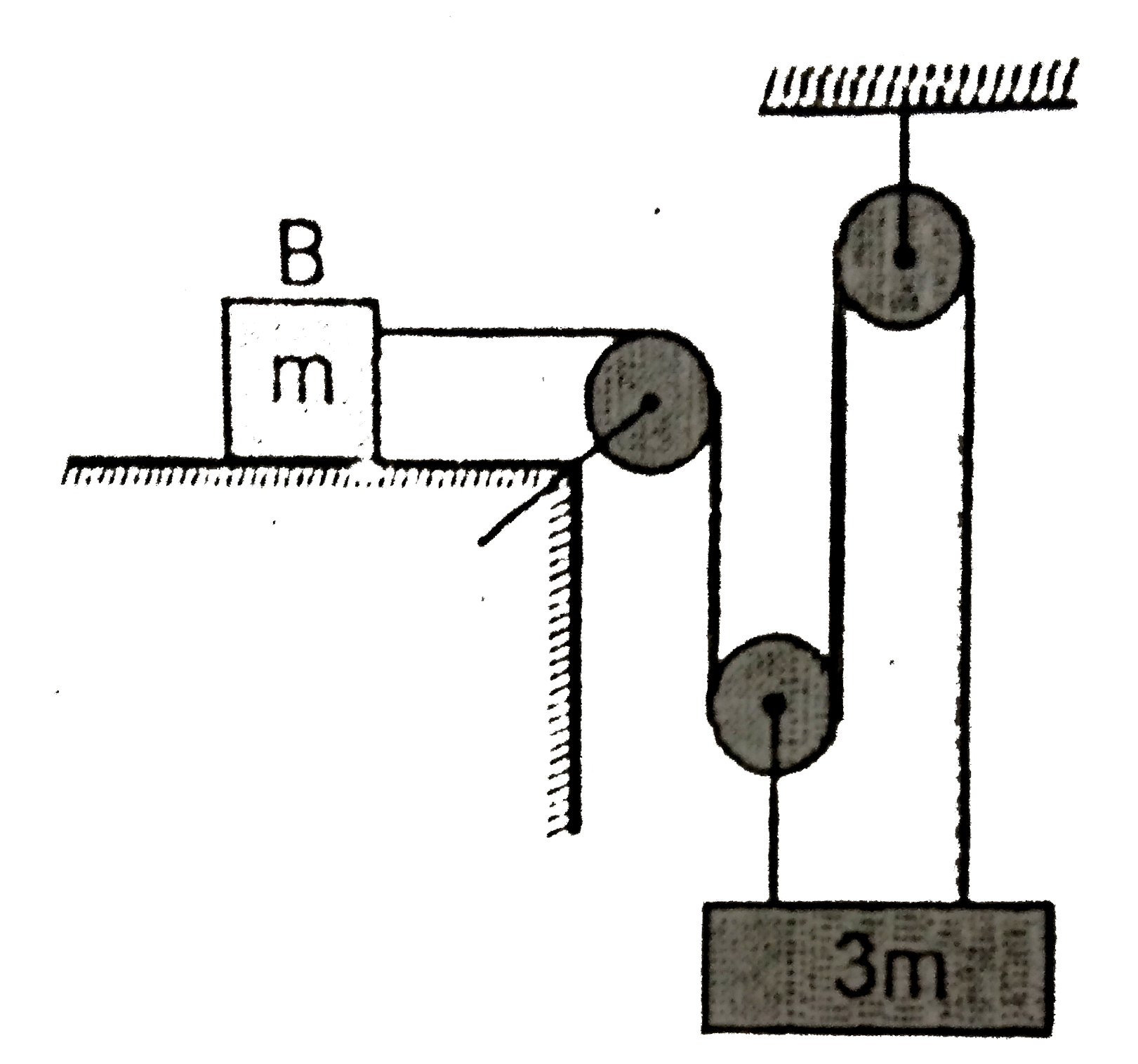
View SolutionIf the acceleration of the block B in the following system is a ( in m/s2) then find out value of 2a/5(g=10m/s2):
View SolutionGiven Y=2×1011N/m2,ρ=104kg/m3
Find out elongation in rod.

View SolutionTwo blocks A and B are connected by a string as shown as shown in the figure . Friction coefficient of the inclined plane is 0.5 . The mass of the block A is 5 kg. If minimum and maximum values of mass of the block B for which the block A remains in equilibrium are m1andm2 then find the value of (m2−m1) [in kg]

View SolutionIn the arrangement shown in the diagram, pulleys are small and springs are ideal. k1=k2=k3=k4=10Nm−1 are force constants of the springs and mass m=10kg. If the time period of small vertical oscillations of the block of mass m is given by 2πx seconds, then find the value of x.

View SolutionA conservative force acts on a 4 kg particle in x direction. The potential energy U(x) is given by U(X)=40+(x–6)2, where x is in metre. If it is given that at x = 8 m, KE is 30 J then find the maximum KE of the particle.
View SolutionThe mass m of a body moving with a velocity v is given by m=m0√1−v2c2 where m0 = rest mass of body =10kg and c = speed of light =3×108m/s. Find the value of m at v=3×107m/s
View SolutionIn a horizontal pipeline of uniform cross section the pressure falls by 8N/m2 between two points separated by 1km. If oil of density 800kg/m3 flows through the pipe, find the change in KE per kg of oil at these points.
View SolutionIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
Find the tension in the string
View Solution
