Two thermometers 'X' & 'Y' shows boiling point & freezing point of water as 220∘X & 20∘X and 120∘Y & −40∘Y respectively. If 'X' shows 100∘X. then find the reading in Y thermomter.
25∘Y
50∘Y
20∘Y
24∘Y
The correct Answer is:D
To solve the problem, we will use the concept of linear interpolation between the freezing and boiling points of the two thermometers.
1. Identify the Fixed Points:
- For thermometer X:
- Freezing point: 20∘X
- Boiling point: 220∘X
- For thermometer Y:
- Freezing point: −40∘Y
- Boiling point: 120∘Y
2. Set Up the Formula:
We can use the formula for converting temperatures between the two scales:
TX−TXminTXmax−TXmin=TY−TYminTYmax−TYmin
Where:
- TX is the temperature in thermometer X.
- TY is the temperature in thermometer Y.
- TXmin=20∘X
- TXmax=220∘X
- TYmin=−40∘Y
- TYmax=120∘Y
3. Substituting Known Values:
Given that TX=100∘X:
100−20220−20=TY−(−40)120−(−40)
Simplifying the left side:
80200=TY+40160
This simplifies to:
25=TY+40160
4. Cross-Multiplying:
Cross-multiplying gives:
2×160=5(TY+40)
Which simplifies to:
320=5TY+200
5. Solving for TY:
Rearranging the equation:
5TY=320−200
5TY=120
TY=1205=24
6. Final Answer:
Therefore, the reading in thermometer Y is:
TY=24∘Y
Conclusion:
The reading in thermometer Y when thermometer X shows 100∘X is 24∘Y.
- For thermometer X:
- Freezing point: 20∘X
- Boiling point: 220∘X
- For thermometer Y:
- Freezing point: −40∘Y
- Boiling point: 120∘Y
We can use the formula for converting temperatures between the two scales:
TX−TXminTXmax−TXmin=TY−TYminTYmax−TYmin
Where:
- TX is the temperature in thermometer X.
- TY is the temperature in thermometer Y.
- TXmin=20∘X
- TXmax=220∘X
- TYmin=−40∘Y
- TYmax=120∘Y
Given that TX=100∘X:
100−20220−20=TY−(−40)120−(−40)
Simplifying the left side:
80200=TY+40160
This simplifies to:
25=TY+40160
Cross-multiplying gives:
2×160=5(TY+40)
Which simplifies to:
320=5TY+200
Rearranging the equation:
5TY=320−200
5TY=120
TY=1205=24
Therefore, the reading in thermometer Y is:
TY=24∘Y
The reading in thermometer Y when thermometer X shows 100∘X is 24∘Y.
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Thermal Physics) (Calorimetry)
14 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Thermal Physics) (Mode of Heat Transfer)
14 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Surface Tension)
26 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
The freezing point of water on a thermometer is marked as 20unit and the boiling point as 120 unit. Find the value of temperature 80∘C on this thermometer.
View SolutionPoints A and B have co-ordinates (3, 5) and (x, y) respectively. The mid-point of AB is (2, 3). Find the values of x and y.
View Solution
Knowledge Check
The temporary hardness of a water sample is due to compound X. Boiling this sample converts X to compound Y. X and Y, respectively, are :
AMg(HCO3)2 and MgCO3BCa(HO3)2 and CaOCCa(HCO3)2 and Ca(OH)2DMg(HCO3)2 and Mg(OH)2
If the angles of a triangle are x, y and 40∘ and the difference between the two angles x and y is 30∘. Then, find the value of x and y.
View SolutionIn a termperature scale X ice point of water is assigned a value of 20∘X and the boiling point of water is assiggned a value of 220∘X. In another scale Y the ice poiny of water is assigned a value of −20∘Y and the boiling point is given a value of 380∘Y. Then temperature on both the scales will be same is
View SolutionThe temporary hardness of a water sample is due to compound X. Boiling this sample converts X to compound Y. X and Y, respectively, are :
View SolutionFigure shows electric lines of force. If Ex and Ey are the magnitudes of electric field at points x and y respectively, then
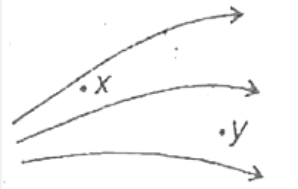
View SolutionOn an X temperature scale, water freezes at −125.0∘X and boils at 375.0∘X. On a Y temperature scale, water freezes at −70.0∘Y and boils at −30.0∘Y. The value of temperature on X-scale equal to the temperature of 50.0∘Y on Y-scale is
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid=points of sides AB and DC respectively. Show that AXCY is a parallelogram. Figure
View SolutionIf P(x,y) is any point on the line joining the point A(a,0)andB(0,b), then show that xa+yb=1.
View Solution
