A particle of mass 4kg moves simple harmonically such that its PE (U) varies with position x, as shown. The period of oscillations is
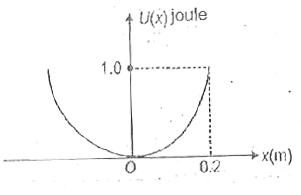
2π25s
π√25
4π5s
2π√25s
The correct Answer is:D
Step by step video solution for A particle of mass 4kg moves simple harmonically such that its PE (U) varies with position x, as shown. The period of oscillations is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Oscillations) (Simple pendulum and types of SHM)
17 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Fundamental)
25 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Dscillations) (Kinematics of SHM)
20 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
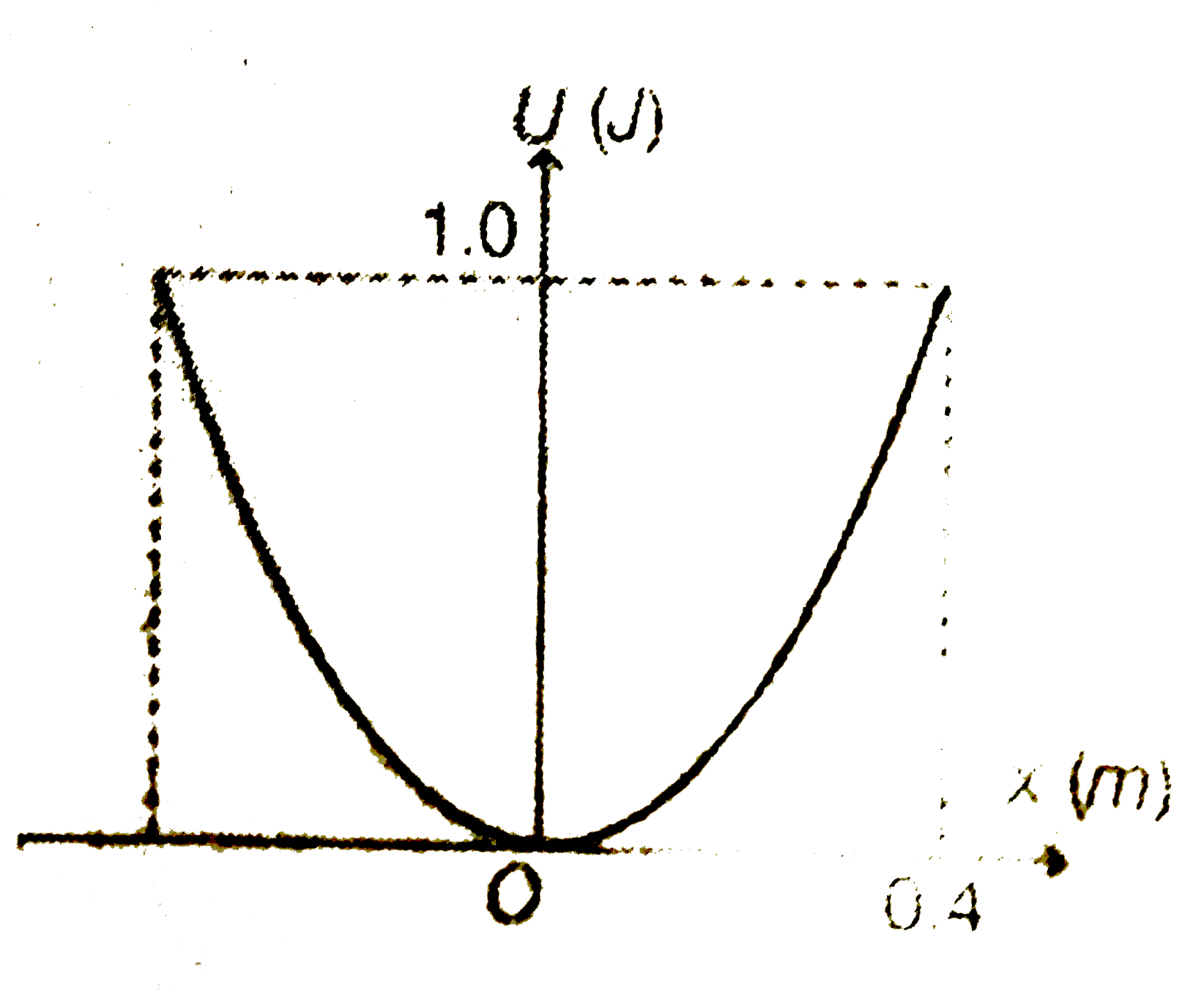
A particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View SolutionA particle of mass = 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is nπ5 second. Find value of n.
View SolutionThe variation of force (F) acting on a particle of mass 800 g with position (x) is as shown in figure. The time period of oscillation of the particles is
View SolutionA particle of mass 0.50 kg executes a simple harmonic motion under a force F=−(50Nm−1)x. If it crosses the centre of oscillation with a speed of 10ms−1, find the amplitude of the motion.
View SolutionThe variations of potential energy (U) with position x for three simple harmonic oscillators A, B and C are shown in figure. The oscillators have same mass. The time period of oscillation is greatest for

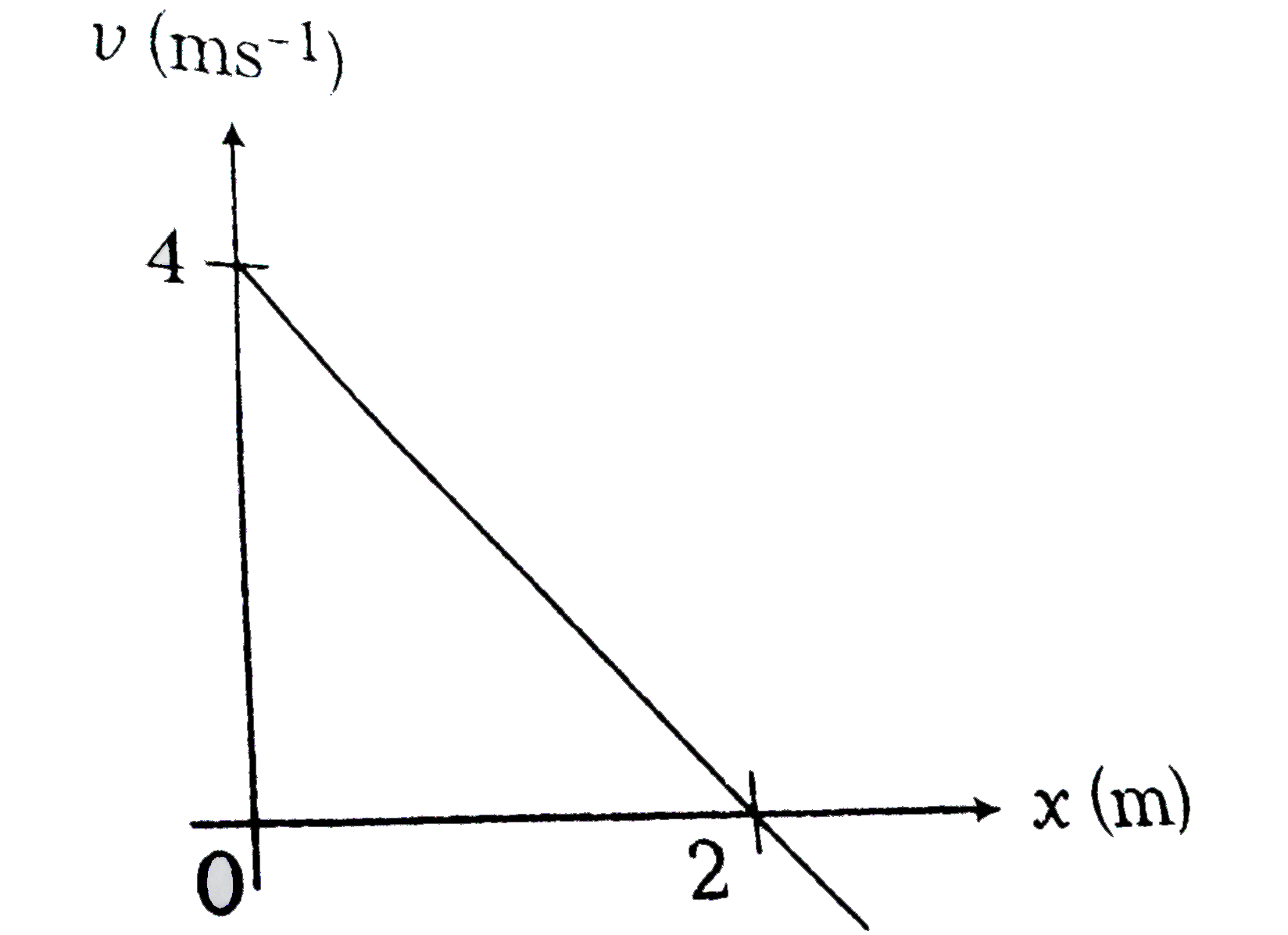
View SolutionThe velocity (υ) of a particle moving along X-axis varies with its position x as shown in figure. The acceleration (a) of particle varies with position (x) as
View SolutionA particle executes simple harmonic oscillation with an amplitudes a. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude from the equilibrium position is
View SolutionA particle executes simple harmonic oscillation with an amplitudes a. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude from the equilibrium position is
View SolutionA particle of mass m=1kg oscillates simple harmonically with angular frequency 1rad/s. Find the phase of the particle at t=1sand2s. Start calculating time when the particle moves up passing through the mean position.
View Solution
