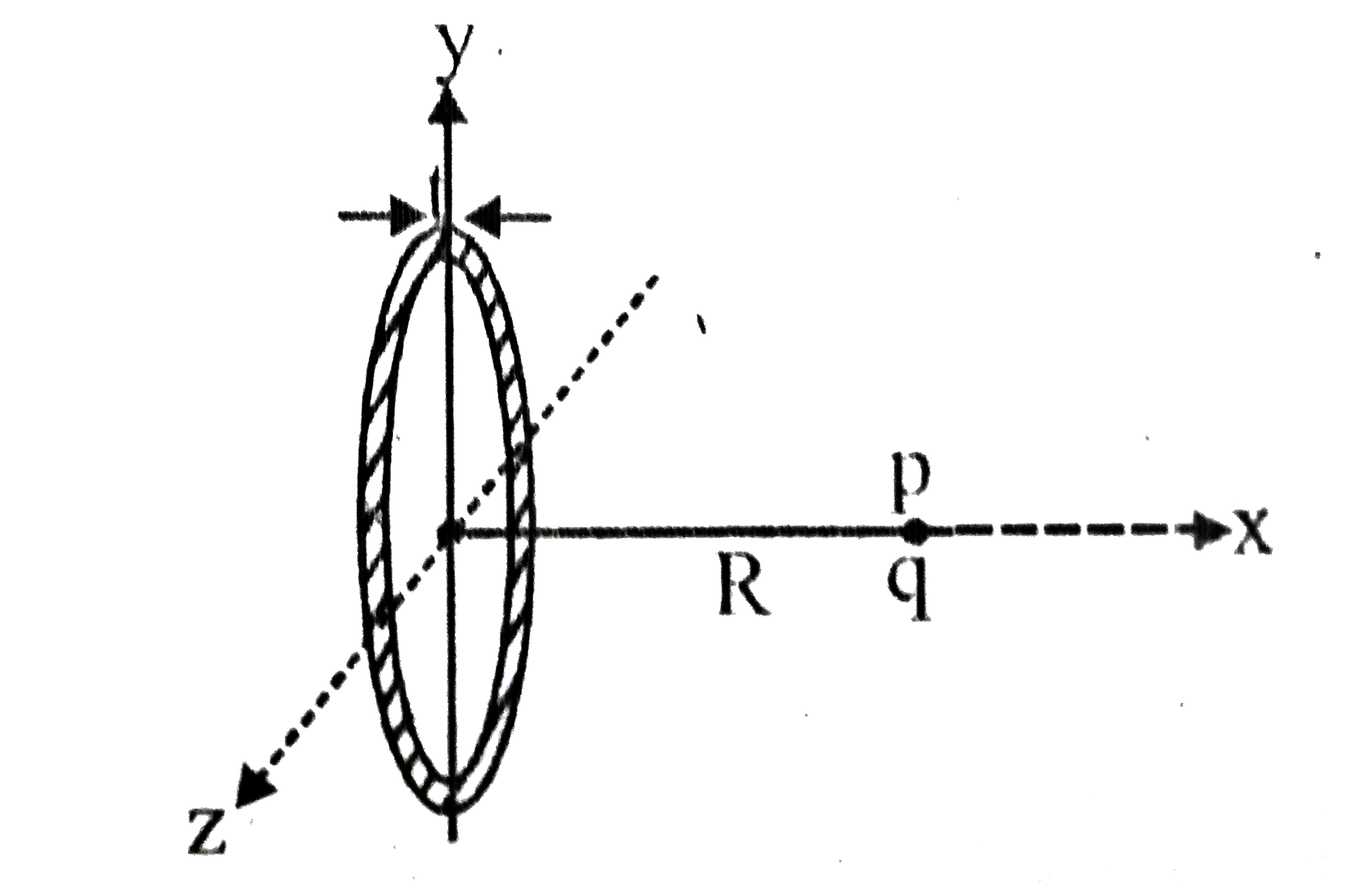
A charge q is placed at the point P as shown in figure on the axis of the ring of elemental thickness 't' and radius R then flux through the ring is :-
Zero
q2√2ε0(√2−1)
qt4√2ε0R
qt2√2ε0R
The correct Answer is:C
dϕ=EdScosθ
=Kq2R2(2πRt)1√2
Topper's Solved these Questions
Similar Questions
A constant force F is applied at the top of a ring as shown in figure. Mass of the ring is M and radius is R. Angular momentum of particle about point of contact at time t

View SolutionIn the figure shown, the magnet is pushed towards the fixed ring along the axis of the ring and it passes through the ring.
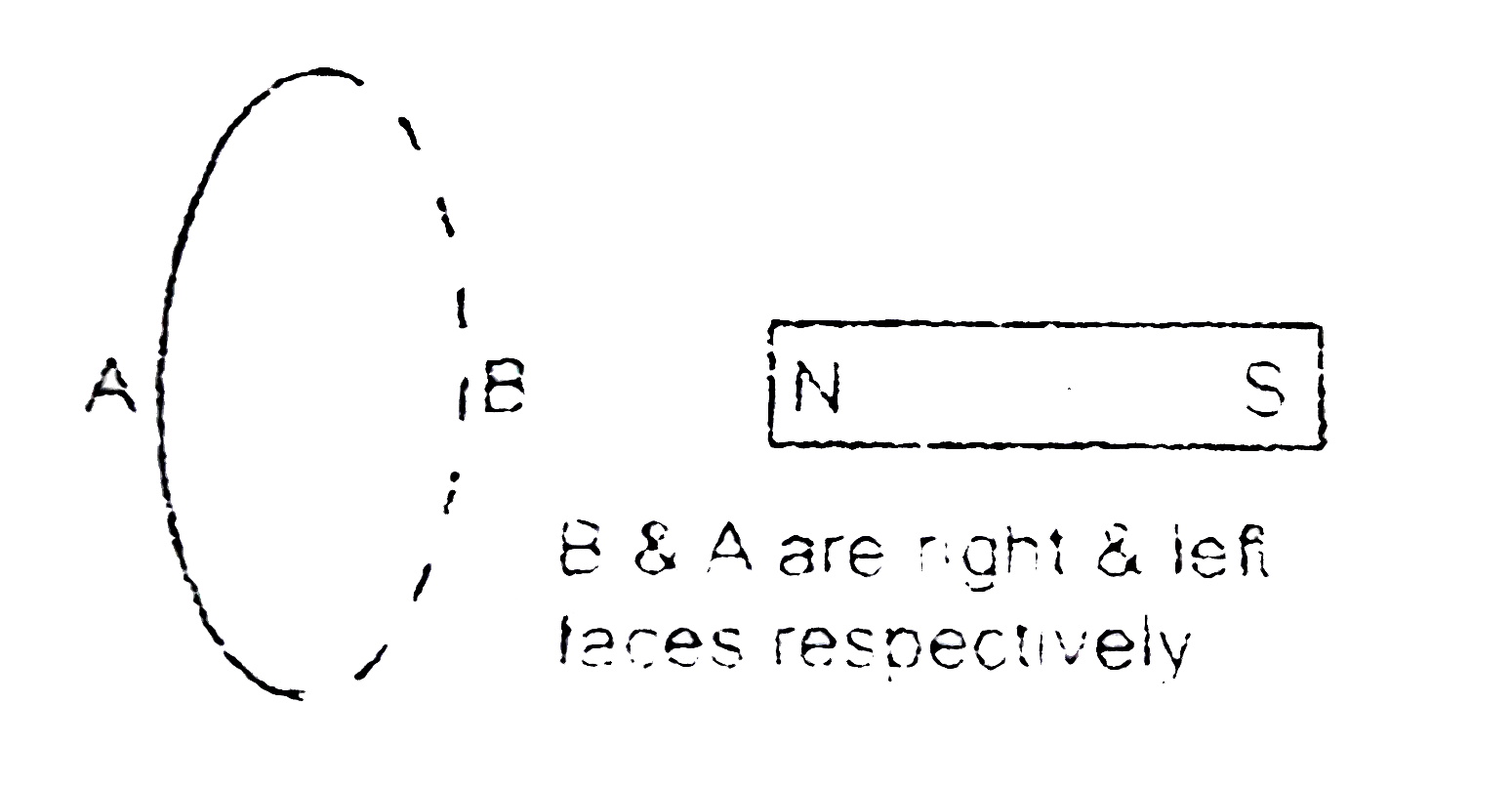
View SolutionFind potential at a point 'P' at a distance 'x' on the axis away from centre of a uniform ring of mass M and radius R .
View SolutionA charge 'Q' is placed at the centre of a hemispherical surface of radius 'R'. The flux of electric field due to charge 'Q' through the surface of hemisphere is
View SolutionA point charge q0 is placed at the centre of uniformly charges ring of total charge Q and radius R. If the point charge is slightly displaced with negligible force along axis of the ring then find out its speed when it reaches a large distance.
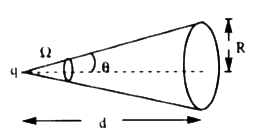
View SolutionA point charge q is placed at a distance d from the centre of a circular disc of radius R. Find electric flux flowing through the disc due to that charge
View SolutionA long solenoid of radius R carries a time (t) – dependent current I=I0(t−2t2) A circular ring of radius = R is placed near the centre of the solenoid and plane of ring makes an angle 30∘ with the axis of solenoid. The time at which magnetic flux through the ring is maximum is :
View SolutionA long solenoid of radius R carries a time (t) – dependent current I=I0(t−2t2) A circular ring of radius = R is placed near the centre of the solenoid and plane of ring makes an angle 30∘ with the axis of solenoid. The time at which magnetic flux through the ring is maximum is :
View SolutionA ring of radius R has charge −Q distributed uniformly over it. Calculate the charge that should be placed at the center of the ring such that the electric field becomes zero at apoint on the axis of the ring at distant R from the center of the ring.
View SolutionA ring of radius R carries a uniformly distributed charge +Q. A point charge −q is placed on the axis of the ring at a distance 2R from the centre of the ring and released from rest. The particle executes a simple harmonic motion along the axis of the ring. State True or False.
View Solution
