If uniform electric field →E=E0ˆi+2E0ˆj, where E0 is a constant exists in a region of space and at (0,0) the electric potential V is zero, then the potential at (x0,2x0) will be -
zero
−5E0x0
−3E0x0
−√5E0x0
The correct Answer is:B
To solve the problem, we need to find the electric potential at the point (x0,2x0) given the uniform electric field →E=E0^i+2E0^j and that the potential V at the point (0,0) is zero.
1. Understand the Electric Field and Potential Relation:
The potential difference ΔV between two points in an electric field is given by:
ΔV=V(B)−V(A)=−∫BA→E⋅d→r
where A is the starting point and B is the ending point.
2. Identify the Points:
Let point A be (0,0) and point B be (x0,2x0). The potential at point A is given as V(0,0)=0.
3. Set Up the Integral:
The differential displacement vector d→r can be expressed as:
d→r=dx^i+dy^j
The electric field →E is given as:
→E=E0^i+2E0^j
4. Calculate the Dot Product:
The dot product →E⋅d→r is:
→E⋅d→r=(E0^i+2E0^j)⋅(dx^i+dy^j)=E0dx+2E0dy
5. Set Up the Integral for Potential:
The potential at point B can be calculated as:
V(x0,2x0)=V(0,0)−∫(x0,2x0)(0,0)→E⋅d→r
Since V(0,0)=0, we have:
V(x0,2x0)=−∫x00E0dx−∫2x002E0dy
6. Evaluate the Integrals:
- For the first integral:
−∫x00E0dx=−E0(x)x00=−E0x0
- For the second integral:
−∫2x002E0dy=−2E0(y)2x00=−2E0(2x0)=−4E0x0
7. Combine the Results:
Now, adding both contributions:
V(x0,2x0)=−E0x0−4E0x0=−5E0x0
Final Result:
Thus, the potential at the point (x0,2x0) is:
V(x0,2x0)=−5E0x0
The potential difference ΔV between two points in an electric field is given by:
ΔV=V(B)−V(A)=−∫BA→E⋅d→r
where A is the starting point and B is the ending point.
Let point A be (0,0) and point B be (x0,2x0). The potential at point A is given as V(0,0)=0.
The differential displacement vector d→r can be expressed as:
d→r=dx^i+dy^j
The electric field →E is given as:
→E=E0^i+2E0^j
The dot product →E⋅d→r is:
→E⋅d→r=(E0^i+2E0^j)⋅(dx^i+dy^j)=E0dx+2E0dy
The potential at point B can be calculated as:
V(x0,2x0)=V(0,0)−∫(x0,2x0)(0,0)→E⋅d→r
Since V(0,0)=0, we have:
V(x0,2x0)=−∫x00E0dx−∫2x002E0dy
- For the first integral:
−∫x00E0dx=−E0(x)x00=−E0x0
- For the second integral:
−∫2x002E0dy=−2E0(y)2x00=−2E0(2x0)=−4E0x0
Now, adding both contributions:
V(x0,2x0)=−E0x0−4E0x0=−5E0x0
Thus, the potential at the point (x0,2x0) is:
V(x0,2x0)=−5E0x0
Topper's Solved these Questions
Similar Questions
If unifrom electric filed →E=E0ˆi+2E0ˆj, where E0 is a constant, exists in a region of space and at (0,0) the electric potential V is zero, then the potential at (x0,0) will be.
View SolutionAn electric field E=(20ˆi+30ˆj) N/C exists in the space. If the potential at the origin is taken be zero, find the potential at (2m,2m).
View SolutionThe electric field and the electric potential at a point are E and V respectively.
View SolutionAn electric field E=(20ˆi+30ˆj) N/C exists in the space. If thepotential at the origin is taken be zero, find the potential at (2m,2m).
View SolutionIn a certain region of space the electric potential V is known to be constant. Is the electric field in this region (a) positive (b) zero ,or (c ) negative ?
View SolutionConisder an electric field →E=E0ˆx where E0 is a constant .
The flux through the shaded area (as shown in the figure) due to this field is
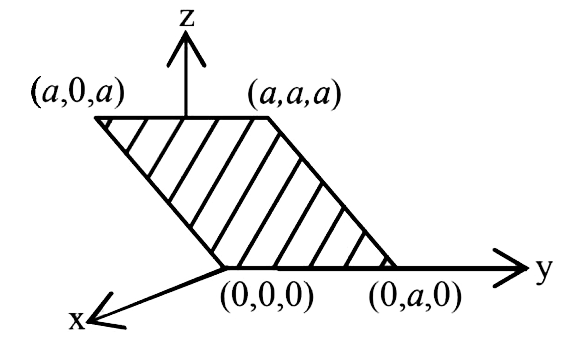 View Solution
View SolutionAn electric field →E=20yˆj exist in space . The potential at (5 m, 5 m) is taken to be zero. The potential at origin is
View SolutionAn electric field →E=Bxˆi exists in space, where B=20V/m2. Taking the potential at (2m, 4m) to be zero, find the potential at the origin.
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in figure. The y−andz−compo≠nts of the electric field are zero in this region. If the electric potential is 10 V at the origin, then the potential at x = 2.0 m is
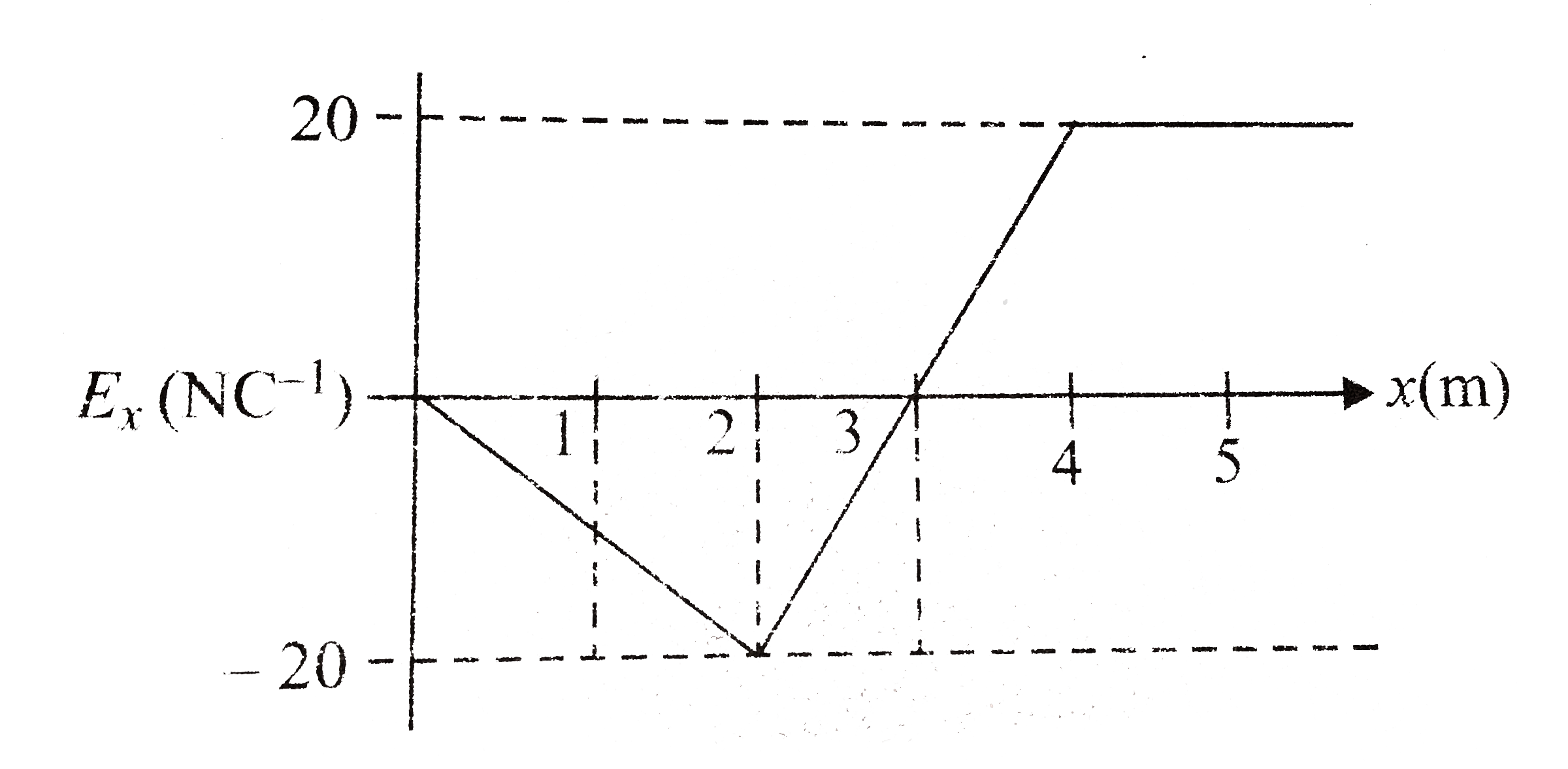 View Solution
View SolutionIn certain region of space with volume 0.2 m3 the electric potential is found to be 5V throughout. The magnitude of electric field is this region is
View Solution

