The figure shows a modified Young’s double slit experimental set-up. Here SS2−SS1=λ/4.
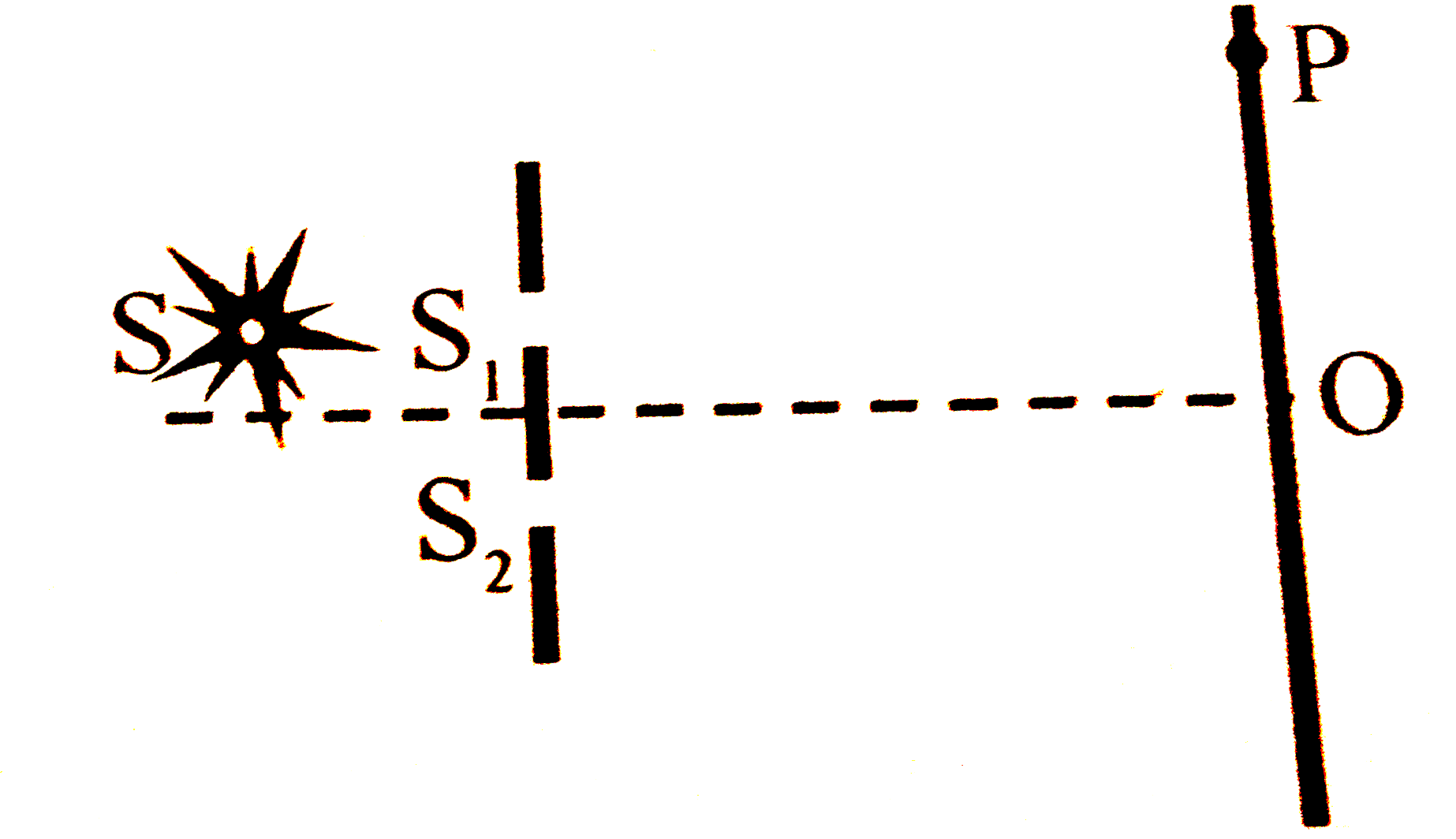
(a) Write the condition for constructive interference.
(b) Obtain an expression for the fringe width.
The path difference S2P−S1P=[yndD+λ4]
For constructive interference , path difference =nλ,
Where n=0,1,2,3,…..
[yndD+λ4]=nλ,
So, position of nth bright fringe is =yn=(n−14)λDd
Fringe widthβ=yn−yn−1
Or β=λDd
Topper's Solved these Questions
Similar Questions
The figure shows a modified Young's double slit experimental set-up.
Here SS2−SS1=λ/4.
(a) Write the condition for constructive interference.
(b) Obtain an expression for the fringe width.
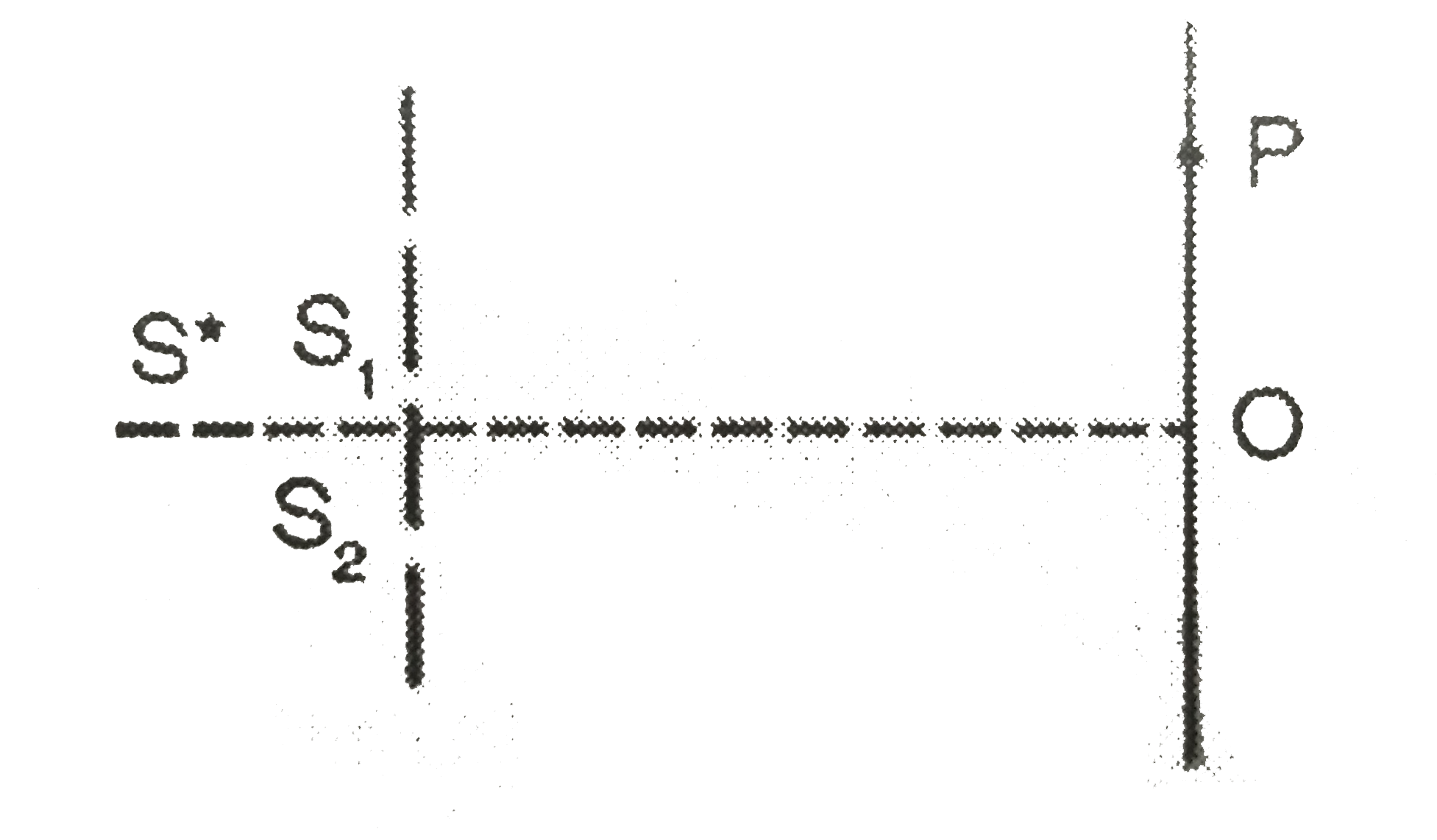
View SolutionThe figure shows a modified Young's double slit experimental set-up.
Here SS2−SS1=λ/4.
(a) Write the condition for constructive interference.
(b) Obtain an expression for the fringe width.
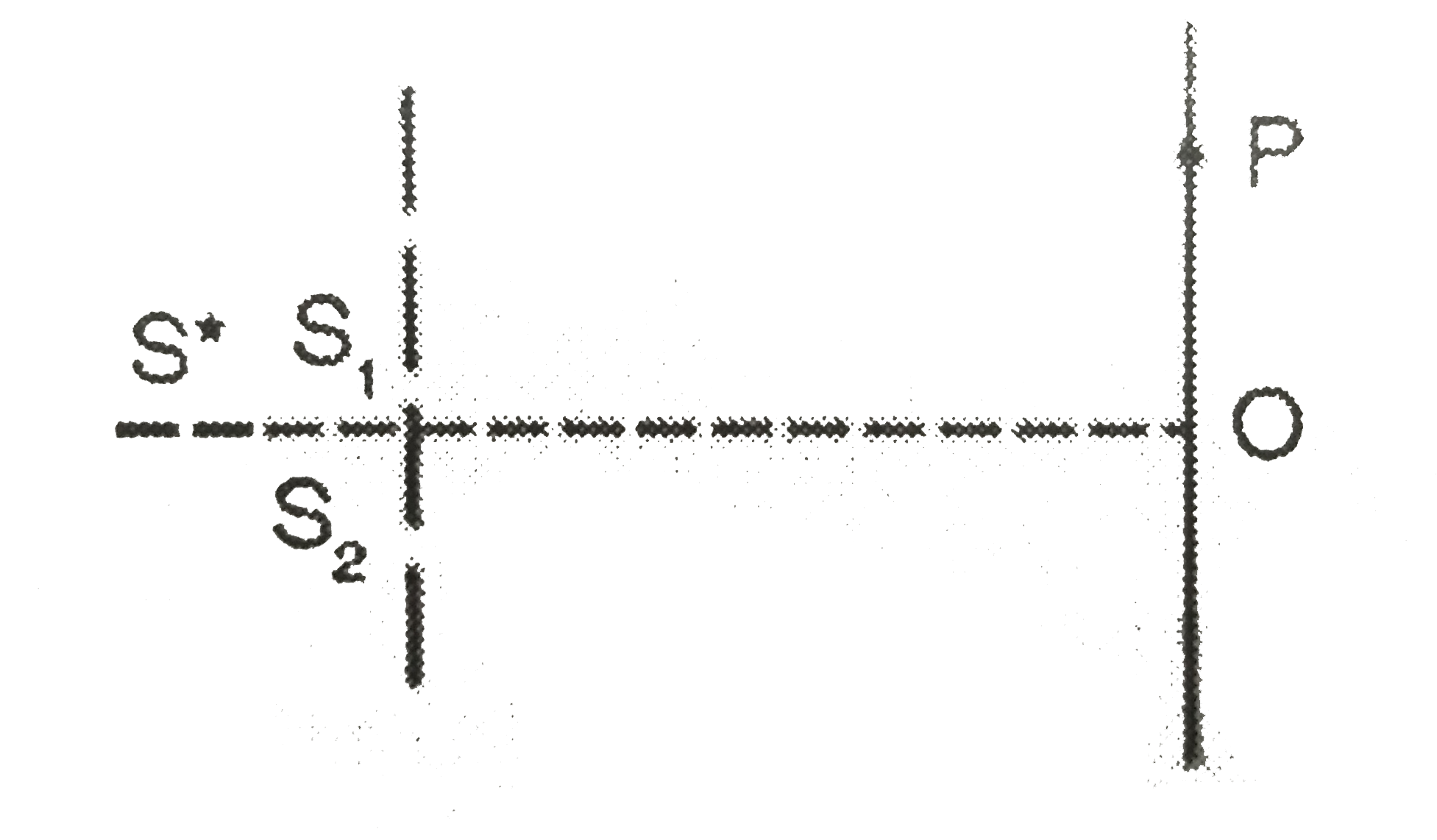
View Solution
Knowledge Check
The fringe width in Young’s double slit experiment increases when
AWavelength increasesBDistance between the slits increasesCDistance between the source and screen decreasesDThe width of the slits increasesIn a Young's double slit experiment, let S1 and S2 be the two slits, and C be the centre of the screen. If ∠S1CS2=θ and λ is the wavelength, the fringe width will be
AλθBλθC2λθDλ2θ
Fig. shows an experimental set up simillar to Young's double slit experiment to observe interference of light. Here SS2−SS1=λ/4. Write down the conditions of (i) Contstructive interference
(ii) Destructive interference at any point P in terms of path diff. (S2P−S1P). Does the central fringe observed in the above set up lie above or below O ? Give reason.
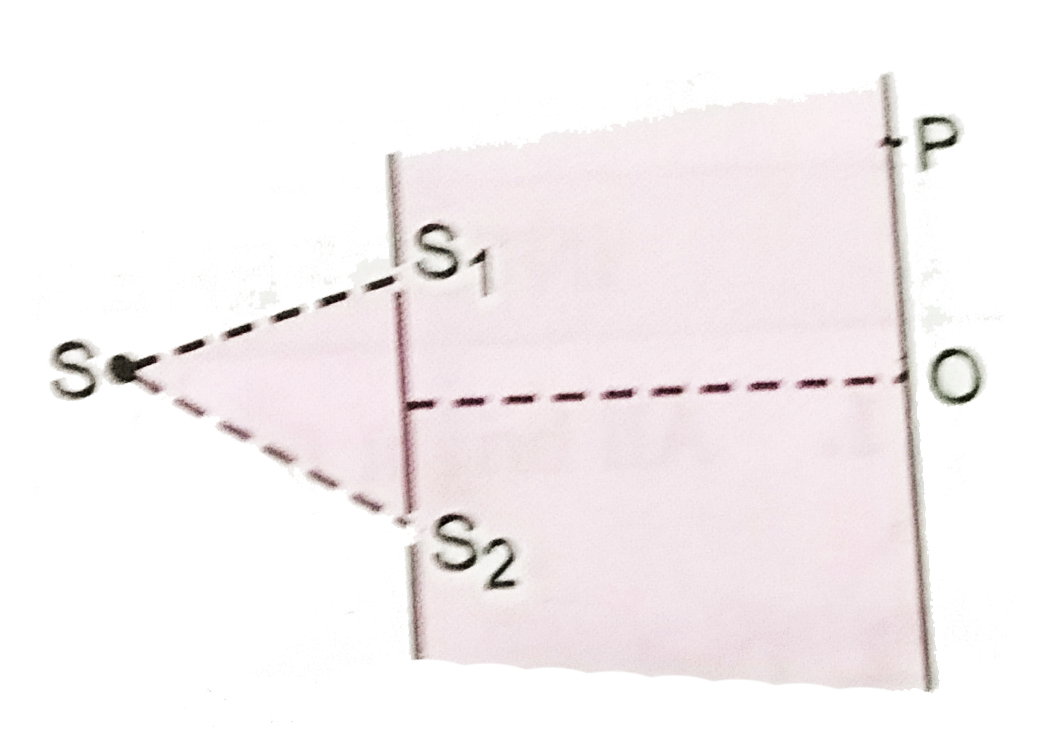
View SolutionState the importance of coherent sources in the phenomenon of interference.
In Young's double-slit experiment to produce interference pattern, obtain the conditions for constructive and destructive interference.
Hence, deduce the expression for the fringe width.
How does the fringe width get affected, if the entire experimental apparatus of Young's is immersed in water ?
View SolutionState the importance of coherent sources in the phenomenon of interference. In Young's double slit expet-ment to produce interference pattern obtain the conditions for constructive and destructive interference. Hence deduce the expression for the fringe width. How does the firinge width get affected, if the entire experimental apparatus of Young's is immersed in water ?
View SolutionState the importance of coherent sources in the phenomenon of interference. In Young's double slit expet-ment to produce interference pattern obtain the conditions for constructive and destructive interference. Hence deduce the expression for the fringe width. How does the firinge width get affected, if the entire experimental apparatus of Young's is immersed in water ?
View SolutionIn a modified set up of Young's double slit experiment, it is given that SS2−SS1=λ4 i.e., the source S is not equidistant from the slits S1andS2.
(a) Obtain the condition for constructive and destructive interference at any point P on the screen in terms of the path difference Δ=S2P−S1P.
(b) Does the observed central bright fringe lie above or below O ? Give reason in support of your answer.
View SolutionIf the width of the slit S in Young's double slit experiment is gradually increased

View Solution
