In a modified set up of Young's double slit experiment, it is given that SS2−SS1=λ4 i.e., the source S is not equidistant from the slits S1andS2.
(a) Obtain the condition for constructive and destructive interference at any point P on the screen in terms of the path difference Δ=S2P−S1P.
(b) Does the observed central bright fringe lie above or below O ? Give reason in support of your answer.
(a) The Net path difference between two waves, reaching on the screen through two slits, is given as:
SS2P−SS1P=(SS2−SS1)+(S2P−S1P)
It is given that SS2−SS1=λ4 and we know that (S2P−S1P)=Δ=xdD, where .d. is the separation between slits S1andS2and.D. the distance of screen from the double-slit.
∴ Net path difference =λ4+xdD

(i) For constructive interference λ4+xdD=nλ, where n=0,1,2,3...
⇒xdD=nλ−λ4=(4n−1)λ4⇒(xn)bright=(4n−1)λD4d
(ii) For destructive interference λ4+xdD=(2n−1)λ2, where n=1,2,3, . .
⇒xdD=(4n−3)λ4⇒(xn)dark=(4n−3)λD4d.
(b) For central bright fringe n=0 and hence (x0)bright=−λD4d. Thus, the observed central bright fringe shifts towards the line of slit S2.
Topper's Solved these Questions
- WAVE OPTICSBOOK - U-LIKE SERIESCHAPTER - WAVE OPTICSEXERCISE - LONG ANSWER QUESTIONS-II
12 Videos
- WAVE OPTICSBOOK - U-LIKE SERIESCHAPTER - WAVE OPTICSEXERCISE - SELF ASSESSMENT TEST SECTION A (MULTIPLE CHOICE QUESTIONS)
6 Videos
- WAVE OPTICSBOOK - U-LIKE SERIESCHAPTER - WAVE OPTICSEXERCISE - SHORT ANSWER QUESTIONS
29 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - U-LIKE SERIESCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - SECTION B
1 Videos
Similar Questions
Fig. shows an experimental set up simillar to Young's double slit experiment to observe interference of light. Here SS2−SS1=λ/4. Write down the conditions of (i) Contstructive interference
(ii) Destructive interference at any point P in terms of path diff. (S2P−S1P). Does the central fringe observed in the above set up lie above or below O ? Give reason.
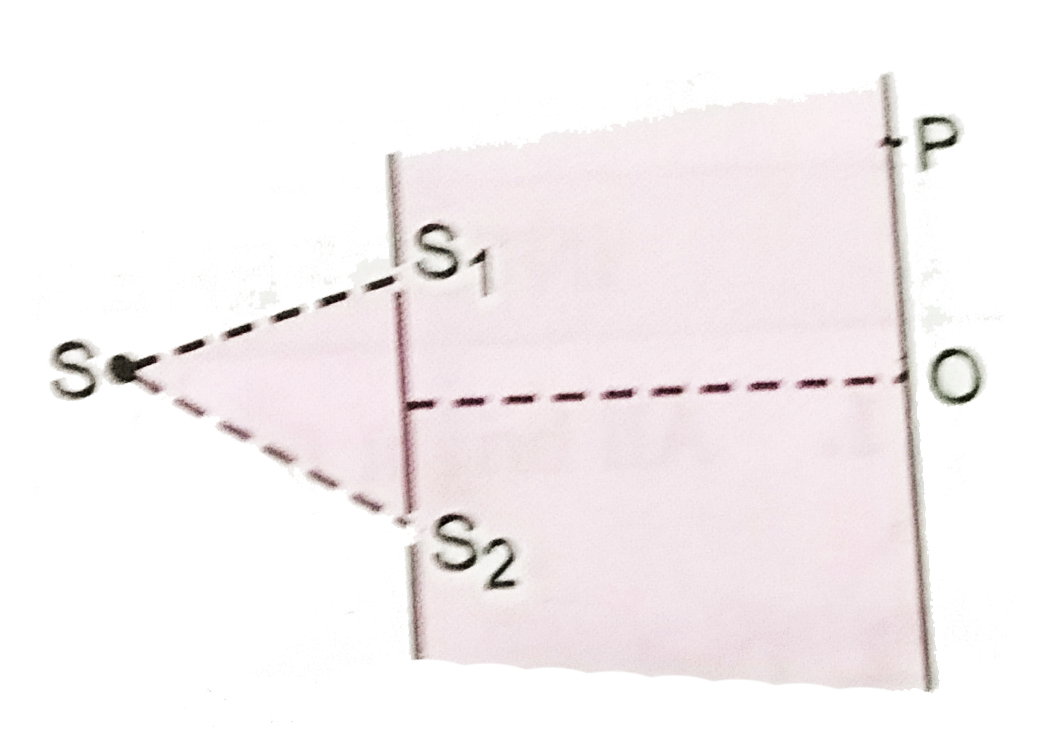
View SolutionThe figure shows a modified Young’s double slit experimental set-up. Here SS2−SS1=λ/4.
(a) Write the condition for constructive interference.
(b) Obtain an expression for the fringe width.
View Solution
Knowledge Check
In the case of light waves from two coherent sources S1 and S2, there will be constructive interference at an arbitrary point P, the path difference S1P−S2P is
A(n+12)λBnλC(n−12)λDλ2In the case of light waves from two coherent sources S1 and S2, there will be constructive interference at an arbitrary point P, the path difference S1P−S2P is
A(n+12)λBnλC(n−12)λDλ2In Young’s double slit experiment, the central bright fringe can be identified
ABy using white light instead of monochromatic lightBAs it is narrower than other bright fringesCAs it is wider than other bright fringesDAs it has a greater intensity than the other bright fringes
In a modified YDSE, sources S is kept in front of slit S1. Find the phase difference at point O that is equidistant from slits S1 and S2 and point P that is in front of slit S1 in the following situations.
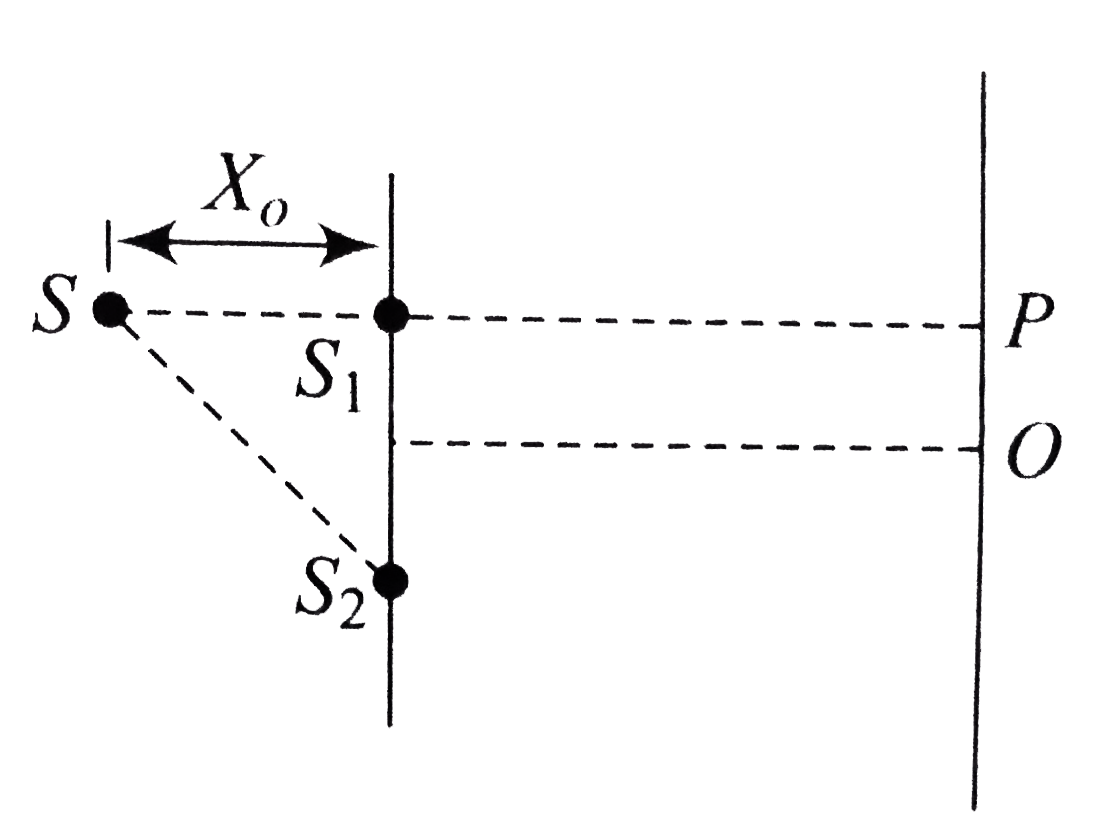
A liquid of refractive index μ is filled between the screen and slits.
View SolutionIn a Young's double-slit experiment, let S1 and S2 be the two slits, and C be the centre of the screen. If ∠S1CS2=θ and λ is wavelength, the fringe width will be
View SolutionIn a modified Young's double-slit experiment, source S is kept in front of slit S1 as shown in the following figure. Find the phase difference at a point that is equidistant from slits S1 and S2 and point P that is in front of slit S1 in the following situations:

If a liquid is filled between the slit and the source S, what is the phase difference?
View SolutionIn a Young's double slit experiment, let S1 and S2 be the two slits, and C be the centre of the screen. If ∠S1CS2=θ and λ is the wavelength, the fringe width will be
View SolutionIn a Young's double slit experiment, let S1 and S2 be the two slits, and C be the centre of the screen. If ∠S1CS2=θ and λ is the wavelength, the fringe width will be
View Solution
