find minimum value of F such that $m_{2}$ starts its motion on the ground

$\frac{μ_{0} (2 m_{1} + m_{2}) g}{2}$

$μ_{0} (2 m_{1} + m_{2}) g$

$μ_{0} (m_{1} + m_{2}) g$

$\frac{μ_{0} (m_{1} + m_{2}) g}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$F x - μ_{0} m_{1} g x - \frac{1}{2} k x^{2} = 0$
$x = \frac{μ_{0} m_{2} g}{k}$

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

The coefficient of friction between block $A$ of mass $m_{1} = 5 k g$ and block $B$ of mass $m_{2} = 10 k g$ is $μ_{2} = 0.5$ . There is no friction froce between block $B$ and fixed horizontal surface. A force of $300 N$ acts on block $B$ in horizontal direction and a horizontal force of magnitude $F$ acts on block $A$ as shown , both towards right. Initially there is no relative motion between the blocks. The minimum value of $F$ such that relative motion starts between $A$ and $B$ is $:$

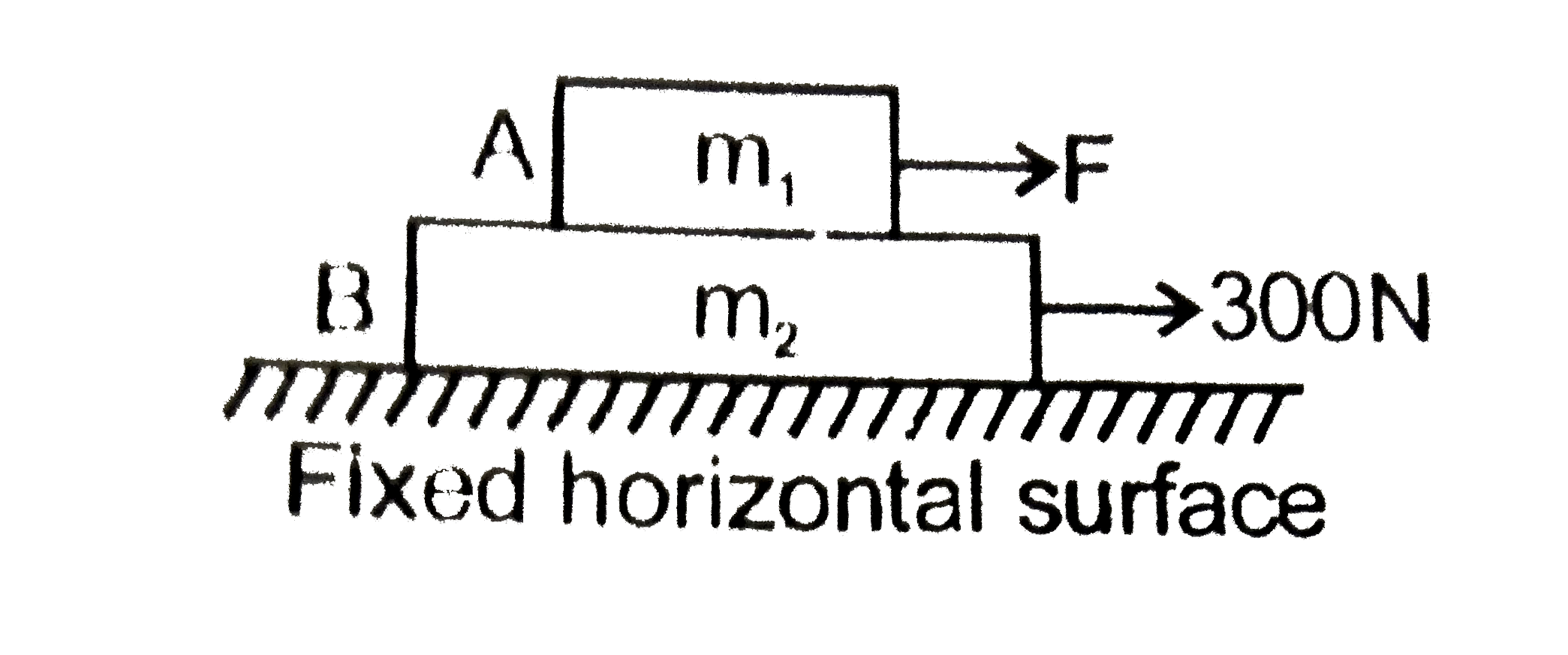View Solution
When force F applied on $m_{1}$ and there is no friction between $m_{1}$ and surface and the coefficient of friction between $m_{1} and m_{2}$ is $μ .$ What should be the minimum value of F so that there is on relative motion between $m_{1} and m_{2}$

View Solution
A small block of mass $m$ is projected on a larger block of mass $10 m$ and length $l$ with a velocity $v$ as shown in the figure. The coefficient of friction between the two block is $μ_{2}$ while that between the lower block and the ground is $μ_{1}$ . Given that $μ_{2} > 11 μ_{1}$ .

(a) Find the minimum value of $v$ , such that the mass $m$ falls off the block of mass $10 m$ .
(b) If $v$ has minimum value, find the time taken by block $m$ to do so.
View Solution
In the figure the minimum value of $a$ at which the cylinder starts rising up the inclined surface is

View Solution
If the system shown in the figure is rotated in a horizontal circle with angular velocity $ω$ . Find $(g = 10 m / s^{2})$
(a) the minimum value of $ω$ to start relative motion between the two blocks.
(b) tension in the string connecting $m_{1}$ and $m_{2}$ when slipping just starts between the blocks
The coefficient of frition between the two masses is $0.5$ and there is no friction between $m_{2}$ and ground. The dimensions of the masses can be neglected. (Take $R = 0.5 m, m_{1} = 2 K g, m_{2} = 1 K g)$

View Solution
Initially, both the blocks are at rest on horizontal surface as shown in the figure. Find the minimum value of force F in (N) so that sliding starts between the blocks $(g = 10 m s^{- 2})$

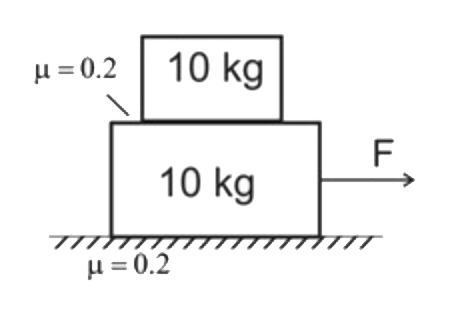View Solution
In Fig. initialy the system is at rest .Find out minimum value of $F$ for which sliding start between the two blocks Given $m_{A} = 10 k g$ and $m_{B} = 20 k g$
View Solution
A spring-mass system ( $m_{1}$ + massless spring + $m_{2}$ ) fall freely from a height $h$ before $m_{2}$ colliding inelastically with the ground. Find the minimum value of $h$ so that block $m_{2}$ will break off the surface. Assume k=stiffness of the spring.

View Solution
A ball of mass 1 kg is dropped from 20 m height on ground and it rebounds to height 5m. Find magnitude of change in momentum during its collision with the ground. (Take $g = 10 m / s^{2}$ )
View Solution
Minimum value of of f $(x) = 2 x^{2} - 4 x + 5 i s$
View Solution

find minimum value of F such that m2 starts its motion on the ground

The correct Answer is:A

Fx−μ0m1gx−12kx2=0 x=μ0m2gk

Similar Questions

Recommended Questions

find minimum value of F such that $m_{2}$ starts its motion on the ground

$F x - μ_{0} m_{1} g x - \frac{1}{2} k x^{2} = 0$
$x = \frac{μ_{0} m_{2} g}{k}$