In the figure the minimum value of a at which the cylinder starts rising up the inclined surface is

gtanθ
gcotθ
gsinθ
gcosθ
The correct Answer is:A
On the cylinder
If N= normal reation between ylinder and inclinder plane
Nsinθ= horizontal component of N
=ma …(i) Ncosθ= vertical component of N
=mg …(ii)
Driving eq.(i) by (ii) we get,
tanθ=ag
a=gtanθ
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Objective Question
32 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason
28 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
The minimum value of acceleration of wedge for which the block start sliding on the wedge, is:
View Solutionfind minimum value of F such that m2 starts its motion on the ground

View Solution
A uniform cylinder of mass M and radius R is released from rest on a rough inclined surface of inclination θ with the horizontal as shown in figure. As the cylinder rolls down the inclined surface, the maximum elongation it the spring stiffness k is
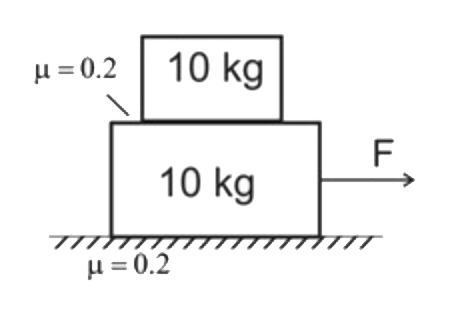
View SolutionInitially, both the blocks are at rest on horizontal surface as shown in the figure. Find the minimum value of force F in (N) so that sliding starts between the blocks (g=10ms−2)
View SolutionA box of mass 8kg placed on a rough inclined plane of inclination θ its downward motion can be prevented by applying an upward pull F and it can be made to slide upward appliying a force 2F .The coefficient of friction between the box and the inclined plane is
View SolutionConsider the situation in which one end of a massless spring of spring constant k is connected to a cylinder of mass m and the other to a rigid support. When cylinder is given a gentle push in horizontal direction it starts oscillating on the rough horizontal surface. During the oscillation cylinder rolls without slipping. When calculated, motion of cylinder is found to be S.H.M. with time period T=2π√3m2K and equation of SHM is x=Asinωt, where symbols have their usual meaning.

:
Q The minimum value of coefficient of friction such that the cylinder does not slip on the surface is:
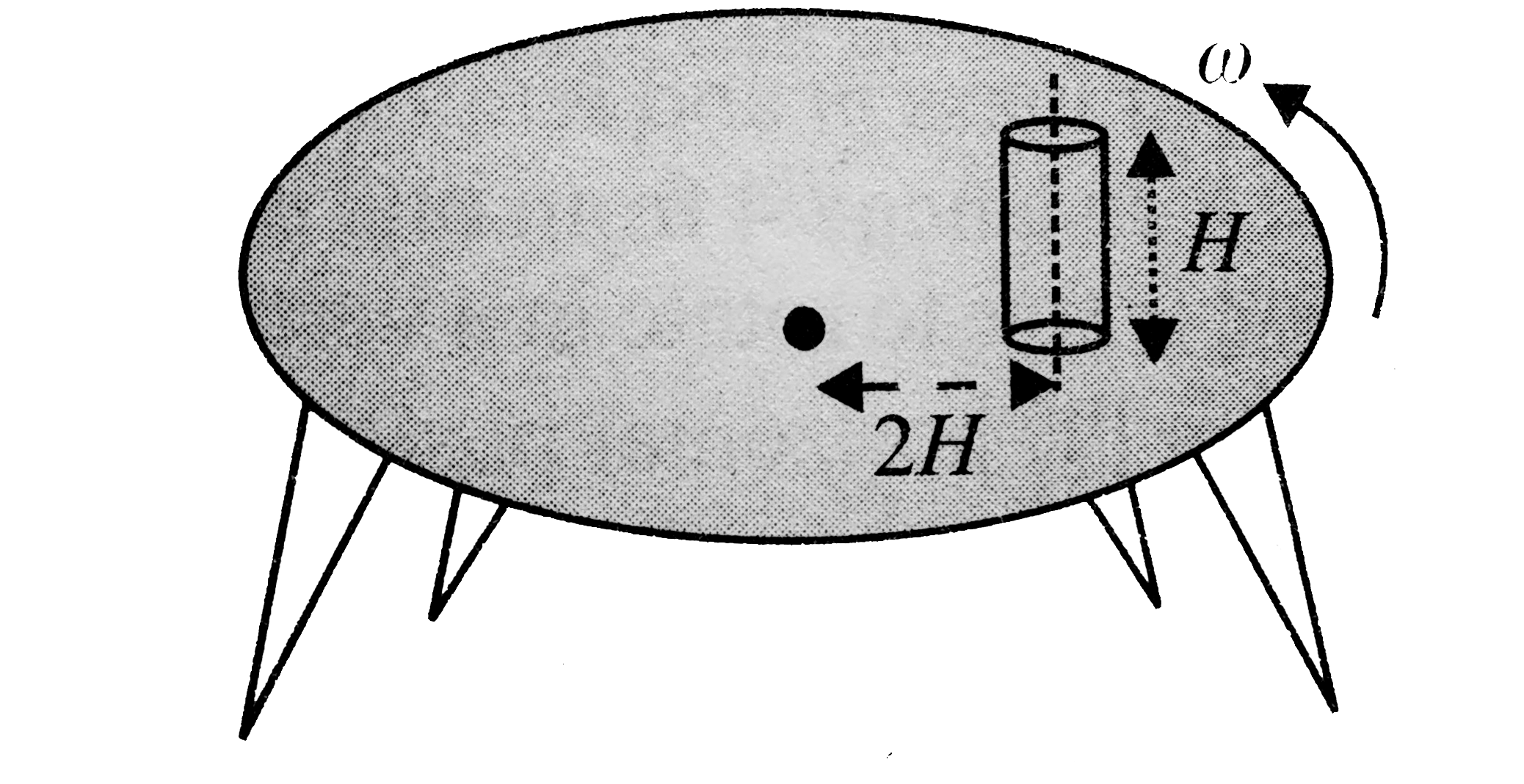
View SolutionA cylinder of height H and diameter H/4 is kept on a frictional turntable as shown in Fig. The axis of the cylinder is perpendicular to the surface of the table and the distance of axis of the cylinder is 2H from the centre of the table. The angular speed of the turntable at which the cylinder will start toppling (assume that friction is sufficient to prevent slipping) is
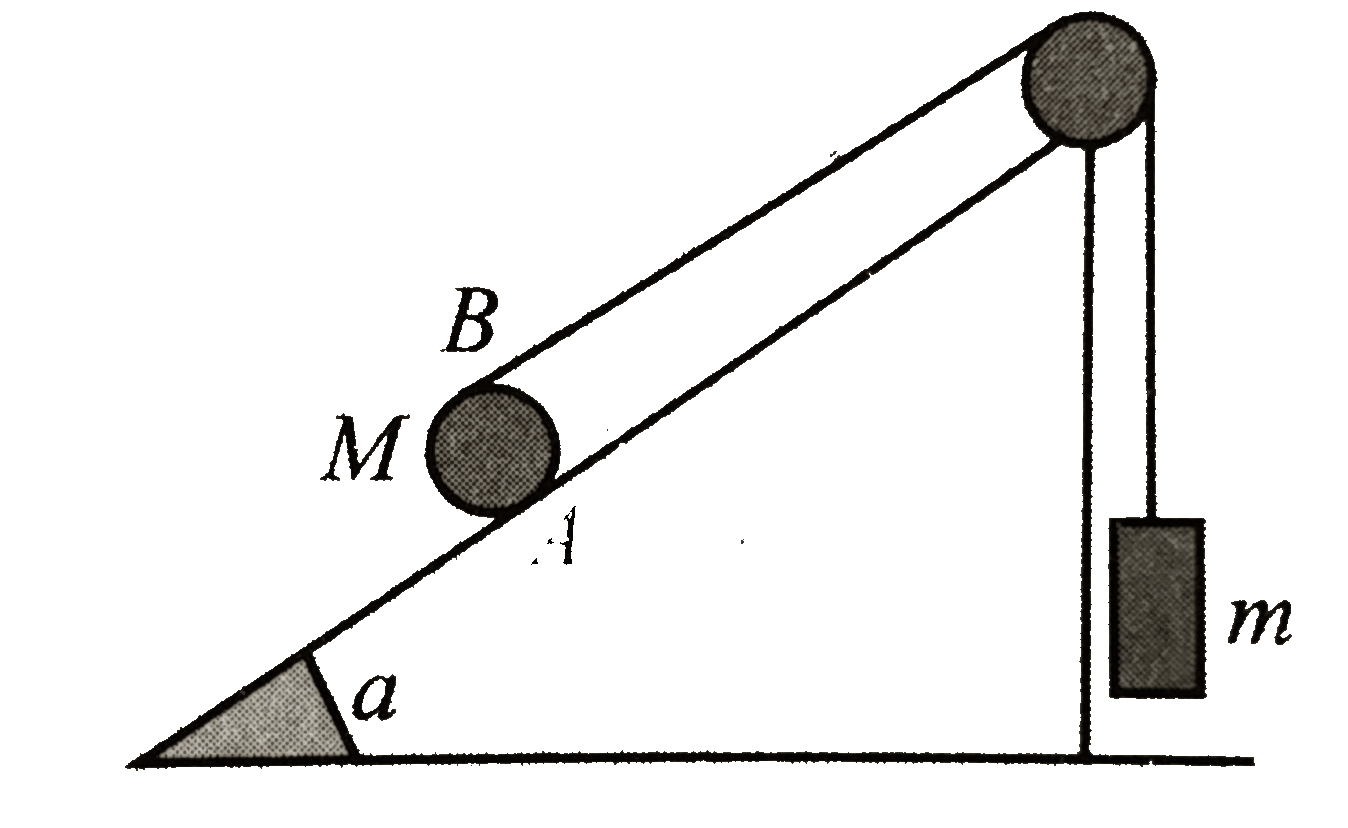
View SolutionFind the tension in the tape and the linear acceleration of the cylinder up the incline, assuming there is no slipping. (TakeM=4m and g=10m/s2)
View SolutionA horizontal uniform rod of mass 'm' has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass 'm' which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.
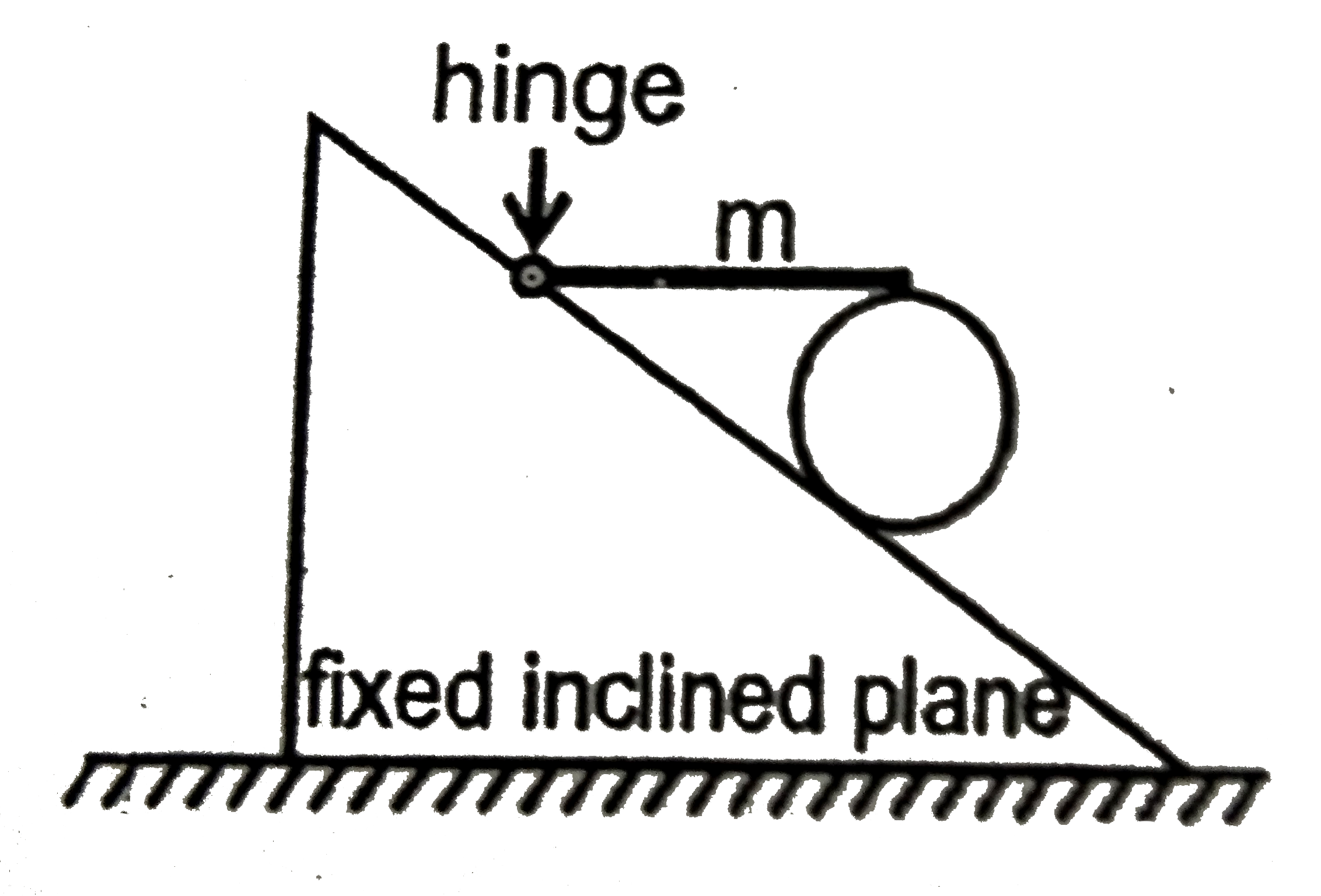
The ratio of magnitude of frictional force on the cylinder due to the rod and the magnitude of frictional force on the cylinder due to the inclined plane is :
View SolutionA container shown in Fig. is accelerated horizontally with acceleration a.
a. Find the minimum value of a at which liquid just starts spilling out.

View Solution
