A pendulum of length 1m hangs from an inclined wall. Suppose that this pendulum is released at an initial angle of 10∘ and it bounces off the wall elastically when it reaches an angle of −5∘ as shown in the figure. Take g=π2m/s2. The period of this pendulum is (in second)

2/3
3/2
3/4
4/3
The correct Answer is:D
We take θ=(10∘)cos(πt), calculate t when θ=−5∘. This gives t=2/3(s). The period is 2 times this.
Similar Questions
Find the length of seconds pendulum at a place where g=π2m/s2.
View SolutionA partile is projected up an incline (inclination angle =30∘) with 15√3m/s at an angle of 30∘ with the incline (as shown in figure) (g=10m/s2)
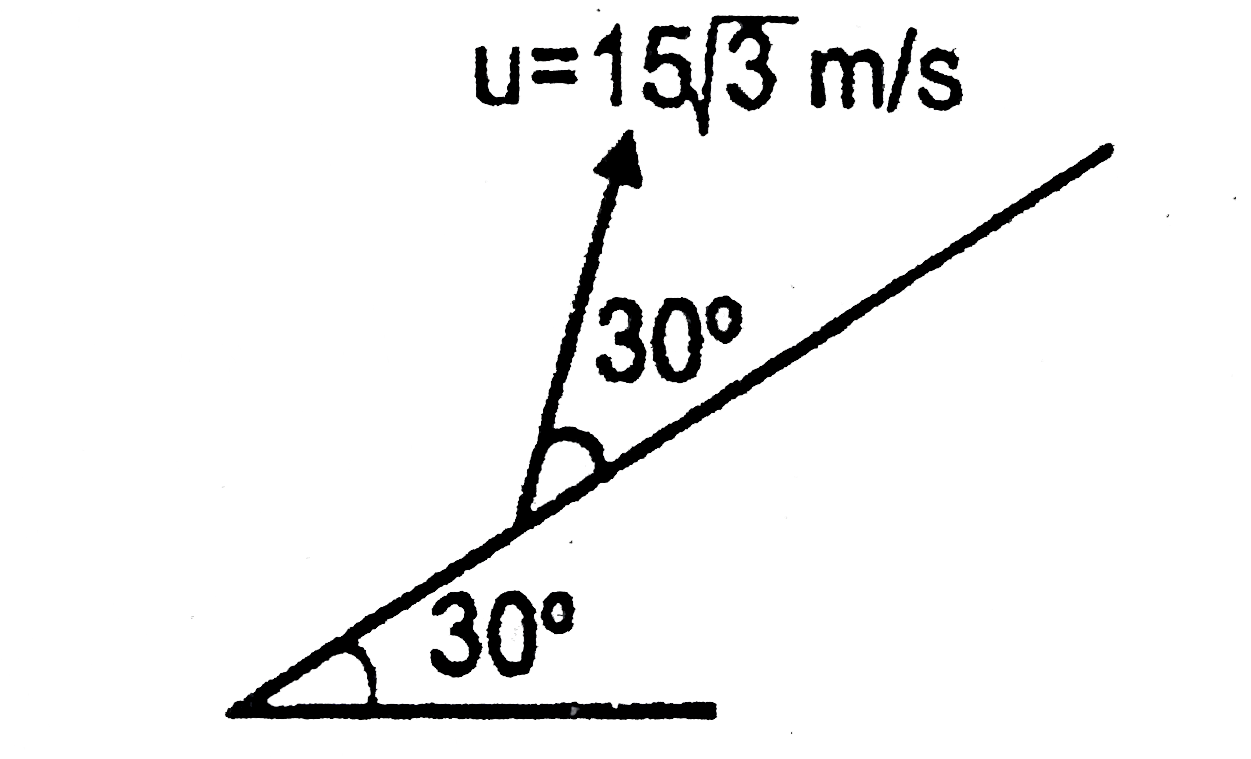 View Solution
View SolutionFind the length of seconds pendulum at a place where g=4π2m/s2.
View SolutionA simple pendulum is released from A as shown. If m and 1 represent the mass of the bob and length of the pendulum, the gain kinetic energy at B is
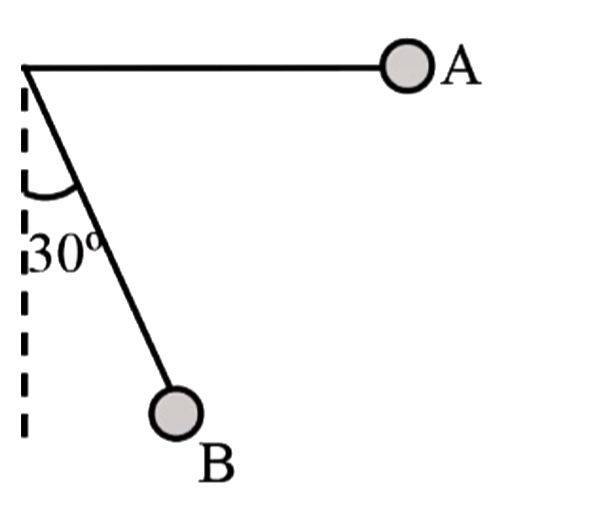 View Solution
View SolutionA pendulum bob has a speed of 3ms−1 at its lowest position. The pendulum is 0.5 m long. The speed of the bob, when string makes an angle of 60∘ to the vertical is (take, g=10ms−1)
View SolutionA simple pendulum of length 1m is attached to the ceiling of an elevator which is accelerating upward at the rate of 1m/s2. Its frequency is approximately :-
View SolutionA pendulum bob has a speed 3m/s while passing through its lowest position. What is its speed when it makes an angle of 600 with the vertical? The length of the pendulum is 0.5m Take g=10ms2.
View SolutionA simple pendulum of length 5 m is suspended from the ceiling of a cart. Cart is sliding down on a frictionless surface having angle of inclination 60°. The time period of the pendulum is
View SolutionA simple pendulum is suspended from the ceiling of a car taking a turn of radius 10 m at a speed of 36 km/h. Find the angle made by the string of the pendulum with the vertical if this angle does not change during the turn. Take g=10ms2.
View SolutionA pendulum consists of a small mass m at the end of a string of length L. The pendulum is pulled aside making an angle θ with the vertical and released. Taking the suspension point as the axis, at the instant of release
View Solution

