A partile is projected up an incline (inclination angle =30∘) with 15√3m/s at an angle of 30∘ with the incline (as shown in figure) (g=10m/s2)
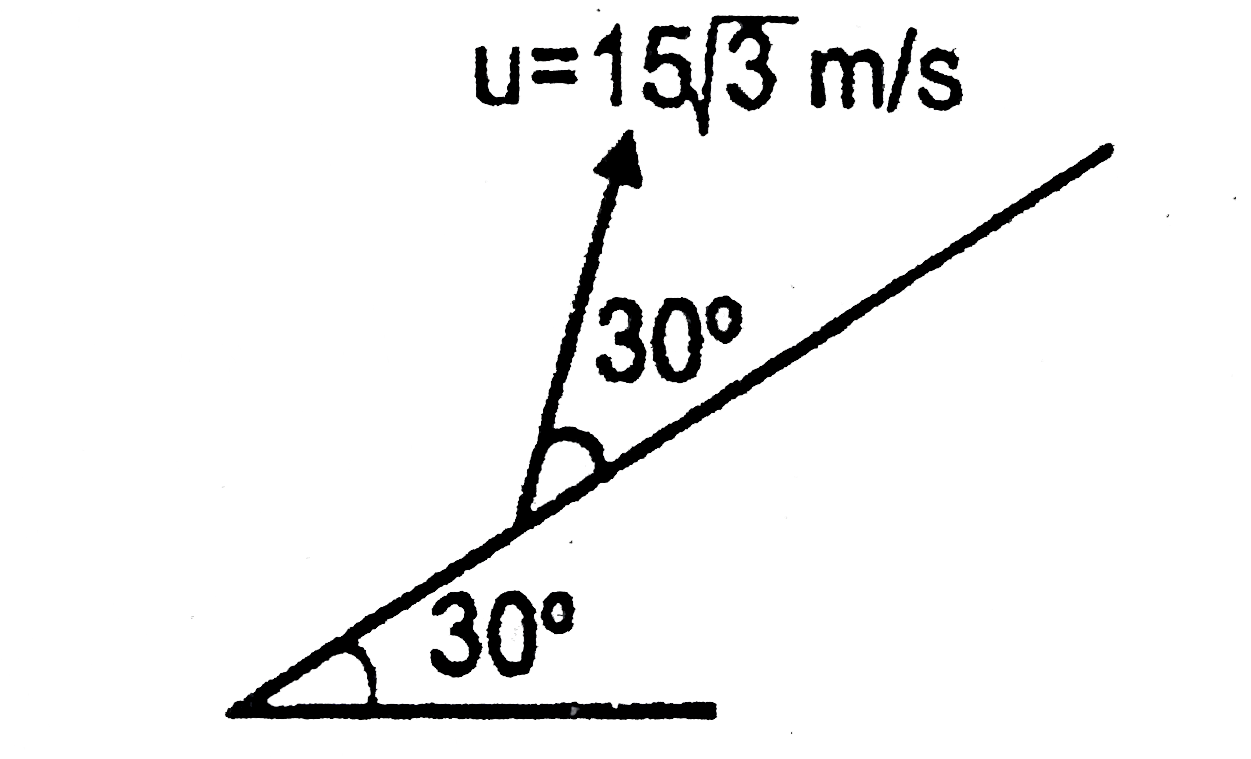
1.5 sec later, angle between acceleration & velocity is 120∘
1.5 sec later, angle between acceleration & velocity is 60∘.
Range on the incline is 45m
Time of flight on the incline is 3 sec.
The correct Answer is:A, C, D
For motion ⊥ to incline 0=(usin30∘)t−12(gcos30∘)lt2
⇒t=2usin30∘gcos30∘=3sec= Time of flight
⇒ at 1.5sec, velocity is parallel to incline
⇒ angle between velocity & acceleration is 120∘

for motion parallel to incline
R=(ucos30∘)t−12(gsin30∘)t2 & t=3sec
⇒R=45m
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS106videos
TEST PAPERS
- BOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS784videos
TEST PAPERS
- BOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS784videos
TEST PAPERS
- BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems13videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS130videos
TEST SERIES
Similar Questions
A ball is projected from the bottom of an inclined plane of inclination 30∘, with a velocity of 30ms−1, at an angle of 30∘ with the inclined plane. If g=10ms−2 , then the range of the ball on given inclined plane is
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)
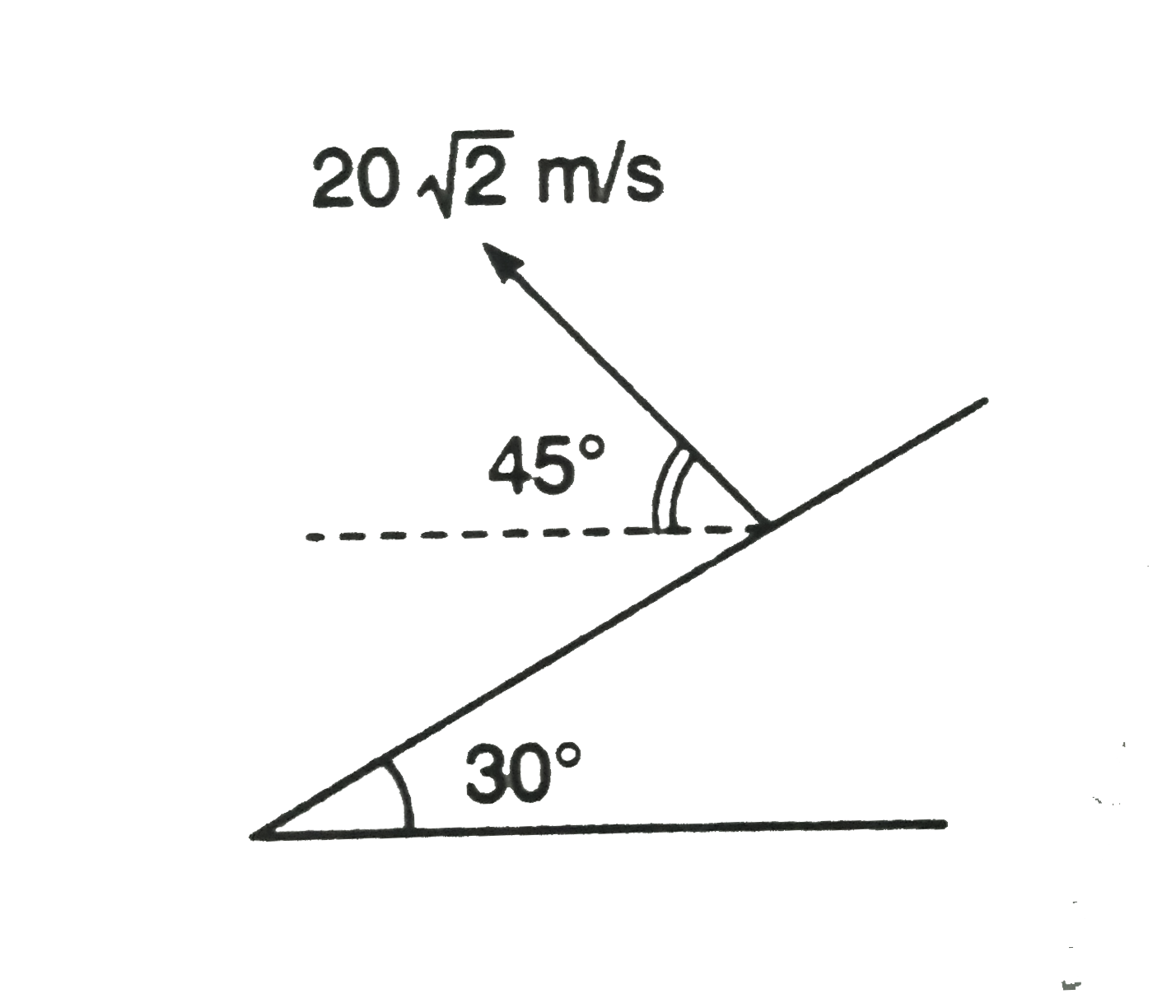 View Solution
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)
 View Solution
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)
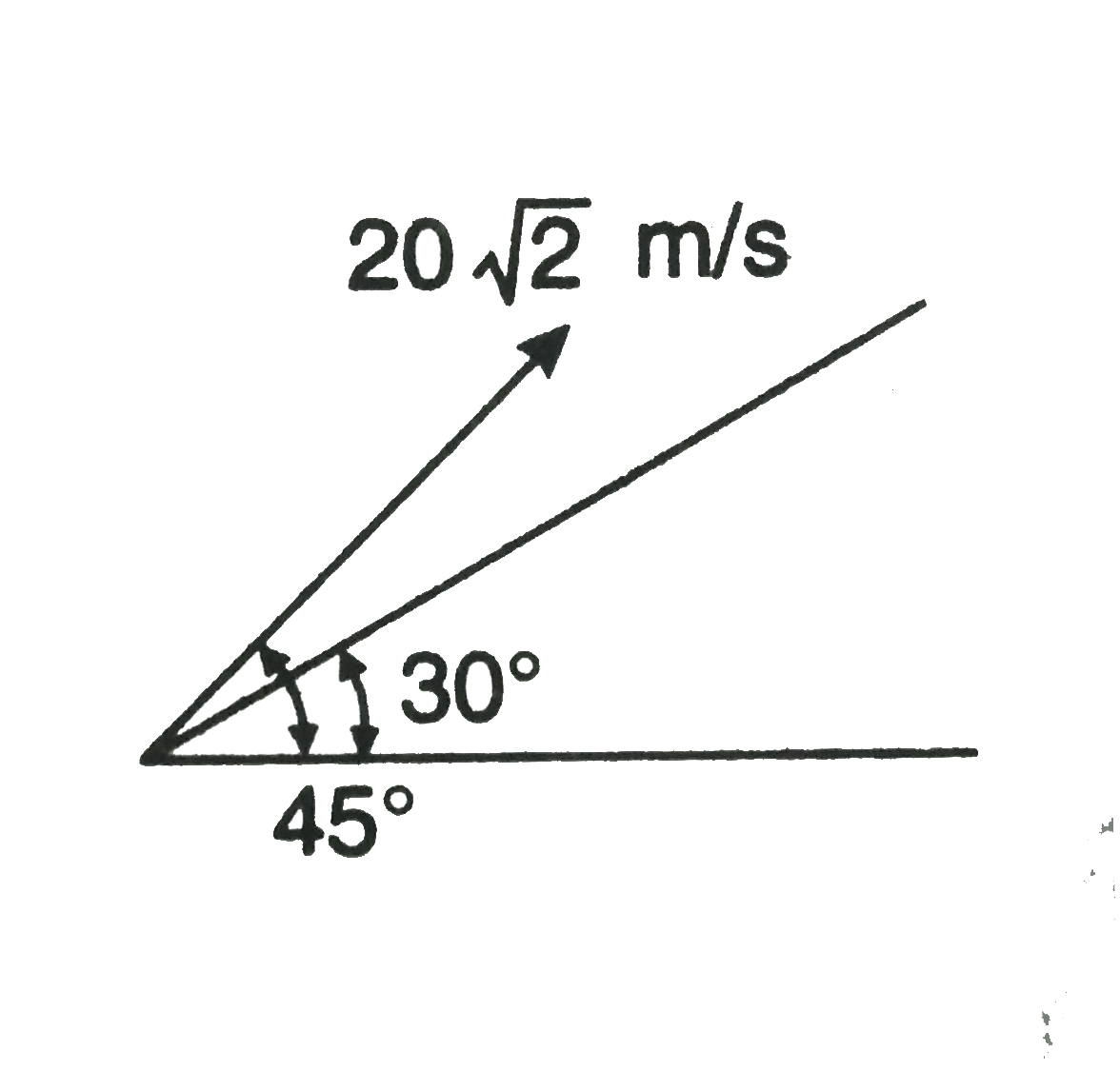 View Solution
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘ with velocity of 40m/s at an angle of 60∘ with horizontal. Find the speed of the particle when its velocity vector is parallel to the plane. Take g=10m/s2.
View SolutionA particle is prjected up an inclined with initial speed v=20m/s at an angle θ=30∘ with the plane. The component of its velocity perpendicular to the plane when it strikes the plane is:
View SolutionA particle is projected up an inclined plane with initial speed 20 m/s at an angle 30∘ with the plane. Find the component of its velocity (in m/s) perpendicular to the plane, when it strikes the plane.
View SolutionA cylinder rolls down on an inclined plane of inclination 37∘ from rest. Coefficient of friction between plane and cylinder is 0.5. Calculate the time ( in s) of travelling down the incline 8 m as shown in figure .(g=10m/s2)
 View Solution
View SolutionA projectile is projected upward with speed 2m/s on an incline plane of inclination 30∘ at an angle of 15∘ from the plane. Then the distance along the plane where projectile will fall is :
View SolutionA projectile is projected upward with speed 2m/s on an incline plane of inclination 30∘ at an angle of 15∘ from the plane. Then the distance along the plane where projectile will fall is :
View Solution

