Question

The Earth has a circular orbit of radius r and period t around the sum, Mars has a circular orbit of radius R and period T. In order to send a spacecraft from the Earth to Mars, it is convenient to launch the spacecraft inot an elliptical orbit whose perihelion coincides with the orbit of the Earth and whose aphelion coincides with the orbit of Mars, this orbit requires the least amount of energy for a trip to Mars. The time t' taken by a spacecraft to reach Mars from the Earth satisfies:

Options

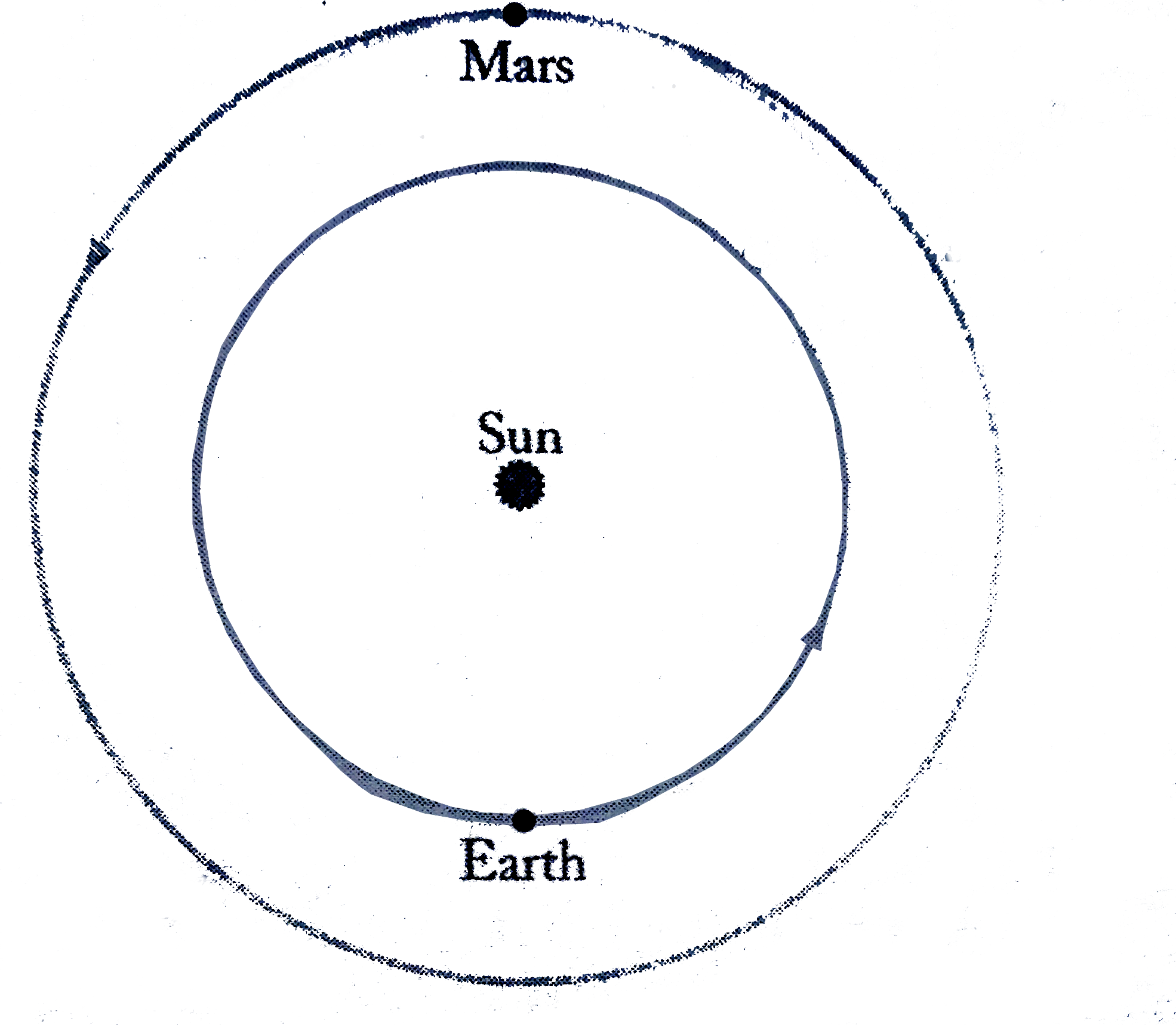
A. `t' = (t + T)//2`
B. `t'^(2) = (t^(2) + T^(2))//2`
C. `t'^(2//3) = (t^(2//3) + T^(2//3))//2`
D. `(2t)^(2//3) = (t^(2///3) + T^(2//3))//2`

Answer

D

Explanation

Use Kepler's Law of Periods