If L is the angular momentum of a satellite revolving around earth is a circular orbit of radius r with speed v , then
L∝v
L∝r
L∝√r
L∝√v
The correct Answer is:C
To solve the problem of finding the angular momentum L of a satellite revolving around the Earth in a circular orbit of radius r with speed v, we can follow these steps:
Step 1: Understand the definition of angular momentum
The angular momentum L of an object moving in a circular path is given by the formula:
L=r×p
where p is the linear momentum of the object, and r is the radius of the circular path.
Step 2: Express linear momentum
The linear momentum p of the satellite can be expressed as:
p=mv
where m is the mass of the satellite and v is its speed.
Step 3: Substitute linear momentum into the angular momentum formula
Substituting the expression for linear momentum into the angular momentum formula, we have:
L=r×mv=mvr
Step 4: Find the expression for speed v
For a satellite in a circular orbit, the gravitational force provides the necessary centripetal force. The gravitational force acting on the satellite is given by:
F=GMmr2
where G is the gravitational constant and M is the mass of the Earth. The centripetal force required to keep the satellite in circular motion is:
F=mv2r
Setting these two forces equal gives:
GMmr2=mv2r
Step 5: Simplify the equation
We can cancel m from both sides (assuming m≠0):
GMr2=v2r
Multiplying both sides by r:
GMr=v2
Taking the square root of both sides gives:
v=√GMr
Step 6: Substitute v back into the angular momentum equation
Now we substitute v back into the angular momentum equation:
L=mvr=m(√GMr)r
This simplifies to:
L=m√GM√r
Step 7: Conclusion
From the final expression, we can conclude that the angular momentum L is directly proportional to the square root of the radius r:
L∝√r
The angular momentum L of an object moving in a circular path is given by the formula:
L=r×p
where p is the linear momentum of the object, and r is the radius of the circular path.
The linear momentum p of the satellite can be expressed as:
p=mv
where m is the mass of the satellite and v is its speed.
Substituting the expression for linear momentum into the angular momentum formula, we have:
L=r×mv=mvr
For a satellite in a circular orbit, the gravitational force provides the necessary centripetal force. The gravitational force acting on the satellite is given by:
F=GMmr2
where G is the gravitational constant and M is the mass of the Earth. The centripetal force required to keep the satellite in circular motion is:
F=mv2r
Setting these two forces equal gives:
GMmr2=mv2r
We can cancel m from both sides (assuming m≠0):
GMr2=v2r
Multiplying both sides by r:
GMr=v2
Taking the square root of both sides gives:
v=√GMr
Now we substitute v back into the angular momentum equation:
L=mvr=m(√GMr)r
This simplifies to:
L=m√GM√r
From the final expression, we can conclude that the angular momentum L is directly proportional to the square root of the radius r:
L∝√r
Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - C (PREVIOUS YEARS QUESTIONS)
51 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - A (OBJECTIVE TYPE QUESTIONS)
41 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
Knowledge Check
A satellite is orbiting the earth in a circular orbit of radius r. Its
AKnetic enegy varies as rBangular momentum varies as 1√rClinear momentum varies as 1rDfrequency of revolution varies as 1r3/2An earth satellite is moving around the earth in circular orbit. IN such case what is conserved
AvelocityBlinear momentumCangular momentumDnone of the above
Find the angular momentum of a satellite of mass m moving round the earth of mass m if its orbital radius is r, assuming it to be circular. Express it in terms of G, M, m and r, where G is the universal gravitational constant ?
View SolutionThe orbital speed of a satellite revolving around a planet in a circular orbit is v0 . If its speed is increased by 10 % ,then
View SolutionA small satellite of mass m is revolving around earth in a circular orbit of radius r0 with speed v0 . At certain point of its orbit, the direction of motion of satellite is suddenly changed by angle θ=cos−1(3/5) by turning its velocity vector , such that speed remains constant. The satellite consequently goes to elliptical orbit around earth. the ratio of speed at perigee to speed at apogee is
View SolutionTwo satellites revolve around the ‘Sun’ as shown in the figure. First satellite revolves in a circular orbit of radius R with speed v1 . Second satellite revolves in elliptical orbit, for which minimum and maximum distance from the sun are R3 and 5R3 respectively. Velocities at these positions are v2 and v3 respectively. The correct order of speeds is
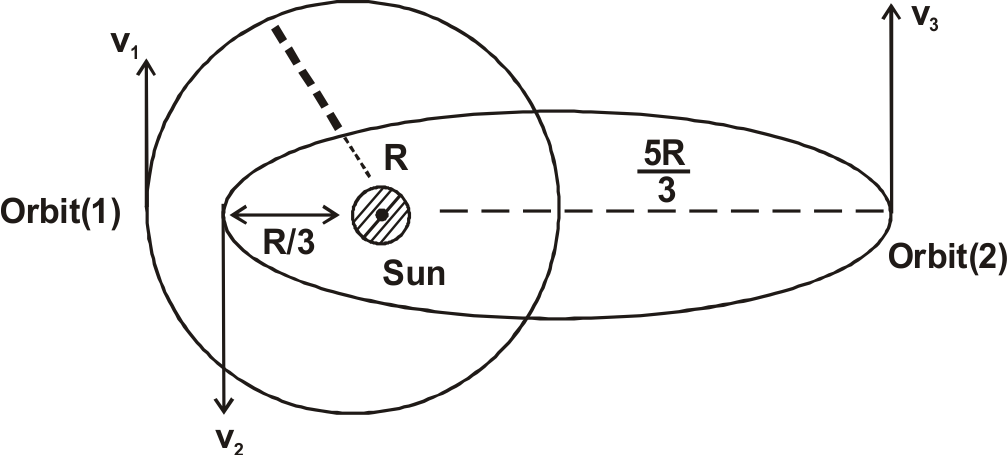
View SolutionA satellite is revolving around the earth. Ratio of its orbital speed and escape speed will be.
View SolutionThe orbital angular momentum of a satellite revolving at a distance r from the centre is L . If the distance is increased to 16 r, then the new angular momentum will be
View Solution