A uniform solid sphere of mass m and radius 'R' is imparted an initial velocity v0 and angular ω0=2v0R and then placed on a rough inclined plane of inclination 'theta' and coefficient of friction μ=2tanθ as shown. The time after which the sphere will start rolling without slipping is

v02gsinθ
v04gsinθ
v06gsinθ
v08gsinθ
The correct Answer is:C
N=mgcosθ
fk=μN=2tanθtmgcosθ=2mgsinθ
fk−mgsinθ=ma
2mgsinθ−mgsinθ=ma
∴a=gsinθ
Now, τcm=Icmα
fkR=25mR2α
2mgsinθ=25mRα
α=5gsinθR
Where the rolling without slipping starts
v=ωR
v0+at=(ω0−αt)R
v0+gsinθt=ω0R−5gsinθt
v0+6gsinθt=2v0
∴=v06gsinθ
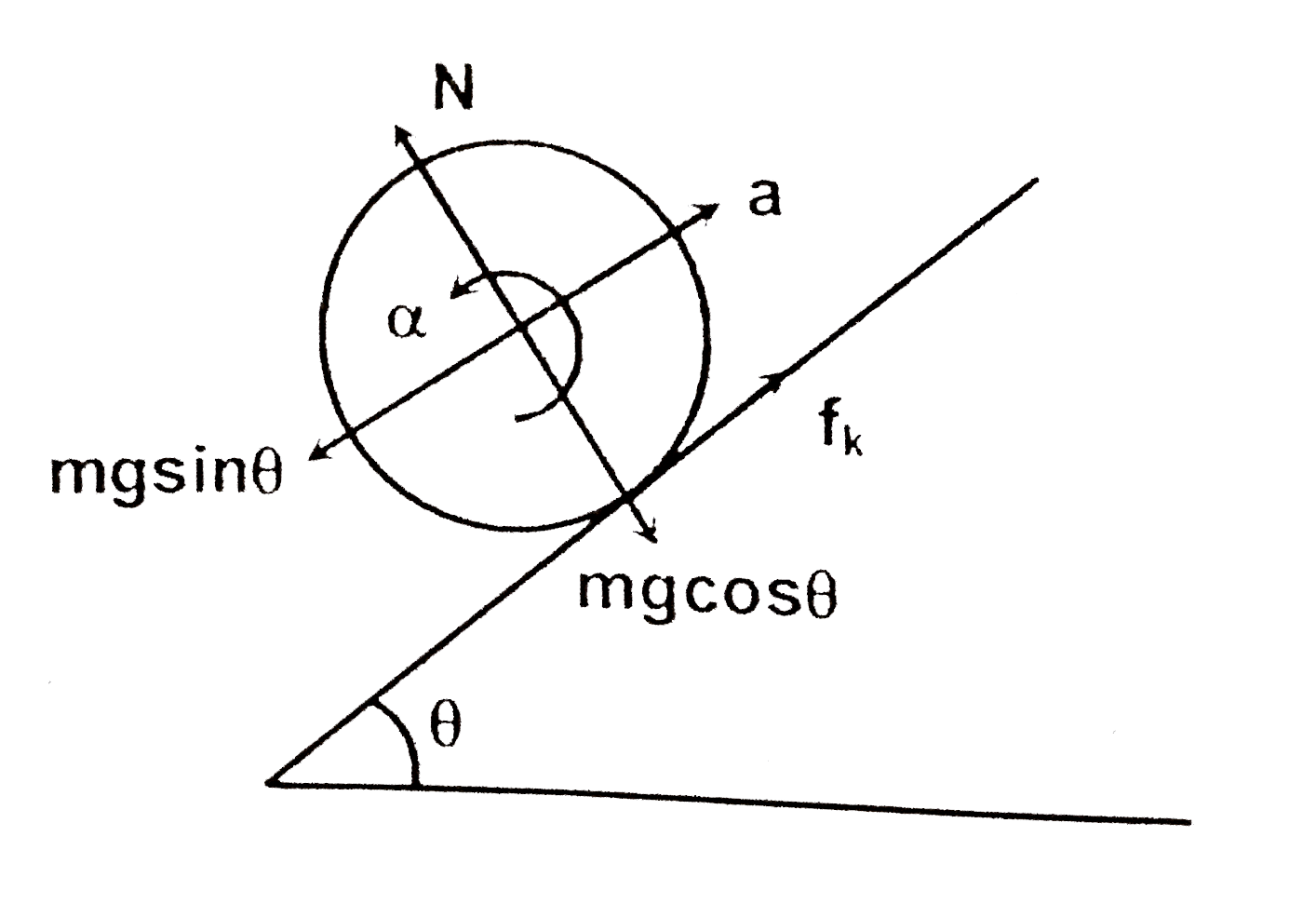
Similar Questions
A sphere of mass M rolls without slipping on the inclined plane of inclination θ. What should be the minimum coefficient of friction, so that the sphere rolls down without slipping ?
View SolutionA hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
View SolutionA cylinder of mass m radius R is spined to a clockwise angular velocity ωo and then gently placed on an inclined plane for which coefficient of friction μ=tanθ,θ is the angle of inclined plane with the horizontal. The centre of mass of cylinder will remain stationary for time

View SolutionIf a solid cylinder rolls without slipping on an inclined plane of inclination '0' then the minimum coefficient of friction required to support pure rolling is
View SolutionA solid cylinder of mass 3kg is placed on a rough inclined plane of inclination 30∘. If g=10ms2, then the minimum frictional force required for it to roll without slipping down the plane is

View SolutionA solid cylinder is rolling without slipping on a plane having inclination θ and the coefficient of static friction μs. The relation between θ and μs is
View SolutionA block of mass m attached with a an ideal spring of force constant k is placed on a rough inclined plane having inclination θ with the horizontal and coefficient of friction μ=1/2tanθ, Initially the block is held stationary with the spring in its relaxed state, find the maximum extension in the spring if the block is released.

View SolutionA uniform solid sphere of radius R, rolling without sliding on a horizontal surface with an angular velocity ω0, meets a rough inclined plane of inclination θ=60∘. The sphere starts pure rolling up the plane with an angular velocity ω Find the value of ω.

View Solution
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View SolutionA solid sphere of radius R is set into motion on a rough horizontal surface with a inear speed v0 in forward direction and an angular with a linear speed v0 in forward directioin and an angular velocity ω0=v0/2R in counter clockwise direction as shown in figure. If coefficient of friction μ then find
a. the time after which sphere starts pure rolling,
b. the linear speed of sphere when it starts rolling and
c. the work down by friction over a long time.
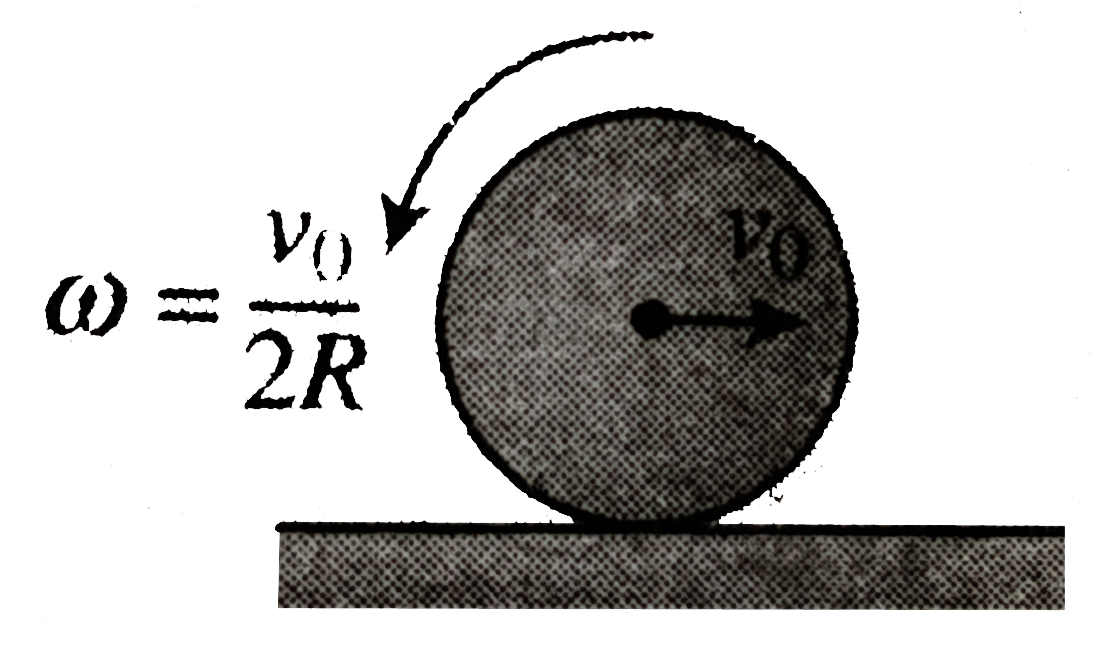
View Solution
