A cylinder of mass m radius R is spined to a clockwise angular velocity and then gently placed on an inclined plane for which coefficient of friction is the angle of inclined plane with the horizontal. The centre of mass of cylinder will remain stationary for time

The correct Answer is:D
Step by step video & image solution for A cylinder of mass m radius R is spined to a clockwise angular velocity omega_(o) and then gently placed on an inclined plane for which coefficient of friction mu = tan theta, theta is the angle of inclined plane with the horizontal. The centre of mass of cylinder will remain stationary for time by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.65
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.66
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.63
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
A mass placed on an inclined place is just in equilibrium. If μ is coefficient of friction of the surface, then maximum inclination of the plane with the horizontal is
View SolutionA block with a square base measuring a×a and height h, is placed on an inclined plane. The coefficient of friction is μ. The angle of inclination (θ) of the plane is gradually increased. The block will
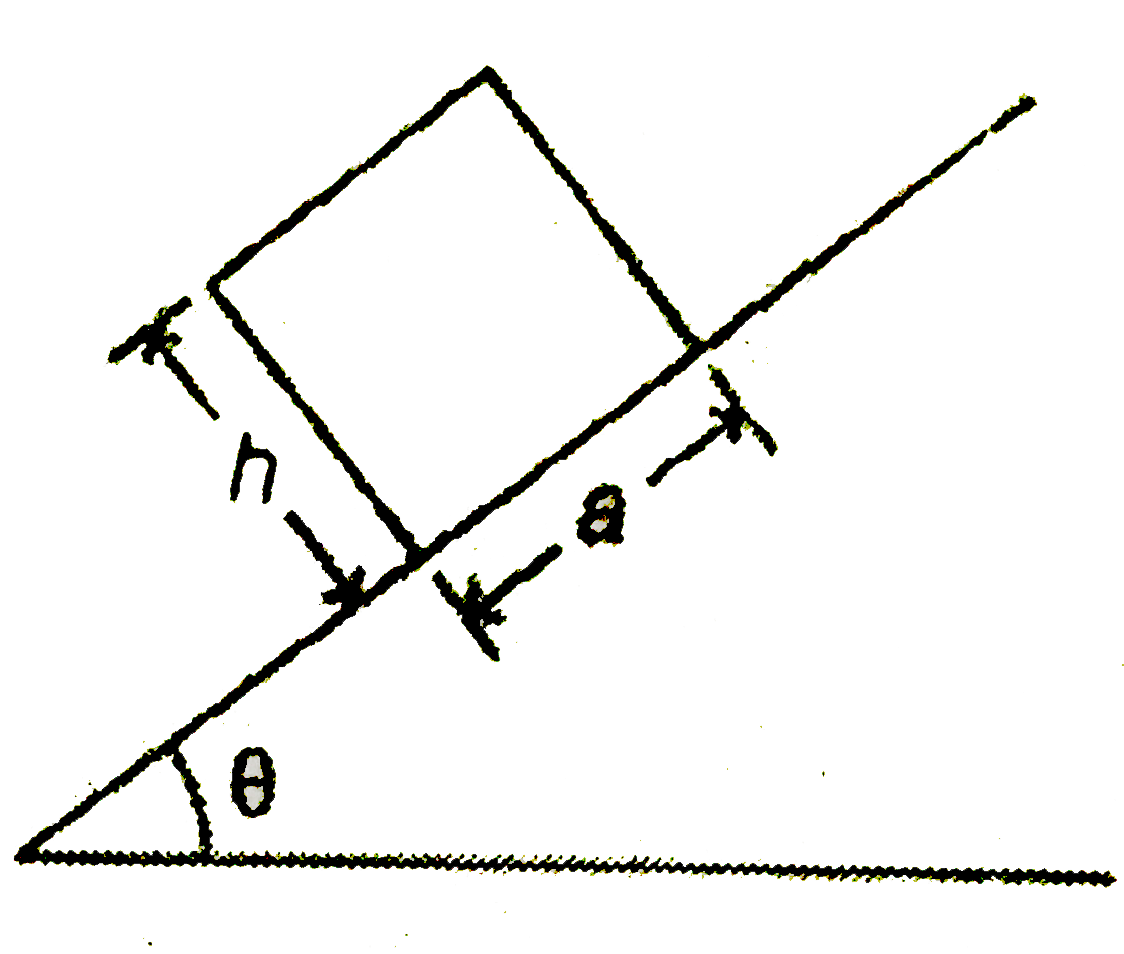
View Solution
Knowledge Check
A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
Aθ=tan−1μBθ=cos−1μCθ=sin−1μDθ=sec−1μA block of mass m is at rest on an inclined plane. The coefficient of static friction is μ. The maximum angle of incline before the block begins to slide down is :
Atan−1(μ/m)Btan−1(μ)Ctan−1(μ/2)Dcos−1(μ)
A uniform solid sphere of mass m and radius 'R' is imparted an initial velocity v0 and angular ω0=2v0R and then placed on a rough inclined plane of inclination 'theta' and coefficient of friction μ=2tanθ as shown. The time after which the sphere will start rolling without slipping is

View SolutionA sphere of radius R is projected with a reverse spin ω0 down a rough inclined plane with a speed v0 for which coefficient of friction is μ>tanθ, where θ is angle of the inclination. Show that it will turn back if
ω>5v0μ2R(μ−tanθ)

View SolutionA uniform circular cylinder of mass m and radius r is given an initial angular velocity ω and no initial translational velocity it is placed in contact with a plane inclined at an angle α to the horizontal. If there is a coefficient of friction μ for sliding between the cylinder and plane. Find the distance the cylinder moves up before sliding stops also calculate the maximum distance it travels up the plane assume μ>tanα.
View SolutionA body of mass m is placed on a rough surface with coefficient of friction μ inclined at θ. If the mass is in equilibrium , then
View SolutionA body of mass m is placed on a rough surface with coefficient of friction μ inclined at θ. If the mass is in equilibrium , then
View SolutionA cylinder of mass M and radius R rolls on an inclined plane. The gain in kinetic energy is
View Solution
