Two circles of unequal radii have four common tangents. A transverse common tangent meets the direct common tangents at the points P & Q. If length of direct tangent (between the point of contacts) is 8 then length of PQ is
The correct Answer is:8
To solve the problem, we need to find the length of the segment PQ formed by the intersection of the transverse common tangent and the direct common tangents of two circles with unequal radii.
1. Understanding the Geometry:
- We have two circles with unequal radii that have four common tangents: two direct tangents and two transverse tangents.
- The direct common tangents touch the circles at points A and B, and the transverse common tangents meet the direct common tangents at points P and Q.
2. Given Information:
- The length of the direct tangent AB (between the points of contact) is given as 8.
3. Setting Up the Problem:
- Let PA=a and PB=b where P is the point on the direct tangent line.
- Since AB=8, we can express the lengths in terms of a and b:
PA+PB=8⟹a+b=8
4. Finding Lengths:
- The length of segment PQ can be expressed as:
PQ=PA+PB=a+b
- Since a+b=8, we substitute:
PQ=8
5. Conclusion:
- Therefore, the length of PQ is 8.
Final Answer:
The length of PQ is 8.
- We have two circles with unequal radii that have four common tangents: two direct tangents and two transverse tangents.
- The direct common tangents touch the circles at points A and B, and the transverse common tangents meet the direct common tangents at points P and Q.
- The length of the direct tangent AB (between the points of contact) is given as 8.
- Let PA=a and PB=b where P is the point on the direct tangent line.
- Since AB=8, we can express the lengths in terms of a and b:
PA+PB=8⟹a+b=8
- The length of segment PQ can be expressed as:
PQ=PA+PB=a+b
- Since a+b=8, we substitute:
PQ=8
- Therefore, the length of PQ is 8.
The length of PQ is 8.
Similar Questions
Knowledge Check
Two circles with radii 25 cm and 9 cm touch each other externally. Find the length of the direct common tangent.
A32 cmB50 cmC40 cmD30 cm
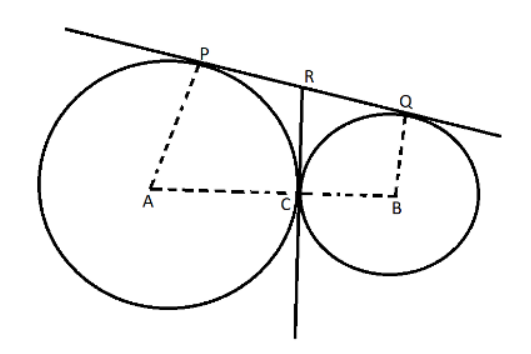
In the figure, two circles touch each other at the point C.Prove that the common tangents to the circles at C, bisect the common tangents at P and Q.
View SolutionProve that the tangent at any point of circle is perpendicular to the radius through the point of contact.
View SolutionProve that the tangent at any point of circle is perpendicular to the radius through the point of contact.
View SolutionIf the length of direct common tangent and transverse common tangent of two circles with integral radii are 3 units and 1 unit respectively, then the reciprocal of the square of the distance between the centres of the circles is equal to
View SolutionTwo equal parabolas have the same vertex and their axes are at right angles. The length of the common tangent to them, is
View SolutionTwo circles of radii r1 and r2,r1>r2≥2 touch each other externally. If θ be the angle between the direct common tangents, then,
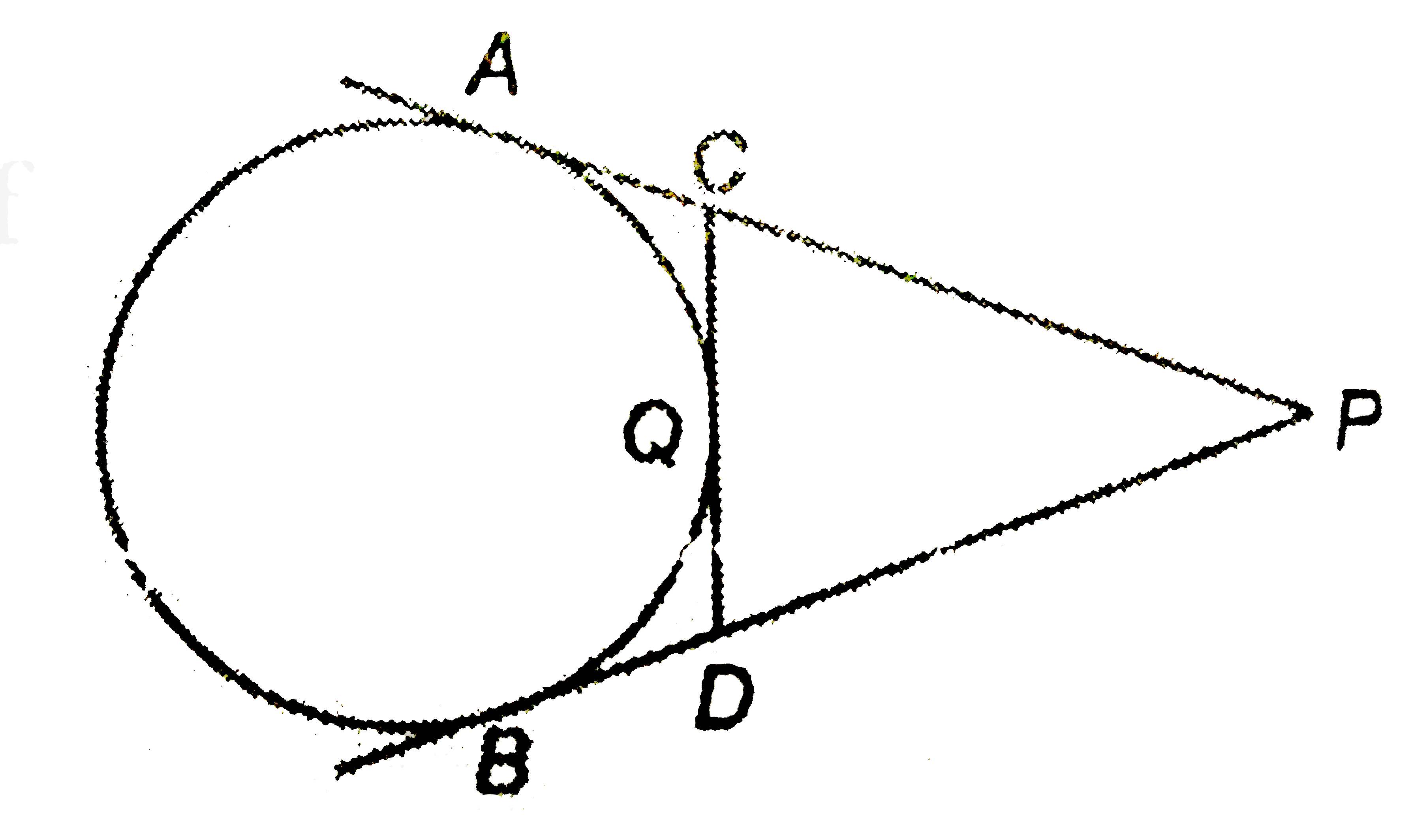
View SolutionIn the given figure PA and PB are tangents to the circle drawn from an external point P. CD is a third tangent touching the circle at Q. If PB=10cm and CQ=2cm. What is the length of PC?
View Solution
