If the length of direct common tangent and transverse common tangent of two circles with integral radii are 3 units and 1 unit respectively, then the reciprocal of the square of the distance between the centres of the circles is equal to
The correct Answer is:0.1
To solve the problem, we need to find the reciprocal of the square of the distance between the centers of two circles given the lengths of their direct and transverse common tangents.
1. Understanding the Given Information:
- Let the radii of the two circles be R1 and R2.
- The length of the direct common tangent is given as 3 units.
- The length of the transverse common tangent is given as 1 unit.
2. Using the Formulas for Tangents:
- The formula for the length of the direct common tangent Ld is:
Ld=√d2−(R1−R2)2
- The formula for the length of the transverse common tangent Lt is:
Lt=√d2−(R1+R2)2
- Here, d is the distance between the centers of the circles.
3. Setting Up the Equations:
- From the direct common tangent:
√d2−(R1−R2)2=3
Squaring both sides:
d2−(R1−R2)2=9(Equation 1)
- From the transverse common tangent:
√d2−(R1+R2)2=1
Squaring both sides:
d2−(R1+R2)2=1(Equation 2)
4. Subtracting the Two Equations:
- Subtract Equation 2 from Equation 1:
(d2−(R1−R2)2)−(d2−(R1+R2)2)=9−1
- This simplifies to:
(R1+R2)2−(R1−R2)2=8
5. Expanding the Squares:
- Expanding both squares:
(R21+2R1R2+R22)−(R21−2R1R2+R22)=8
- Simplifying gives:
4R1R2=8
- Thus:
R1R2=2
6. Finding Possible Integral Values for Radii:
- The integral pairs (R1,R2) that satisfy R1R2=2 are:
- (1,2)
- (2,1)
7. Substituting Back to Find d2:
- Let's use R1=1 and R2=2:
- Substitute into Equation 1:
d2−(1−2)2=9
d2−1=9
d2=10
8. Finding the Reciprocal of the Square of the Distance:
- We need to find 1d2:
1d2=110
Final Answer:
The reciprocal of the square of the distance between the centers of the circles is 110.
- Let the radii of the two circles be R1 and R2.
- The length of the direct common tangent is given as 3 units.
- The length of the transverse common tangent is given as 1 unit.
- The formula for the length of the direct common tangent Ld is:
Ld=√d2−(R1−R2)2
- The formula for the length of the transverse common tangent Lt is:
Lt=√d2−(R1+R2)2
- Here, d is the distance between the centers of the circles.
- From the direct common tangent:
√d2−(R1−R2)2=3
Squaring both sides:
d2−(R1−R2)2=9(Equation 1)
√d2−(R1+R2)2=1
Squaring both sides:
d2−(R1+R2)2=1(Equation 2)
- Subtract Equation 2 from Equation 1:
(d2−(R1−R2)2)−(d2−(R1+R2)2)=9−1
- This simplifies to:
(R1+R2)2−(R1−R2)2=8
- Expanding both squares:
(R21+2R1R2+R22)−(R21−2R1R2+R22)=8
- Simplifying gives:
4R1R2=8
- Thus:
R1R2=2
- The integral pairs (R1,R2) that satisfy R1R2=2 are:
- (1,2)
- (2,1)
- Let's use R1=1 and R2=2:
- Substitute into Equation 1:
d2−(1−2)2=9
d2−1=9
d2=10
- We need to find 1d2:
1d2=110
The reciprocal of the square of the distance between the centers of the circles is 110.
Similar Questions
In figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB=CD

View SolutionIn figure, AB and CD are common tangents to two circles of equal radii. Prove that AB=CD.

View SolutionIn the figure given below, AC is a transverse common tangent to two circles with centres P and Q and of radii 6 cm and 3 cm respectively.
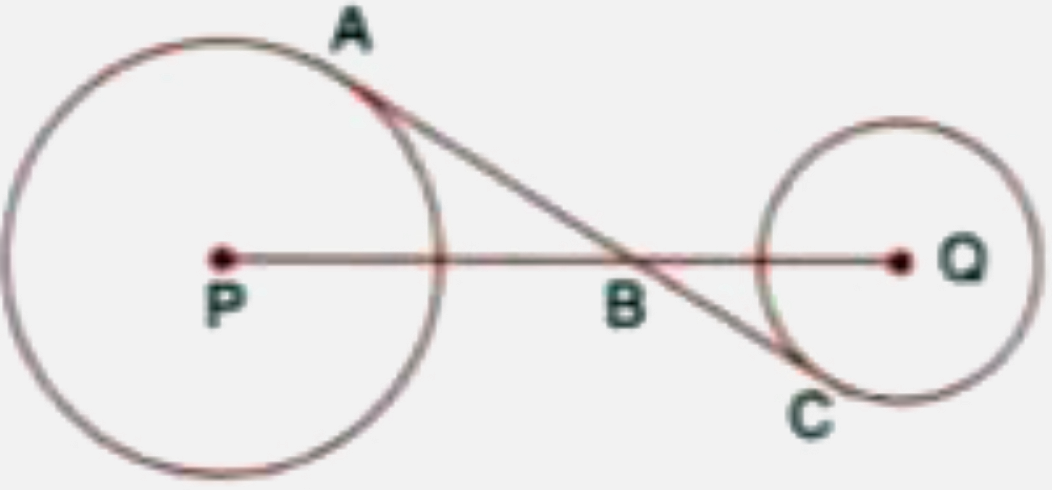
Given that AB=8 cm calculate PQ.
View SolutionWhat is the distance between two parallel tangents of a circle of radius 4 cm?
View SolutionWhat is the distance between two parallel tangents to a circle of radius 5 cm?
View SolutionA circle of radius 2 units is touching both the axes and a circle with centre at (6,5). The distance between their centres is
View SolutionTwo circles of radii 10 cm and 8 cm intersect and the length of the common chord is 12cm. Find the distance between their centres.
View SolutionIf the length of the tangents from P(1, 3) and Q (3, 7) to a circle are √2 units and √18 units respectively, then the length of the tangent from R(7, 15) to the same circle is
View SolutionLet P and Q be 2 circles externally touhing each other at point X. Line segment AB is a direct common tangent to circle P and Q at points A and B respectively. Another common tangent to P and Q at X intersects line AB at a point Y. If BY = 10 units and the radius of P is 9 units, then the value of the reciprocal of the radius of the radius of the circle Q is equal to
View SolutionTwo circles of radii 10 cm and 17 cm . Intersecting each other at two points and the distances between their centres is 21 cm . Find the length of the common chords.
View Solution
