Consider a thin conducting shell of radius carrying total charge . Two point charges and are placed on points and , which are at a distances of and from the center of the cell respectively as shown in the figure. If the cell is earthed how much charge will flow to the earth?

The correct Answer is:A
Since shell is earthed its potential is zero
Hence will flow to the earth

Similar Questions
A thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R2 from the centre of the shell is
View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R/2 from the centre of the shell is
View SolutionTwo concentric conducting shells of radii R and 2R are having charges Q and -2Q respectively.In a region r
View SolutionInside a charged thin conducting shell of radius R, a point charge +Q is placed as shown in figure potential of shell may be
 View Solution
View SolutionA conducting shell of radius R carries charge–Q. A point charge +Q is placed at the centre of shell. The electric field E varies with distance r (from the centre of the shell) as :
View SolutionA conducting shell of radius R carries charge −Q. A point charge +Q is placed at the centre. The electric field E varies with distance r (from the centre of the shell) as
View SolutionA conducting sphere of radius R, carrying charge Q, lies inside uncharged conducting shell of radius 2R. If they are joined by a metal wire,
View SolutionA point charge q is placed at some distance d away from the centre of a grounded conducting sphere of radius r, as shown in the figure. The charge that flows the earth to the sphere is
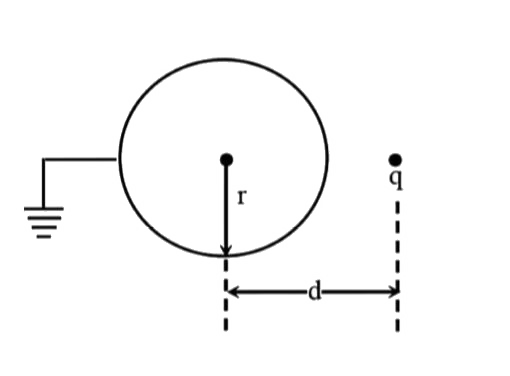 View Solution
View SolutionA conducting sphere of radius R and carrying a charge Q is joined to an uncharged conducting sphere of radius 2R. The charge flowing between them will be
View SolutionA point charge Q is placed inside a conducting spherical shell of inner radius 3R and outer radius 5R at a distance R from the centre of the shell. The electric potential at the centre of the shell will be
View Solution

