A bullet of mass 2g travelling at a speed of 500m/s is fired into a ballistic pendulum of mass 1.0kg suspended from a cord 1.0m long. The bullet penetrates the pendulum and emerges with a velocity of 100m/s. Through what vertical height will the pendulum rise?
To solve the problem step by step, we will use the principles of conservation of momentum and energy.
Step 1: Understand the Problem
We have a bullet of mass mb=2g=0.002kg traveling at a speed of vb=500m/s. It penetrates a ballistic pendulum of mass mp=1.0kg and emerges with a speed of v′b=100m/s. We need to find the height h to which the pendulum rises after the bullet passes through it.
Step 2: Apply Conservation of Momentum
Before the collision, the momentum of the system is only due to the bullet since the pendulum is at rest.
Initial momentum of the bullet:
pinitial=mb⋅vb=0.002kg⋅500m/s=1kg m/s
After the bullet passes through the pendulum, the final momentum of the system (bullet + pendulum) is:
pfinal=mb⋅v′b+mp⋅vp
Where vp is the velocity of the pendulum after the bullet passes through it.
Step 3: Set Up the Momentum Equation
Using conservation of momentum:
pinitial=pfinal
1kg m/s=(0.002kg⋅100m/s)+(1.0kg⋅vp)
Calculating the bullet's momentum after it exits:
0.002⋅100=0.2kg m/s
Now substituting this into the momentum equation:
1=0.2+1.0⋅vp
1−0.2=vp
vp=0.8m/s
Step 4: Calculate the Kinetic Energy of the Pendulum
The kinetic energy KE of the pendulum just after the bullet passes through is given by:
KE=12mpv2p
Substituting the values:
KE=12⋅1.0⋅(0.8)2=12⋅1.0⋅0.64=0.32J
Step 5: Set Up the Potential Energy Equation
At the maximum height h, all kinetic energy will be converted into potential energy PE:
PE=mpgh
Where g=9.8m/s2. Setting KE=PE:
0.32=1.0⋅9.8⋅h
h=0.329.8≈0.03265m
Step 6: Final Answer
The pendulum will rise to a height of approximately:
h≈0.033m or 3.3cm
We have a bullet of mass mb=2g=0.002kg traveling at a speed of vb=500m/s. It penetrates a ballistic pendulum of mass mp=1.0kg and emerges with a speed of v′b=100m/s. We need to find the height h to which the pendulum rises after the bullet passes through it.
Before the collision, the momentum of the system is only due to the bullet since the pendulum is at rest.
pinitial=mb⋅vb=0.002kg⋅500m/s=1kg m/s
pfinal=mb⋅v′b+mp⋅vp
Where vp is the velocity of the pendulum after the bullet passes through it.
Using conservation of momentum:
pinitial=pfinal
1kg m/s=(0.002kg⋅100m/s)+(1.0kg⋅vp)
Calculating the bullet's momentum after it exits:
0.002⋅100=0.2kg m/s
Now substituting this into the momentum equation:
1=0.2+1.0⋅vp
1−0.2=vp
vp=0.8m/s
The kinetic energy KE of the pendulum just after the bullet passes through is given by:
KE=12mpv2p
Substituting the values:
KE=12⋅1.0⋅(0.8)2=12⋅1.0⋅0.64=0.32J
At the maximum height h, all kinetic energy will be converted into potential energy PE:
PE=mpgh
Where g=9.8m/s2. Setting KE=PE:
0.32=1.0⋅9.8⋅h
h=0.329.8≈0.03265m
The pendulum will rise to a height of approximately:
h≈0.033m or 3.3cm
Topper's Solved these Questions
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Subjective
Explore 23 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Single Correct
Explore 141 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Exercise 1.2
Explore 23 Videos
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
Similar Questions
A bullet of mass 20 g moving horizontally at a speed of 300 m/s is fired into a wooden block of mass 500 g suspended by a long string. The bullet crosses the block and emerges on the other side. If the centre of mass of the block rises through a height of 20.0 cm, find the speed of the bullet as it emerges from the block.
View SolutionA bullet of mass 25 g is fired horizontally into a ballistic pendulum of mas 5.0 kg and gets embedded in it figure. If the centre of the pendulum rises by a distance of 10 cm, find the speed of the bullet.
View SolutionA bullet of mass 0.01kg and travelling at a speed of 500ms−1 strikes a block of mass 2kg which is suspended by a string of length 5m. The centre of gravity of the block is found to raise a vertical distance of 0.2m. What is the speed of the bullet after it emerges from the block?
View SolutionA bullet of mass 0.01 kg and travelling at a speed of 500 m/s strikes a block of mass 2 kg which is suspended by a string of length 5m. The center of gravity of the block is found to rise a vertical distance of 0.1m, figure. What is the speed of the bullet after it emerges from the block ? (g=9.8m/s2).
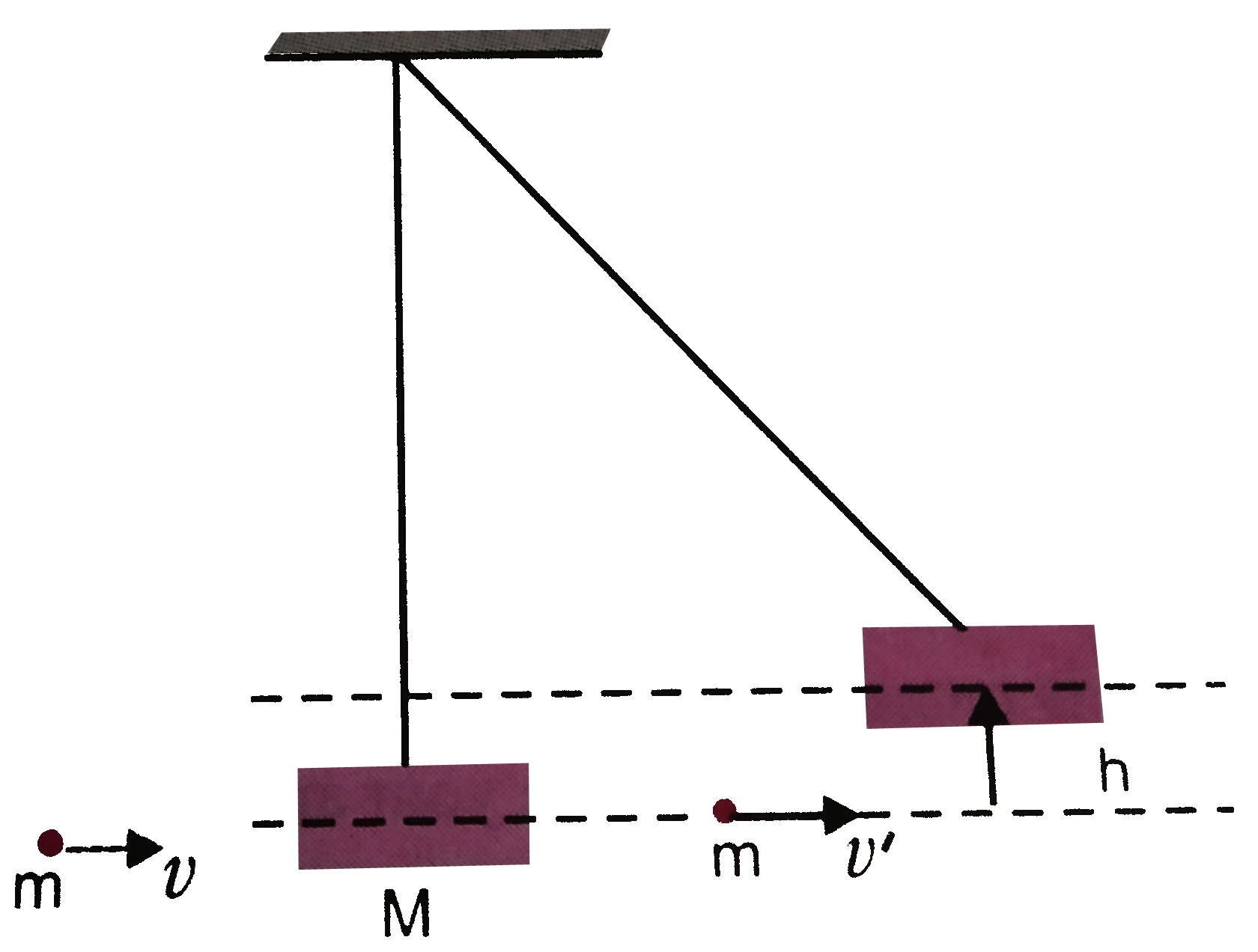
View SolutionA bullet of mass 20 g travelling horizontally with a speed of 500 m/s passes through a wooden block of mass 10.0 kg initially at rest on a level surface. The bulet emerges with speed of 100 m/s and the block slides 20 cm on the surface before coming to rest. Find the friction cioefficient between the block and the surface figure.

View SolutionA bullet of mass 0.1 kg is fired with a speed of 100 m/sec , the mass of gun is 50 kg . The velocity of recoil is
View SolutionA bullet of mass 0.1 kg is fired with a speed of 100 m/sec , the mass of gun is 50 kg . The velocity of recoil is
View SolutionA bullet of mass 10 g is fired from a gun of mass 1 kg with recoil velocity of gun 5 m/s. The muzzle velocity will be
View SolutionA man fires a bullet of mass 200 g at a speed of 5 m/s . The gun is of one kg mass. by what velocity the gun rebounds backwards
View SolutionA bullet of mass 0.04 kg moving with a speed of 600 m/s penetrates a heavy wooden block. It stops after a penetration of 500 cm. The resistive force exerted by the block on the bullet is
View Solution