Two identical spheres S1 and S2 out of which S1 is placed on the insulating horizontal surface and S2 hangs from an insulating string. If both were given same quantity of heat. Then:
temperature of S1 will increase more than S2
temperature of S2 will increase more than S1
Heat given only increases internal energy
Heat given not only increases internal energy but goes in other forms also.
The correct Answer is:B, D
To solve the problem, we need to analyze the situation of two identical spheres S1 and S2 when they are given the same quantity of heat.
1. Understanding the Setup:
- Sphere S1 is placed on an insulating horizontal surface.
- Sphere S2 is hanging from an insulating string.
- Both spheres are identical and are given the same quantity of heat.
Hint: Visualize the setup and the forces acting on each sphere.
2. Effect of Heat on the Spheres:
- When heat is added to a substance, its temperature increases, and it may expand.
- The heat added to each sphere will cause them to expand, increasing their radius.
Hint: Recall the concept of thermal expansion and how heat affects the dimensions of solids.
3. Change in Potential Energy:
- For S1 (on the surface), as it expands, its center of mass remains at the same level (since it is on a horizontal surface), and thus its potential energy does not change significantly.
- For S2 (hanging), as it expands, its center of mass will move upward, which means its potential energy increases.
Hint: Consider how the position of the center of mass affects potential energy in both cases.
4. Heat Distribution:
- The heat given to S1 primarily increases its internal energy (temperature) since there is no change in height.
- The heat given to S2 not only increases its internal energy but also does work against gravity to raise its center of mass, thus increasing its potential energy.
Hint: Think about how energy conservation applies here and how heat can be converted into different forms of energy.
5. Conclusion:
- Since S2 has to do work to raise its center of mass, the effective increase in internal energy (temperature) will be less than that of S1.
- Therefore, the temperature of S2 will increase less than that of S1.
Hint: Compare the net heat used for internal energy increase in both spheres.
Final Answer:
- The temperature of sphere S2 will increase less than that of sphere S1 due to the work done against gravity.
- Sphere S1 is placed on an insulating horizontal surface.
- Sphere S2 is hanging from an insulating string.
- Both spheres are identical and are given the same quantity of heat.
- When heat is added to a substance, its temperature increases, and it may expand.
- The heat added to each sphere will cause them to expand, increasing their radius.
- For S1 (on the surface), as it expands, its center of mass remains at the same level (since it is on a horizontal surface), and thus its potential energy does not change significantly.
- For S2 (hanging), as it expands, its center of mass will move upward, which means its potential energy increases.
- The heat given to S1 primarily increases its internal energy (temperature) since there is no change in height.
- The heat given to S2 not only increases its internal energy but also does work against gravity to raise its center of mass, thus increasing its potential energy.
- Since S2 has to do work to raise its center of mass, the effective increase in internal energy (temperature) will be less than that of S1.
- Therefore, the temperature of S2 will increase less than that of S1.
- The temperature of sphere S2 will increase less than that of sphere S1 due to the work done against gravity.
Similar Questions
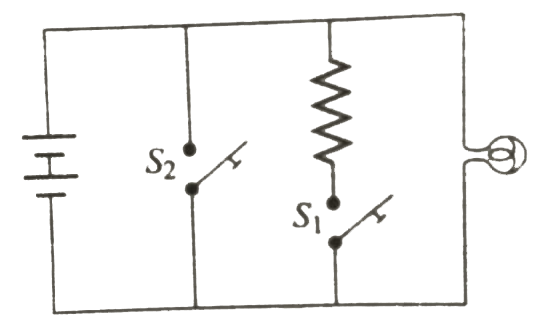
Which of two switches S1andS2 shown in Fig. 7.31 will produce short - circuiting?
 View Solution
View SolutionTwo metallic spheres S1andS2 are made of the same material and have got identical surface finish. The mass of S1 is thrice that of S2. Both the spheres are heated to the same high temperature and placed in the same room having lower temperature but are thermally insulated from each other. the ratio of the initial rate of cooling of S1 to that of S2 is
(a)13(b)1√3(c)√31(d)(13)13View SolutionS1 and S2 are two equipotential surfaces on which the potentials are not equal
View SolutionA conducting sphere S1 of radius r is attached to an insulating handle. Another conduction sphere S2 of radius R is mounted on an insulating stand. S2 is initially uncharged. S1 is given a charge Q brought into contact with S2 and removed. S1 is recharge such that the charge on it is again Q and it is again brought into contact with S2 and removed. This procedure is repeated n times.
a. Find the electrostatic energy of S2 after n such contacts with S1.
b. What is the limiting value of this energy as n→∞ ?View SolutionTwo positively charged sphere of masses m1 and m2 are suspended from a common point at the ceiling by identical insulating massless strings of length l. Charges on the two spheres are q1 and q2 respectively. Equilibrium both strings make the same angle θ with the vertical. then
View SolutionTwo point sources S1 and S2 are 24 cm apart. What should a convex lens of focal length 9 cm be placed between them so that the images of both sources formed at the same place ?
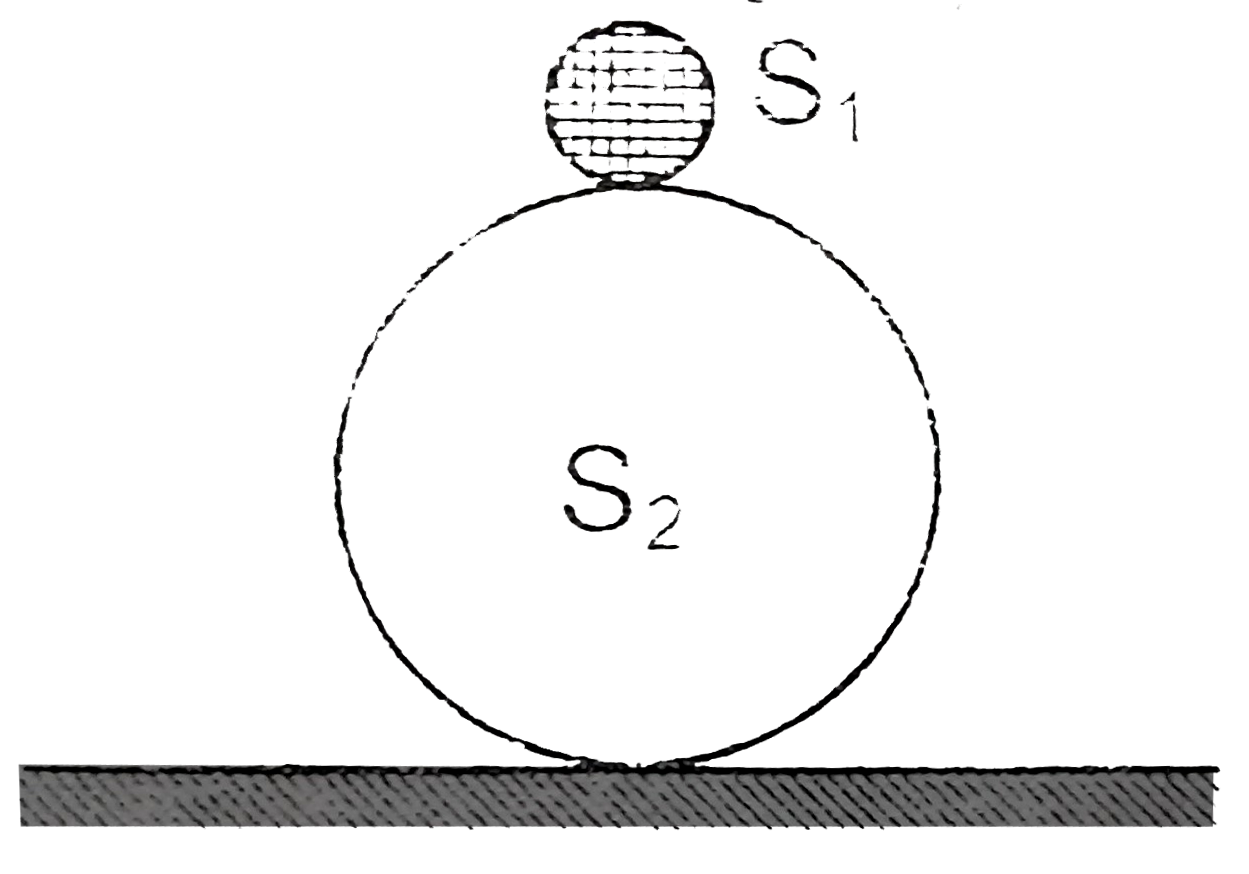
View SolutionS2 is a fixed rough sphere and S1 is a uniform solid sphere S1 is given a negligible velocity, So that at starts moving on the sphere S2, It rolls without slipping. Find the angle formed with the vertical, by the line joining the centres of S1 and S2 when S1 leaves S2
 View Solution
View SolutionTwo different sound sources s1ands2 have frequencies ratio 1:2. Source s, is approaching towards an observer and s2 is receding from the same observer. Speeds of both s1ands2 are the same and equal to v. speed of sound in air in 300 m/s. If no beats are heard by the observer the value of V is 1
View SolutionTwo identical sounds s1ands2 reach at a point P phase. The resultant loudness at a point P is not higher than the loudness of s1. The value of n is
View SolutionConsider two coherent, monochromatic (wavelength λ) sources S1andS2, separated by a distance d. The ratio of intensities of S1 and that of S2 (which is responsible for interference at point P, where detector is located) is 4. The distance of point P from S1 is (if the resultant intensity at point P is equal to 94 times of intensity of S1) (Given : ∠S2S1P=90∘,d>0andn is a positive integer)
View Solution

