Two different sound sources s1ands2 have frequencies ratio 1:2. Source s, is approaching towards an observer and s2 is receding from the same observer. Speeds of both s1ands2 are the same and equal to v. speed of sound in air in 300 m/s. If no beats are heard by the observer the value of V is 1
125 m/s
100 m/s
75 m/s
50 m/s
The correct Answer is:B
To solve the problem, we will use the Doppler effect to find the speed V of the sound sources s1 and s2 given their frequency ratio and the conditions of the observer.
1. Identify the Frequencies:
Let the frequency of source s1 be f and the frequency of source s2 be 2f (since the ratio is 1:2).
2. Doppler Effect for Approaching Source:
When source s1 is approaching the observer, the observed frequency f′ can be calculated using the Doppler effect formula:
f′=fvv−V
where v is the speed of sound in air (300 m/s) and V is the speed of source s1.
3. Doppler Effect for Receding Source:
For source s2 which is receding from the observer, the observed frequency f′′ is given by:
f′′=2fvv+V
4. Condition for No Beats:
The condition for no beats to be heard by the observer is that the observed frequencies must be equal:
f′=f′′
Substituting the expressions for f′ and f′′:
fvv−V=2fvv+V
5. Canceling f:
Since f is common on both sides, we can cancel it out (assuming f≠0):
vv−V=2vv+V
6. Cross Multiplying:
Cross multiplying gives:
v(v+V)=2v(v−V)
7. Expanding Both Sides:
Expanding both sides results in:
v2+vV=2v2−2vV
8. Rearranging the Equation:
Rearranging gives:
vV+2vV=2v2−v2
Simplifying:
3vV=v2
9. Solving for V:
Dividing both sides by v (assuming v≠0):
3V=v
Thus,
V=v3
10. Substituting the Value of v:
Given v=300m/s:
V=3003=100m/s
Final Answer:
The value of V is 100m/s.
Let the frequency of source s1 be f and the frequency of source s2 be 2f (since the ratio is 1:2).
When source s1 is approaching the observer, the observed frequency f′ can be calculated using the Doppler effect formula:
f′=fvv−V
where v is the speed of sound in air (300 m/s) and V is the speed of source s1.
For source s2 which is receding from the observer, the observed frequency f′′ is given by:
f′′=2fvv+V
The condition for no beats to be heard by the observer is that the observed frequencies must be equal:
f′=f′′
Substituting the expressions for f′ and f′′:
fvv−V=2fvv+V
Since f is common on both sides, we can cancel it out (assuming f≠0):
vv−V=2vv+V
Cross multiplying gives:
v(v+V)=2v(v−V)
Expanding both sides results in:
v2+vV=2v2−2vV
Rearranging gives:
vV+2vV=2v2−v2
Simplifying:
3vV=v2
Dividing both sides by v (assuming v≠0):
3V=v
Thus,
V=v3
Given v=300m/s:
V=3003=100m/s
The value of V is 100m/s.
Topper's Solved these Questions
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - LECTURE SHEET (EXERCISE-VI (LEVEL-II(ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS))
12 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - LECTURE SHEET (EXERCISE-VI (LEVEL-II(ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS))
4 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - LECTURE SHEET (EXERCISE-V (LEVEL-II(ADVANCED) INTEGER TYPE QUESTIONS))
3 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -3
66 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
97 Videos
Similar Questions
A source is moving towards an observer with a speed of 20 m / s and having frequency of 240 Hz . The observer is now moving towards the source with a speed of 20 m / s . Apparent frequency heard by observer, if velocity of sound is 340 m / s , is
View SolutionA source of sound is travelling towards a stationary observer. The frequency of sound heard by the observer is 25% more that the actual frequency. If the speed of sound is v, that of the source is
View Solution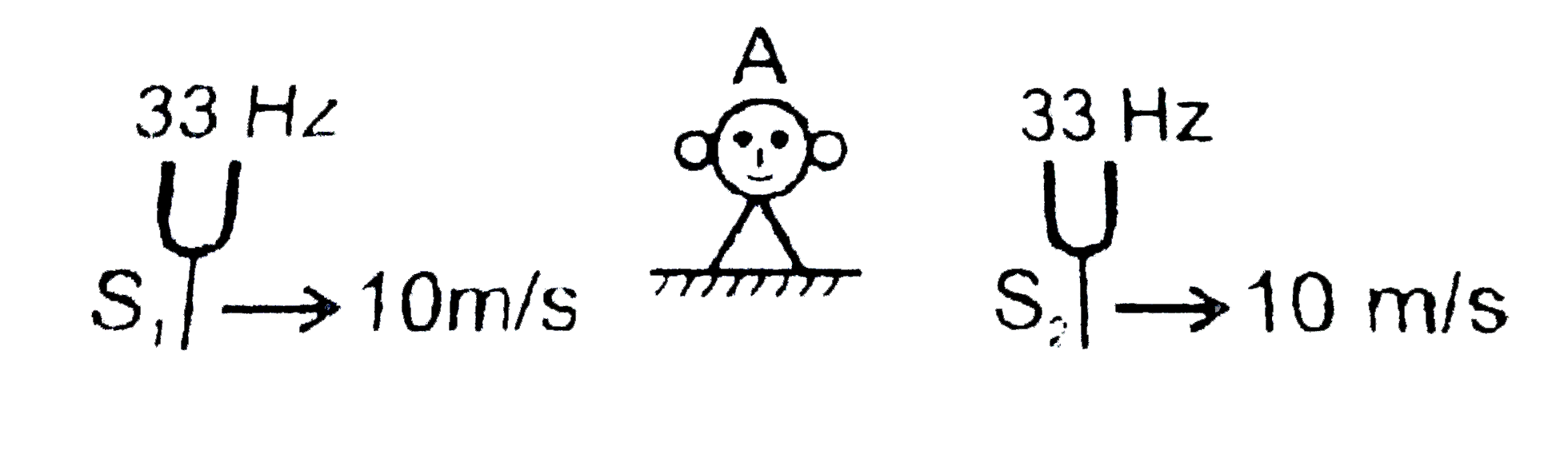
Observer A is at rest. Source S1 is moving towards observer A and source S2 is moving away from observer A. velocity of sound is 330msec. β= beat frequency heard per second by A. Approximate value of β is:
View SolutionOne train is approaching an observer at rest and another train is receding from him with the same velocity 4m/s . Both trains blow whistles of same frequency of 243HZ . The beat frequency in HZ as heard by observer is (speed of sound in air = 320m/s)
View SolutionConsider the vehicle emitting sound wave of frequency 700 Hz moving towards an observer at a speed 22ms−1 . Assuming the observer to be at rest, and speed of sound to be 330ms−1 , the frequency of sound as measured by the observer is
View SolutionA source of sound of frequency 500 Hz is moving towards an observer with velocity 30 m/s . The speed of sound is 330 m/s . the frequency heard by the observer will be
View SolutionA source of sound of frequency f is approaching towards a wall with speed υs . Speed of sound is υ . Three observers O1 , O2 and O3 are at different locations as shown . Find the beat frequency as observed by three different observers.

View SolutionTo an observer, the pitch of a stationary source of sound appears to be reduced by 20%. If the speed of sound is 340m/s then speed and direction of the observer is
View SolutionAn observer moves on the same line on which two sources of sound of frequency 660Hz are present. The observer observes beat frequency of 10Hz. If speed of sound is 300m/s then speed of the observer is:
View SolutionAt t=0 , observer and source are at same place. Now the source is projected with velocity 60√2m/s at 45∘ . Natural frequency of source is 1000 Hz.find the frequency heard by the observer at t=2s. Take speed of sound = 340 m/s
View Solution
