A neutron having kinetic energy E0 collides with singly ionised He atom at rest and move along initial direction. Which of the following statement(s) is/are true for the above mentioned collision.
Collision will be perfectly inelastic if E0=17eV
Collision will be perfectly inelastic is E0=8.16eV
If E0= then ploton of wavelength λ=500m is observed just after the collision if E0=8.16eV.
Perfectly elastic collision is not possible.
The correct Answer is:A, B, D
To solve the problem, we will analyze the collision between a neutron with kinetic energy E0 and a singly ionized helium atom at rest. We will apply the principles of conservation of momentum and conservation of energy.
1. Identify the masses involved:
- Let the mass of the neutron be m.
- The mass of the singly ionized helium atom (which has 2 protons and 2 neutrons) is approximately 4m.
2. Initial Conditions:
- The neutron is moving with an initial velocity v0 and has kinetic energy E0=12mv20.
- The helium atom is at rest, so its initial velocity is 0.
3. Conservation of Momentum:
- Before the collision, the total momentum pi is given by:
pi=mv0+0=mv0
- After the collision, let the final velocity of the system be v. The total momentum pf after the collision is:
pf=(m+4m)v=5mv
- By conservation of momentum:
mv0=5mv⟹v=v05
4. Conservation of Energy:
- The initial kinetic energy of the neutron is:
KEi=12mv20
- After the collision, the kinetic energy of the system is:
KEf=12(5m)v2=5m2(v05)2=5m2⋅v2025=mv2010
- The change in energy (if any) due to the collision is:
ΔE=KEi−KEf=12mv20−mv2010=5mv2010−mv2010=4mv2010=2mv205
5. Relate ΔE to E0:
- Since E0=12mv20, we can express ΔE in terms of E0:
ΔE=25E0
6. Analyzing the statements:
- If E0=17 eV, then ΔE=25×17=6.8 eV (not zero, hence the collision is inelastic).
- If E0=8.16 eV, then ΔE=25×8.16=3.264 eV (again not zero, hence the collision is inelastic).
- The photon emitted has energy equal to ΔE, which can be checked against the wavelength given in the problem.
7. Conclusion:
- The collision is not perfectly elastic since ΔE≠0.
- The statements regarding the energy values and the nature of the collision can be verified based on the calculations above.
- Let the mass of the neutron be m.
- The mass of the singly ionized helium atom (which has 2 protons and 2 neutrons) is approximately 4m.
- The neutron is moving with an initial velocity v0 and has kinetic energy E0=12mv20.
- The helium atom is at rest, so its initial velocity is 0.
- Before the collision, the total momentum pi is given by:
pi=mv0+0=mv0
- After the collision, let the final velocity of the system be v. The total momentum pf after the collision is:
pf=(m+4m)v=5mv
- By conservation of momentum:
mv0=5mv⟹v=v05
- The initial kinetic energy of the neutron is:
KEi=12mv20
- After the collision, the kinetic energy of the system is:
KEf=12(5m)v2=5m2(v05)2=5m2⋅v2025=mv2010
- The change in energy (if any) due to the collision is:
ΔE=KEi−KEf=12mv20−mv2010=5mv2010−mv2010=4mv2010=2mv205
- Since E0=12mv20, we can express ΔE in terms of E0:
ΔE=25E0
- If E0=17 eV, then ΔE=25×17=6.8 eV (not zero, hence the collision is inelastic).
- If E0=8.16 eV, then ΔE=25×8.16=3.264 eV (again not zero, hence the collision is inelastic).
- The photon emitted has energy equal to ΔE, which can be checked against the wavelength given in the problem.
- The collision is not perfectly elastic since ΔE≠0.
- The statements regarding the energy values and the nature of the collision can be verified based on the calculations above.
Similar Questions
Which of the following statements about kinetic energy (K.E.) is true?
View SolutionFigure shows a plot of the potential energy as a function of x for a particle moving along the x-axis. Which of the following statement(s) is/are true?
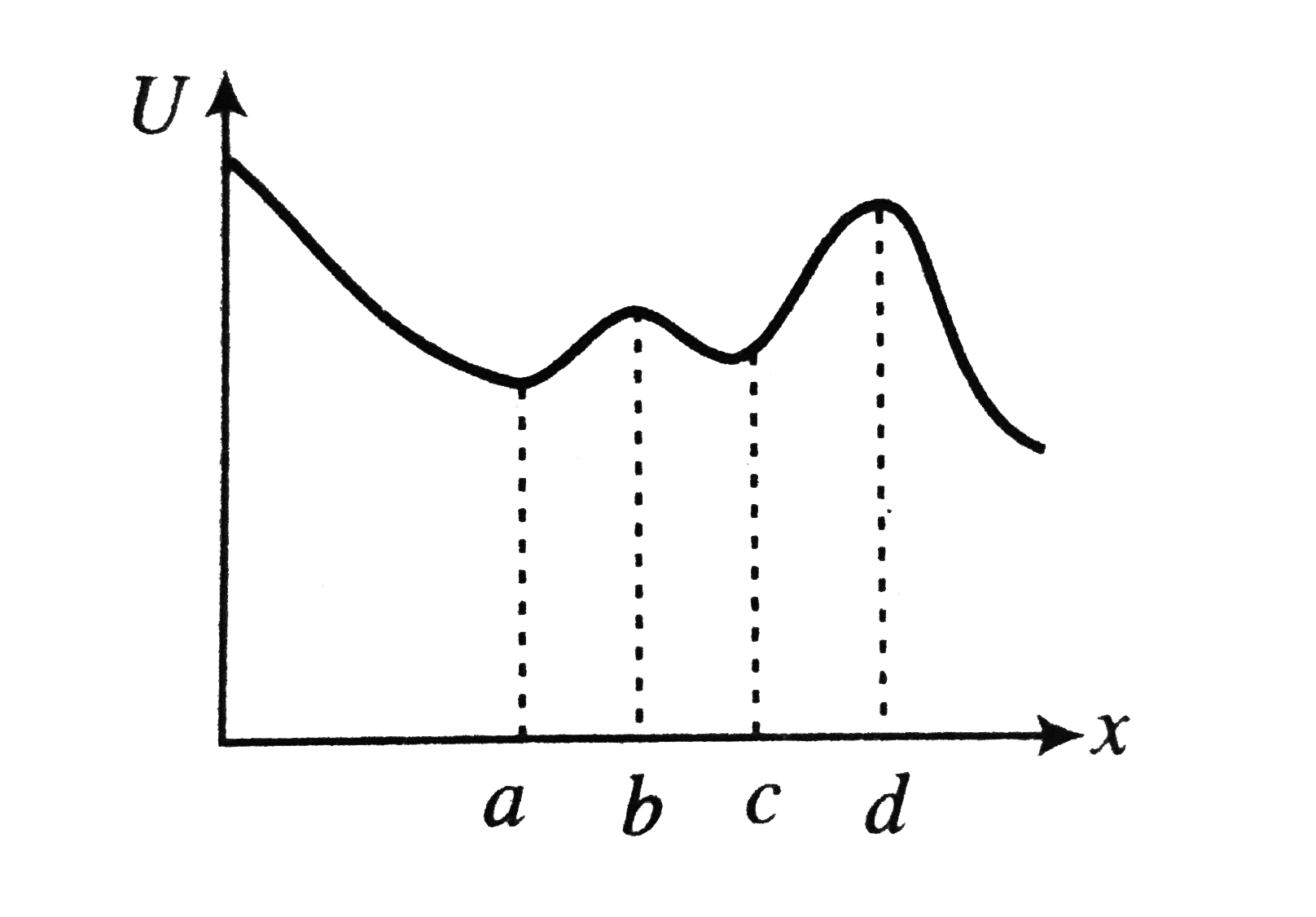 View Solution
View SolutionFigure shows a plot of the potential energy as a function of x for a particle moving along the x-axis. Which of the following statement(s) is/are true?
 View Solution
View SolutionA neutron of kinetic energy 65 eV collides inelastically with a singly ionised helium atom at rest. It is scattered at an angle 90∘ with respect to original direction. If the energy of scattered neutron is 6.36 eV, find the frequency of emitted radiation from the helium atom after suffering collision.
View SolutionA hydrogen atom having kinetic energy E collides with a stationary hydrogen atom. Assume all motions are taking place along the line of motion of the moving hydrogen atom. For this situation, mark out the correct statement (s).
View SolutionA neutron having kinetic energy 12.5eV collides with a hydrogen atom at rest negect the difference in mass between the neutron and the hydrogen atom and assume that the neutron does not leave its of motion find the posible kinetic energy of the neutron after the event
View SolutionThe ground state energy of hydrogen atom is −13.6eV. Consider an electronic state Ψ of He+ whose energy, azimuthal quantum number and magnetic quantum number are −3.4eV,2 and 0, respectively. Which of the following statement(s) is(are) true for the state Ψ?
View SolutionThree blocks A, B and C each of mass m are placed on a surface as shown in the figure. Blocks B and C are initialyy at rest. Block A is moving to the right with speed v. It collides with block B and stricks to it. The A-B combination collides elastically with block C. Which of the following statement is (are) true about the velocity, of block B and C.
 View Solution
View SolutionA particle of mass m is initially at rest at the origin. It is subjected to a force and starts moving along the x-axis. It kinetic energy K changes with time as dK/dt=γt, where γ is a positive constant of appropriate dimensions. Which of the following statement is (are) true?
View SolutionA point mass of 1kg collides elastically with a stationary point mass of 5 kg. After their collision, the 1kg mass reverses its direction and moves with a speed of 2ms−1. Which of the following statements (s) is (are) correct for the system of these two masses?
View Solution

