A particle of mass m is initially at rest at the origin. It is subjected to a force and starts moving along the x-axis. It kinetic energy K changes with time as where is a positive constant of appropriate dimensions. Which of the following statement is (are) true?
(a)The force applied on the particle is constant
(b)The speed of the particle is proportional to time
(c)The distance of the particle from the origin increases linearly with time
(d)The force is conservative
The correct Answer is:A, B, D
To solve the problem step by step, we will analyze the given information and derive the necessary relationships.
Step 1: Understand the given information
We have a particle of mass m that is initially at rest at the origin. The change in kinetic energy K with respect to time t is given by:
dKdt=γt
where γ is a positive constant.
Step 2: Integrate the kinetic energy change
To find the kinetic energy K as a function of time, we can integrate the expression for dKdt:
dK=γtdt
Integrating both sides from 0 to t:
K(t)−K(0)=∫t0γt′dt′
Since the particle is initially at rest, K(0)=0:
K(t)=∫t0γt′dt′=γ((t′)22)t0=γt22
Step 3: Relate kinetic energy to velocity
The kinetic energy K is also related to the velocity v of the particle:
K=12mv2
Equating the two expressions for kinetic energy:
12mv2=γt22
Multiplying both sides by 2:
mv2=γt2
Dividing by m:
v2=γmt2
Taking the square root:
v=√γmt
Step 4: Analyze the velocity and acceleration
From the expression for velocity:
v=√γmt
we can see that velocity is directly proportional to time t.
Step 5: Find acceleration
Acceleration a is the derivative of velocity with respect to time:
a=dvdt=ddt(√γmt)=√γm
Since a is constant, the force F acting on the particle can be calculated using Newton's second law:
F=ma=m⋅√γm=√γm
This indicates that the force is constant.
Step 6: Determine the displacement
To find the displacement x, we can integrate the velocity:
dx=vdt=√γmtdt
Integrating from 0 to t:
x(t)−x(0)=∫t0√γmt′dt′=√γm((t′)22)t0=√γm⋅t22
Thus:
x(t)=√γ2√mt2
Conclusion
Now we can summarize the findings:
1. The force applied on the particle is constant.
2. The speed of the particle is proportional to time.
3. The distance from the origin increases with the square of time, not linearly.
Final Statements
- The correct statements are:
- The force applied on the particle is constant.
- The speed of the particle is proportional to time.
- The distance of the particle from the origin does not increase linearly with time (it increases with t2).
- The force is conservative.
We have a particle of mass m that is initially at rest at the origin. The change in kinetic energy K with respect to time t is given by:
dKdt=γt
where γ is a positive constant.
To find the kinetic energy K as a function of time, we can integrate the expression for dKdt:
dK=γtdt
Integrating both sides from 0 to t:
K(t)−K(0)=∫t0γt′dt′
Since the particle is initially at rest, K(0)=0:
K(t)=∫t0γt′dt′=γ((t′)22)t0=γt22
The kinetic energy K is also related to the velocity v of the particle:
K=12mv2
Equating the two expressions for kinetic energy:
12mv2=γt22
Multiplying both sides by 2:
mv2=γt2
Dividing by m:
v2=γmt2
Taking the square root:
v=√γmt
From the expression for velocity:
v=√γmt
we can see that velocity is directly proportional to time t.
Acceleration a is the derivative of velocity with respect to time:
a=dvdt=ddt(√γmt)=√γm
Since a is constant, the force F acting on the particle can be calculated using Newton's second law:
F=ma=m⋅√γm=√γm
This indicates that the force is constant.
To find the displacement x, we can integrate the velocity:
dx=vdt=√γmtdt
Integrating from 0 to t:
x(t)−x(0)=∫t0√γmt′dt′=√γm((t′)22)t0=√γm⋅t22
Thus:
x(t)=√γ2√mt2
Now we can summarize the findings:
1. The force applied on the particle is constant.
2. The speed of the particle is proportional to time.
3. The distance from the origin increases with the square of time, not linearly.
- The correct statements are:
- The force applied on the particle is constant.
- The speed of the particle is proportional to time.
- The distance of the particle from the origin does not increase linearly with time (it increases with t2).
- The force is conservative.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - PARAGRAPH QUESTIONS5videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - ASSERTION & REASON TYPE1videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE MAIN (ARCHIVE)53videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)89videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )111videos
GASEOUS STATE & THERMODYNAMICS
Similar Questions
At time t=0s particle starts moving along the x− axis. If its kinetic energy increases uniformly with time 't', the net force acting on it must be proportional to
View SolutionA particle free to move along the (x - axis) hsd potential energy given by U(x)=k[1−exp(−x2)]for−oo≤x≤+oo, where (k) is a positive constant of appropriate dimensions. Then.
View SolutionA particle free to move along the (x - axis) has potential energy given by U(x)=k[1−exp(−x2)]for−oo≤x≤+oo, where (k) is a positive constant of appropriate dimensions. Then.
View SolutionA particle free to move along the x−axis has potential energy given by U(x)=k[1−e−x2] for −∞≤x≤+∞, where k is a positive constant of appropriate dimensions. Then select the incorrect option
View SolutionThe velocity v of a particle of mass is moving along a straight line change with time t as d2vdt2=−Kv where K is a particle constant which of the following statement is correct?
View SolutionThe velocity v of a particle of mass m changes with time t as d2vdt=−kv, where k is constant. Now, which of the following statements is correct?
View SolutionA particle of mass m is at rest at the origin at time t=0 It is subjected to a force F(t)=F0e−bt in the X-direction. Its speed V(t) is depicted by which of the following curves
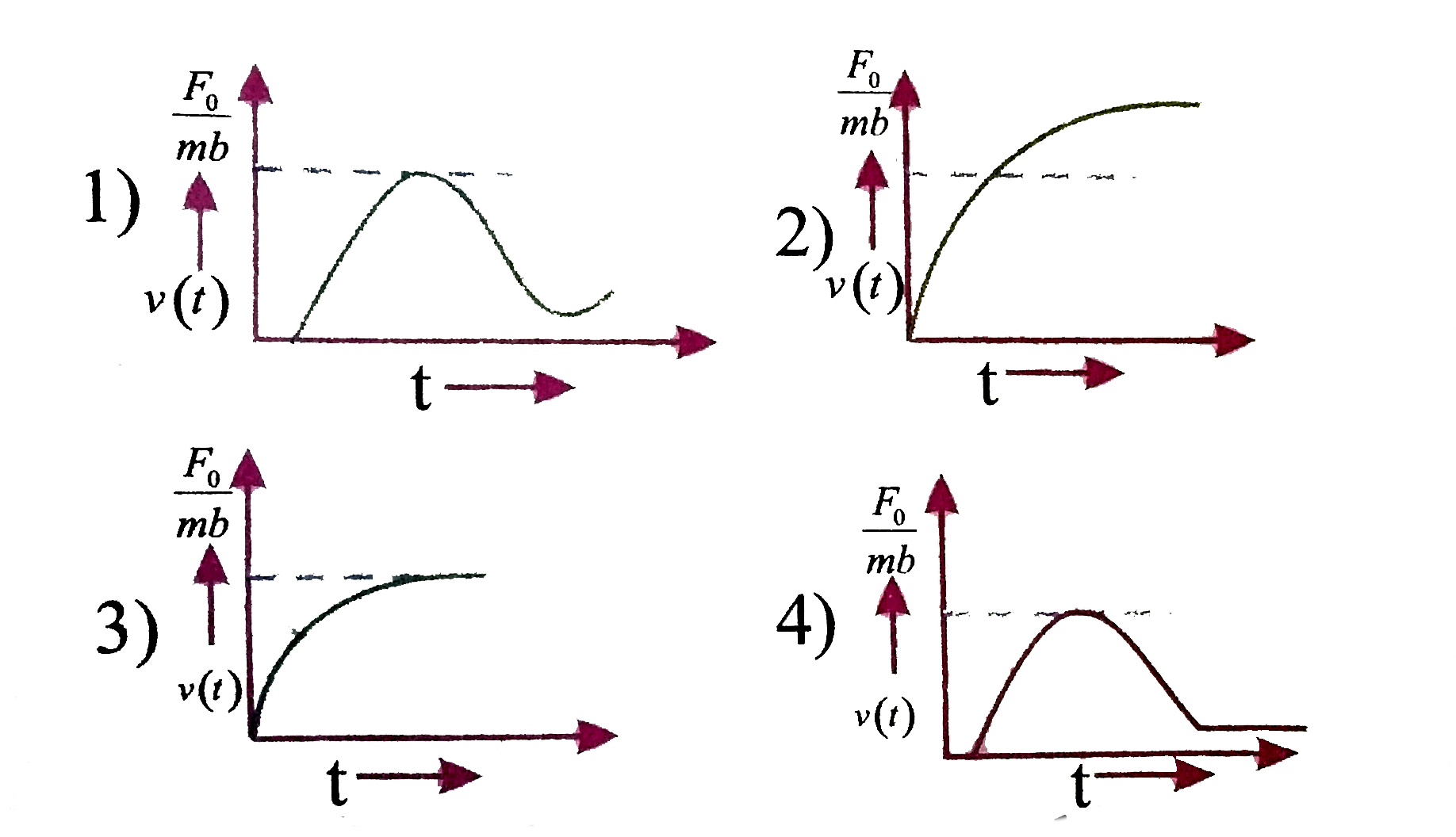 View Solution
View SolutionA particle of mass m is at rest the origin at time t=0 . It is subjected to a force F(t)=F0e−bt in the x - direction. Its speed v(t) is depicted by which of the following curves ?
View SolutionFigure shows a plot of the potential energy as a function of x for a particle moving along the x-axis. Which of the following statement(s) is/are true?
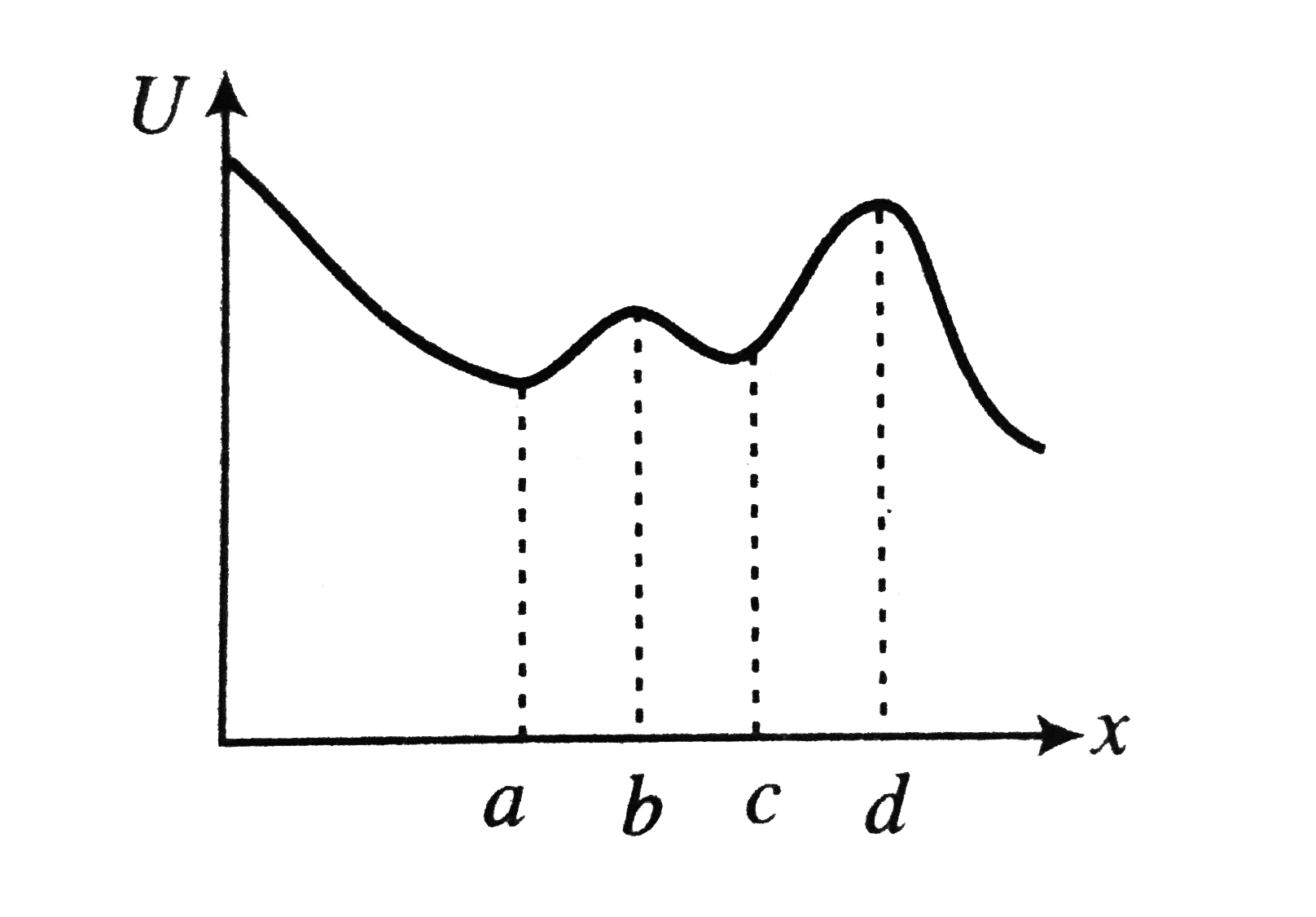 View Solution
View SolutionFigure shows a plot of the potential energy as a function of x for a particle moving along the x-axis. Which of the following statement(s) is/are true?
 View Solution
View Solution

