Two balls & of mass and are kept on a horizontal smooth surface. A is given a velocity towards so that they perform head on collision
If and collision is elastic. A stops and moves with the velocity of after collision
Impulses on and during collision are same in magnitude whether it is elastic or inelastic collision
Impulses on and collision are equal in magnitude only if
If , though impulses are same in magnitude velocity of is still the same direction.
The correct Answer is:A, B, D
To solve the problem of the head-on collision between two balls A and B with masses m1 and m2 respectively, we will analyze the situation step by step.
Step 1: Identify Initial Conditions
Let:
- Mass of ball A = m1
- Mass of ball B = m2
- Initial velocity of ball A = u1=v (given)
- Initial velocity of ball B = u2=0 (at rest)
Step 2: Understand the Type of Collision
The problem states that the collision is elastic. In an elastic collision, both momentum and kinetic energy are conserved.
Step 3: Apply Conservation of Momentum
The principle of conservation of momentum states that the total momentum before the collision is equal to the total momentum after the collision. Mathematically, this can be expressed as:
m1u1+m2u2=m1v1+m2v2
Substituting the values of u1 and u2:
m1v+m2⋅0=m1v1+m2v2
This simplifies to:
m1v=m1v1+m2v2(Equation 1)
Step 4: Apply Conservation of Kinetic Energy
For an elastic collision, the kinetic energy before and after the collision is also conserved:
12m1u21+12m2u22=12m1v21+12m2v22
Substituting the values of u1 and u2:
12m1v2+0=12m1v21+12m2v22
This simplifies to:
m1v2=m1v21+m2v22(Equation 2)
Step 5: Analyze the Case When m1=m2
If m1=m2=m:
From Equation 1:
mv=mv1+mv2⟹v=v1+v2
From Equation 2:
mv2=mv21+mv22⟹v2=v21+v22
Step 6: Solve the Equations
We have two equations:
1. v=v1+v2
2. v2=v21+v22
From the first equation, we can express v2 in terms of v1:
v2=v−v1
Substituting this into the second equation:
v2=v21+(v−v1)2
Expanding the equation:
v2=v21+(v2−2vv1+v21)
Combining like terms:
v2=2v21−2vv1+v2
Cancelling v2 from both sides:
0=2v21−2vv1
Factoring out 2v1:
0=2v1(v1−v)
This gives us two solutions:
1. v1=0 (ball A stops)
2. v1=v (ball B moves with the velocity of A)
Since ball A collides with ball B, the first case is valid, meaning:
- v1=0 (ball A stops)
- v2=v (ball B moves with the velocity of A)
Conclusion
If m1=m2 and the collision is elastic, ball A stops, and ball B moves with the velocity of A after the collision.
Let:
- Mass of ball A = m1
- Mass of ball B = m2
- Initial velocity of ball A = u1=v (given)
- Initial velocity of ball B = u2=0 (at rest)
The problem states that the collision is elastic. In an elastic collision, both momentum and kinetic energy are conserved.
The principle of conservation of momentum states that the total momentum before the collision is equal to the total momentum after the collision. Mathematically, this can be expressed as:
m1u1+m2u2=m1v1+m2v2
Substituting the values of u1 and u2:
m1v+m2⋅0=m1v1+m2v2
This simplifies to:
m1v=m1v1+m2v2(Equation 1)
For an elastic collision, the kinetic energy before and after the collision is also conserved:
12m1u21+12m2u22=12m1v21+12m2v22
Substituting the values of u1 and u2:
12m1v2+0=12m1v21+12m2v22
This simplifies to:
m1v2=m1v21+m2v22(Equation 2)
If m1=m2=m:
From Equation 1:
mv=mv1+mv2⟹v=v1+v2
From Equation 2:
mv2=mv21+mv22⟹v2=v21+v22
We have two equations:
1. v=v1+v2
2. v2=v21+v22
v2=v−v1
Substituting this into the second equation:
v2=v21+(v−v1)2
Expanding the equation:
v2=v21+(v2−2vv1+v21)
Combining like terms:
v2=2v21−2vv1+v2
Cancelling v2 from both sides:
0=2v21−2vv1
Factoring out 2v1:
0=2v1(v1−v)
This gives us two solutions:
1. v1=0 (ball A stops)
2. v1=v (ball B moves with the velocity of A)
- v1=0 (ball A stops)
- v2=v (ball B moves with the velocity of A)
If m1=m2 and the collision is elastic, ball A stops, and ball B moves with the velocity of A after the collision.
Similar Questions
Three balls A,B and C each of mass m and same size,are placed along same line on smooth horizontal surface.A is given a velocity u towards B as shown.If coefficient of restitution for collision between A and B is 12 and between B and C is 13.Assuming all the collisions to be head on choose the correct options: (A) Final velocity of A is u4, (B) Final velocity of B is u4 (C) Final velocity of C is u2, (D) Total energy loss is 516mu2
View SolutionTwo blocks A and B of masses m and 2m are placed on a smooth horizontal surface. Block B is given a speed of 3m/s. Find
(i) The maximum speed of A
(ii) The minimum speed of B.
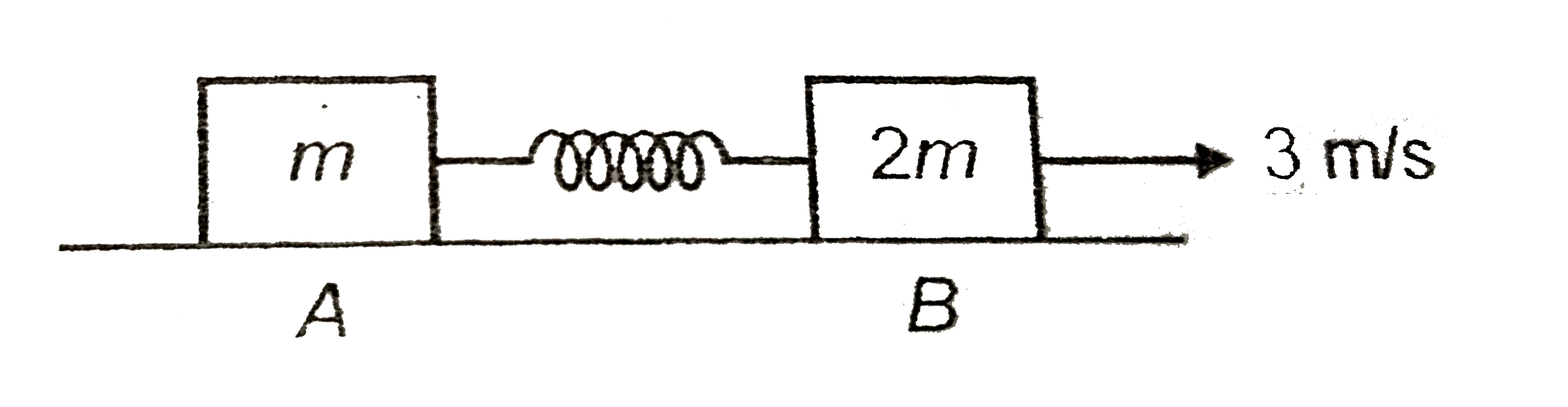 View Solution
View SolutionTwo blocks of masses m1 and m2 are kept on a smooth horizontal table as shown in figure. Block of mass m1 (but not m2 is fastened to the spring. If now both the blocks are pushed to the left so that the spring is compressed a distance d. The amplitude of oscillatin of block of mass m1 after the system is released is
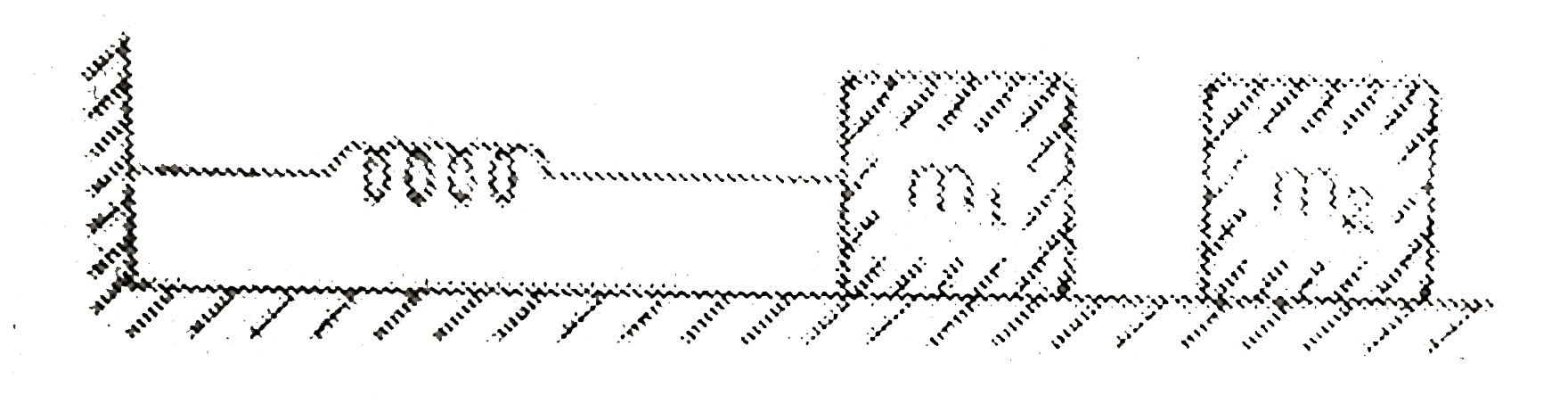 View Solution
View SolutionTwo sphere AandB of masses m1andm2 respectivelly colides. A is at rest initally and B is moving with velocity v along x-axis. After collision B has a velocity v2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction.
View SolutionTwo spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision, B has a velocity v2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction
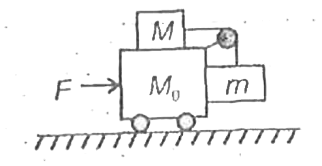
View SolutionTwo blocks of mass M and m are kept on the trolley whose all surfaces are smooth select the correct statement
 View Solution
View SolutionTwo blocks of masses m1 and m2 interconnect with a spring of stiffness K, are kept on as smooth horizontal surface. Find out the ratio of velocity, displacement, kinetic energy and acceleration block with mass m1 of block with mass m2.
View SolutionTwo balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare: Their inertia.
View SolutionTwo balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare: Their momentum.
View SolutionTwo balls marked 1 and 2 of the same mass m and a third ball marked 3 of mass M are arranged over a smooth horizontal surface as shown in the figure. Ball 1 moves with a velocity v1 towards ball 2. All collisions are assumed to be elastic. If M<m, the number of collisions between the balls will be.
 View Solution
View Solution

