Two blocks of mass m1 and m2 (m1<m2) are connected with an ideal spring on a smooth horizontal surface as shown in figure. At t = 0 m1 is at rest and m2 is given a velocity v towards right. At this moment, spring is in its natural length. Then choose the correct alternative :

Block of mass m2 will be finally at rest after some time.
Block of mass m2 will never come to rest.
Both the blocks will be finally at rest.
None of these
If velocity of m2 is zero then by momentum conservation m1v'=m2v
v'=m2vm1
Now, kinetic energy of m1
=12m1v'2=12m1(m2m1)2v2=12(m2m1)m2v2=(m2m1)12m2v2=m2m1× intial kinetic energy
Kinetic energy of m1> initial mechanical of system Henced proved
Topper's Solved these Questions
Similar Questions
Two smooth blocks of mases m1andm2 attached with an ideal spring of stiffness k and kept on hrozontal surface. If m1 is projected with a horizontal velocity v0. Find the maximum compression of the spring.
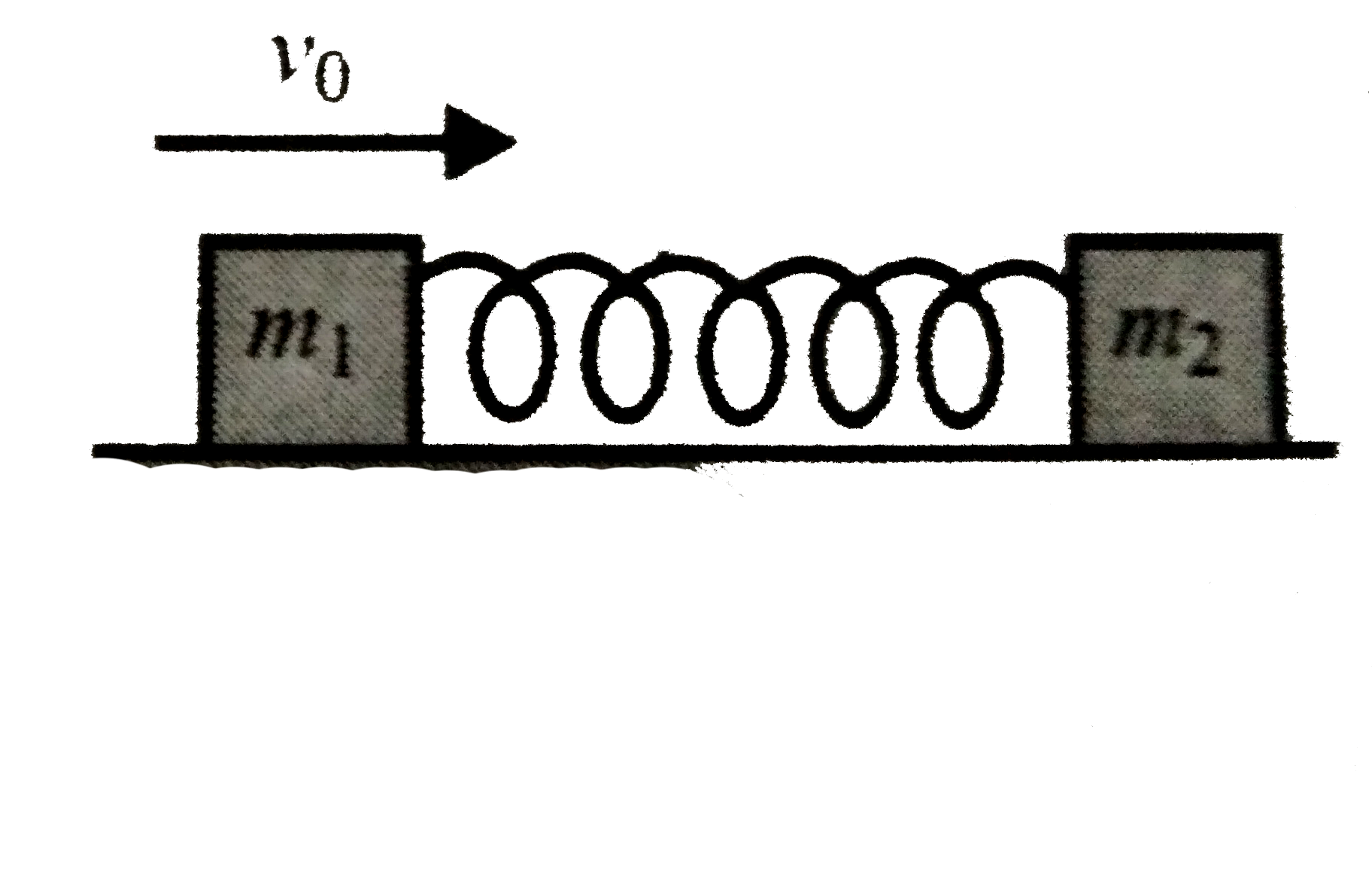 View Solution
View SolutionTwo blocks of masses m1andm2 being connected with a light spring of stiffness k are driven with forces F1andF2 on a smooth horizontal plane.
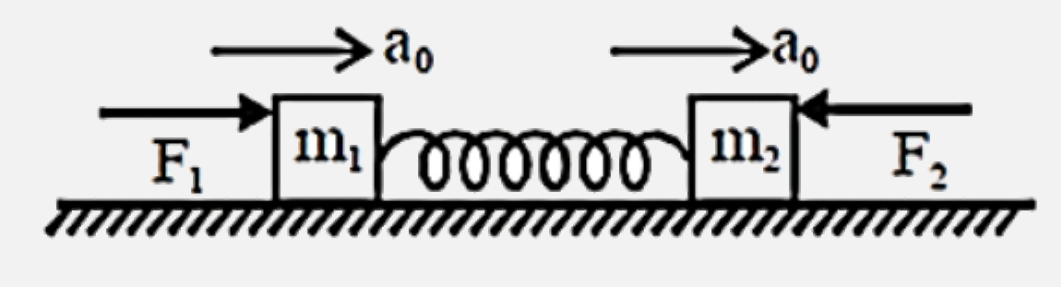 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
There blocks of masses m1 , m2 and m3 are connected by may less unstretchable strings on a smooth surface. Tension T2 is.
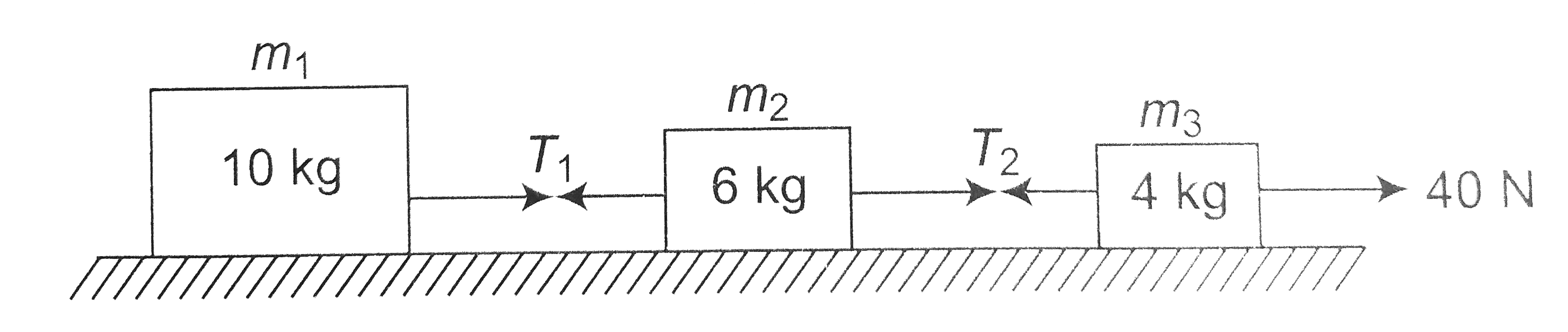 A2.3NB32NC23ND3.2N
A2.3NB32NC23ND3.2N - Question 2 - Select One
Two blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
Athe momentum of each particle remains constant separatelyBthe magnitude of momentums of each body are equal to each otherCthe mechanical energy of system remains constantDboth (C) and (B) are correct - Question 3 - Select One or More
Two blocks of mass m1 and m2, resting on a frictionless table, are connected by a stretched spring and then released -
Aratio of speed of blocks is m2/m1Bratio of kinetic energy of blocks is m2/m1Ccentre of mass will move towards heavier blockDmechanical energy will remain conserve in this process
Two block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:
 View Solution
View Solution
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :View SolutionTwo masses m1 and m2 are accelerated uniformly on a frictionless surface as shown in figure given below. The ratio of the tensions T1T2 is:
 View Solution
View SolutionTwo blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of osciallation is
View SolutionTwo blocks of masses M1 and M2 are connected to each other through a light spring as shown in figure. If we push mass M1 with force F and cause acceleration a1 in mass M1. What will be the magnitude of accleration in M2?
 View Solution
View Solution

