A rod of length l=100cm is fixed at 30cm from both end. If velocity of transverse wave in rod is v(cms−1), then chose the correct option(s)
Fundamental frequencey (in Hz) of transverse wave in rod is v40
Second overtone in rod will 5th harmonic
Frequency of third overtone (in Hz) is 7v/40
Third overtone is5th harmonic
The correct Answer is:A, B, C
To solve the problem, we need to analyze the fixed rod and the transverse waves traveling through it. Here's a step-by-step breakdown of the solution:
Step 1: Understand the Setup
The rod has a total length l=100cm and is fixed at 30cm from both ends. This means that the effective length of the rod that can vibrate is:
L=100cm−30cm−30cm=40cm
Step 2: Identify the Modes of Vibration
The rod is fixed at both ends, which means it can support standing waves. The fundamental frequency (first harmonic) corresponds to one complete wave fitting in the length of the vibrating section of the rod.
Step 3: Fundamental Frequency Calculation
For a rod fixed at both ends, the fundamental frequency f1 is given by:
f1=vλ1
where λ1 is the wavelength of the fundamental mode. For the fundamental mode, the wavelength is twice the length of the vibrating section:
λ1=2L=2×40cm=80cm
Thus, the fundamental frequency is:
f1=v80
Step 4: Determine the Harmonics
The harmonics for a rod fixed at both ends are given by:
fn=n⋅f1=n⋅v80
where n is the harmonic number (1, 2, 3, ...).
Step 5: Identify Overtones
- The first overtone (second harmonic) corresponds to n=2:
f2=2⋅v80=v40
- The second overtone (third harmonic) corresponds to n=3:
f3=3⋅v80
- The third overtone (fourth harmonic) corresponds to n=4:
f4=4⋅v80=v20
Step 6: Find the Specific Frequencies
- The second overtone is the fifth harmonic, which corresponds to n=5:
f5=5⋅v80=5v80=v16
- The third overtone is the sixth harmonic, which corresponds to n=6:
f6=6⋅v80=6v80=3v40
Step 7: Final Answers
- The fundamental frequency is v80.
- The second overtone is the fifth harmonic.
- The frequency of the third overtone is 3v40.
Conclusion
The correct options based on the calculations are:
1. The fundamental frequency is v80.
2. The second overtone is the fifth harmonic.
3. The frequency of the third overtone is 3v40.
The rod has a total length l=100cm and is fixed at 30cm from both ends. This means that the effective length of the rod that can vibrate is:
L=100cm−30cm−30cm=40cm
The rod is fixed at both ends, which means it can support standing waves. The fundamental frequency (first harmonic) corresponds to one complete wave fitting in the length of the vibrating section of the rod.
For a rod fixed at both ends, the fundamental frequency f1 is given by:
f1=vλ1
where λ1 is the wavelength of the fundamental mode. For the fundamental mode, the wavelength is twice the length of the vibrating section:
λ1=2L=2×40cm=80cm
Thus, the fundamental frequency is:
f1=v80
The harmonics for a rod fixed at both ends are given by:
fn=n⋅f1=n⋅v80
where n is the harmonic number (1, 2, 3, ...).
- The first overtone (second harmonic) corresponds to n=2:
f2=2⋅v80=v40
- The second overtone (third harmonic) corresponds to n=3:
f3=3⋅v80
- The third overtone (fourth harmonic) corresponds to n=4:
f4=4⋅v80=v20
- The second overtone is the fifth harmonic, which corresponds to n=5:
f5=5⋅v80=5v80=v16
- The third overtone is the sixth harmonic, which corresponds to n=6:
f6=6⋅v80=6v80=3v40
- The fundamental frequency is v80.
- The second overtone is the fifth harmonic.
- The frequency of the third overtone is 3v40.
The correct options based on the calculations are:
1. The fundamental frequency is v80.
2. The second overtone is the fifth harmonic.
3. The frequency of the third overtone is 3v40.
Similar Questions
A conducting rod of length l is moving in a transverse magnetic field of strength B with veocity v. The resistance of the rod is R. The current in the rod is
View SolutionA brass rod of length 1m is fixed to a vertical wall at one end, with the other end keeping free to expand. When the temperature of the rod is increased by 120∘C, the length increases by 3cm. What is the strain?
View Solution
Knowledge Check
- Question 1 - Select One
A uniform rod of length 1m mass 4kg is supports on tow knife-edges placed10cm from each end. A 60N weight is suspended at 30cm from one end. The reactions at the knife edges is.
Aa. 60 N, 40 NBb. 75 N, 25 NCc. 65 N, 35 NDd. 55 N, 45 N - Question 2 - Select One
A rod of length 10 cm lies along the principal axis of a concave mirror of focal length 10 cm in such a way that the end closer to the pole is 20 cm away from it. Find the length of the image.
A10cmB15cmC2.5cmD5cm
Object AB is placed on the axis of a concave mirror of focal length 10cm. End A of the object is at 30cm from the mirror. Find the length of the image
a. if length of object is 5cm.
b. if length of object is 1 mm.
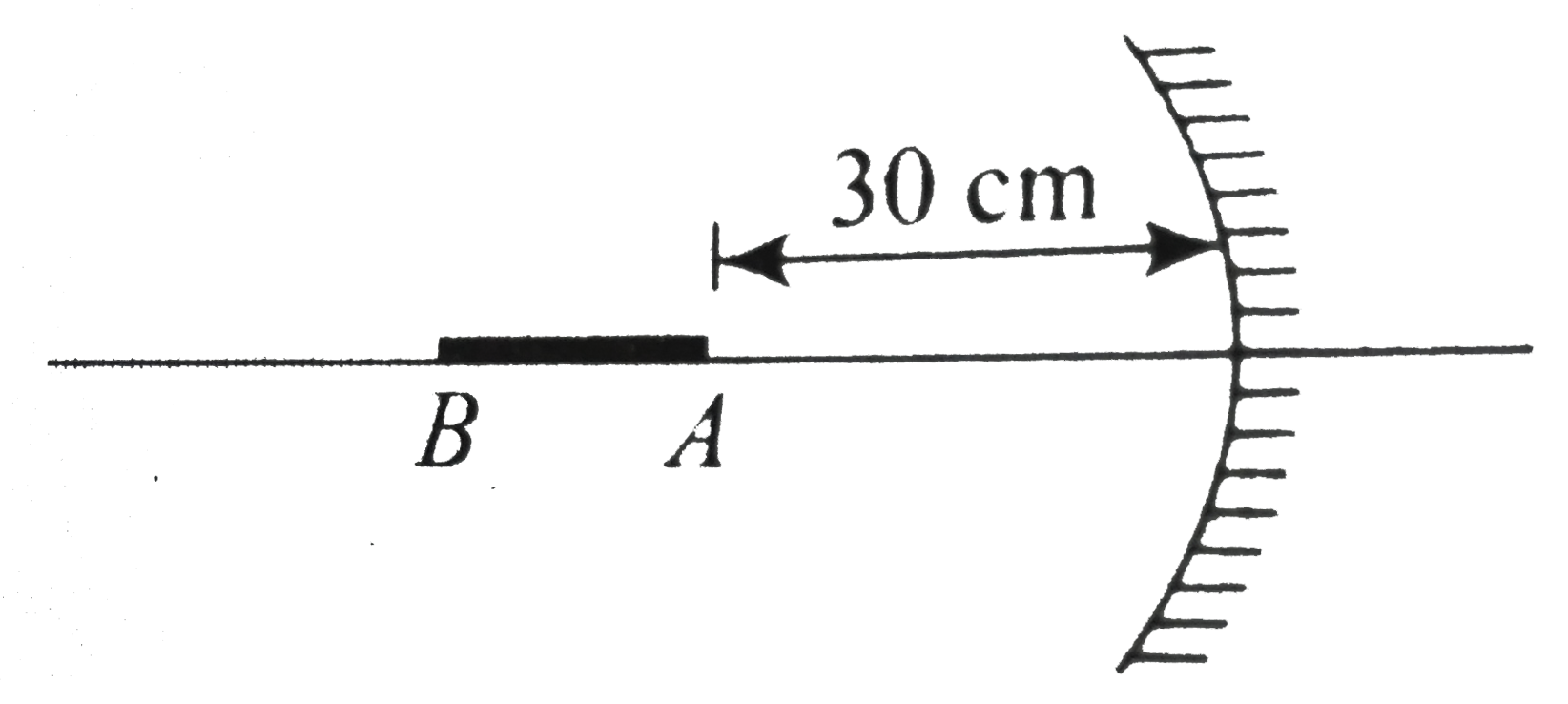 View Solution
View SolutionA particle of mass m=1kg collides with the end with velocity v0=6ms−1 of a spinning rod of mass2m and length l=1m at the end of the rod. If the coefficient of restitution of collision e=(2/3), find the
a. velocity of the particle
b. angular velocity of the rod just after the impact.
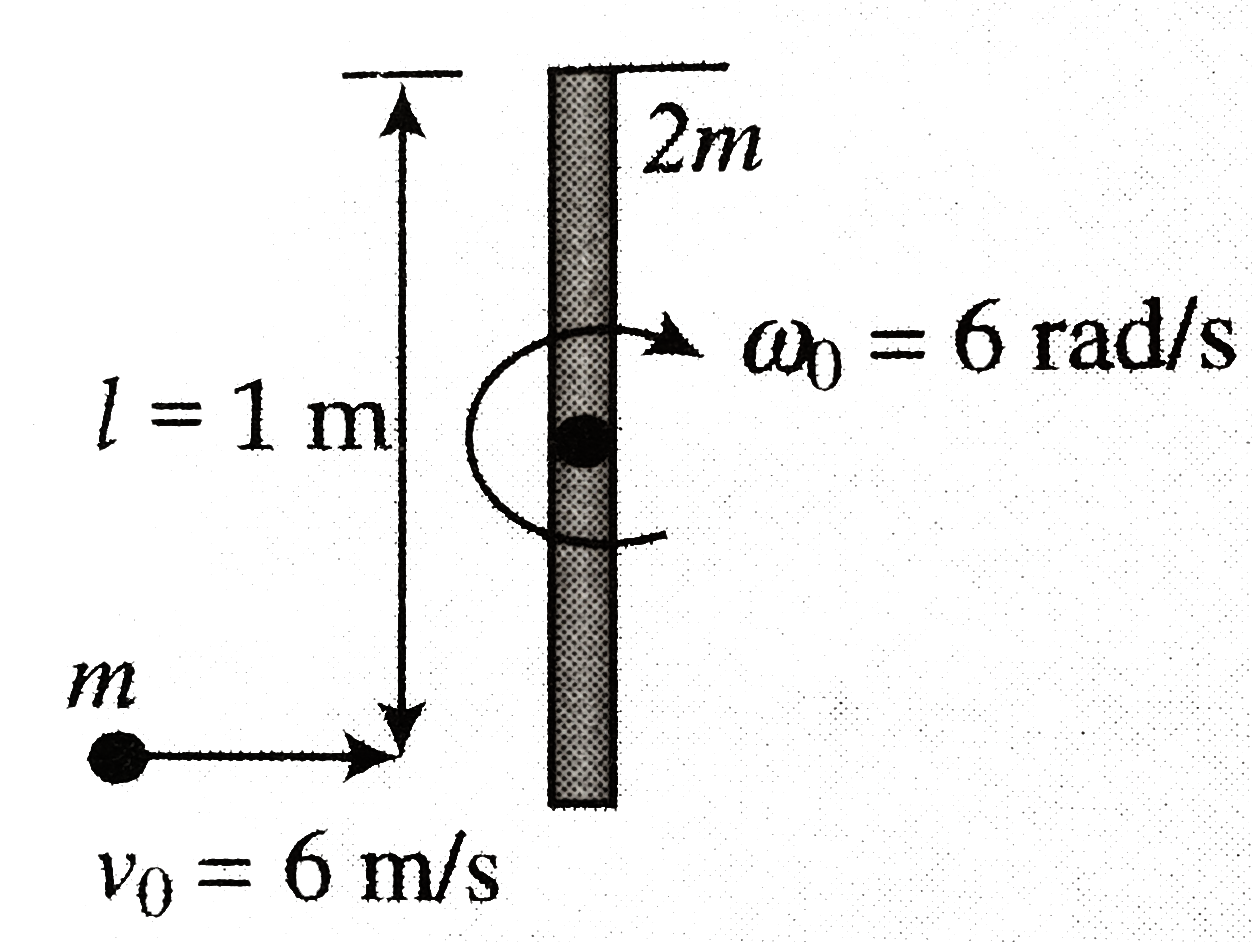 View Solution
View SolutionA rod of length L is sliding on a frictionless surface as shown in the figure. Velocity of end A is 4m/s along the wall. Find the velocity of end B, when end B makes 30∘ with wall PQ.
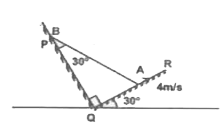 View Solution
View SolutionA metallic rod of length 1m is rigidly clamped at its mid point. Longirudinal stationary wave are setup in the rod in such a way that there are two nodes on either side of the midpoint. The amplitude of an antinode is 2×10−6m. Write the equation of motion of a point 2 cm from the midpoint and those of the constituent waves in the rod, (Young,s modulus of the material of the rod =2×1011Nm−2 , density =8000kg−m−3). Both ends are free.
View SolutionA rod of length 10 cm lies along the principal axis of a concave mirror of focal length 10 cm in such a way that the end closer to the pole is 20 cm away from it. Find the length of the image.
View SolutionA rod of length 10 cm lies along the principal axis of a concave mirror of focal length 10 cm in such a way that its end closer to the pole is 20cm away from the mirror. The length of the image is
View Solution

