A man of height =3/2m,wants to see himself in plane mirror from top to bottom. The plane mirror is inclined with vertical wall at angle α=53∘. If the least size of mirror to see him 3nm, the distance of eye from mirror is d=3m, find the value of m
The correct Answer is:8
To solve the problem, we need to find the value of n given the height of the man, the angle of inclination of the mirror, and the distance of the eye from the mirror.
1. Identify the given values:
- Height of the man, h=32m
- Angle of inclination of the mirror, α=53∘
- Distance of the eye from the mirror, d=3m
- The least size of the mirror to see himself is given as 3nm.
2. Understand the geometry of the situation:
- The man wants to see his full height in the mirror. The mirror is inclined at an angle α with the vertical wall.
- The height of the mirror must be sufficient to reflect the entire height of the man.
3. Use the tangent function:
- From the triangle formed by the man, the eye, and the mirror, we can use the tangent function to relate the height of the man to the distance from the eye to the mirror:
tan(θ)=hd
where θ is the angle of elevation from the eye to the top of the man.
4. Apply the sine rule:
- In triangle EAB (where E is the eye, A is the top of the man, and B is the bottom of the man), we can apply the sine rule:
hsin(2θ)=Tcos(θ)
where T is the length of the mirror.
5. Manipulate the equations:
- Rearranging gives us:
h⋅cos(θ)=T⋅sin(2θ)
- Using the identity sin(2θ)=2sin(θ)cos(θ):
h⋅cos(θ)=T⋅2sin(θ)cos(θ)
- This simplifies to:
T=h⋅cos(θ)2sin(θ)
6. Substituting known values:
- We know h=32 m and d=3 m. We can find θ using:
tan(θ)=hd=323=12
- Therefore, θ=tan−1(12).
7. Calculate the size of the mirror:
- Substitute θ back into the equation for T:
T=32⋅cos(θ)2sin(θ)
- We can find cos(θ) and sin(θ) using trigonometric identities.
8. Relate the size of the mirror to n:
- The least size of the mirror is given as T=3n.
- Set the two expressions for T equal to each other and solve for n:
32⋅cos(θ)2sin(θ)=3n
- This leads to:
n=3⋅2sin(θ)3⋅cos(θ)=2sin(θ)cos(θ)=2tan(θ)
9. Final calculation:
- Substitute tan(θ)=12:
n=2⋅12=1
Final Answer:
The value of n is 8.
- Height of the man, h=32m
- Angle of inclination of the mirror, α=53∘
- Distance of the eye from the mirror, d=3m
- The least size of the mirror to see himself is given as 3nm.
- The man wants to see his full height in the mirror. The mirror is inclined at an angle α with the vertical wall.
- The height of the mirror must be sufficient to reflect the entire height of the man.
- From the triangle formed by the man, the eye, and the mirror, we can use the tangent function to relate the height of the man to the distance from the eye to the mirror:
tan(θ)=hd
where θ is the angle of elevation from the eye to the top of the man.
- In triangle EAB (where E is the eye, A is the top of the man, and B is the bottom of the man), we can apply the sine rule:
hsin(2θ)=Tcos(θ)
where T is the length of the mirror.
- Rearranging gives us:
h⋅cos(θ)=T⋅sin(2θ)
- Using the identity sin(2θ)=2sin(θ)cos(θ):
h⋅cos(θ)=T⋅2sin(θ)cos(θ)
- This simplifies to:
T=h⋅cos(θ)2sin(θ)
- We know h=32 m and d=3 m. We can find θ using:
tan(θ)=hd=323=12
- Therefore, θ=tan−1(12).
- Substitute θ back into the equation for T:
T=32⋅cos(θ)2sin(θ)
- We can find cos(θ) and sin(θ) using trigonometric identities.
- The least size of the mirror is given as T=3n.
- Set the two expressions for T equal to each other and solve for n:
32⋅cos(θ)2sin(θ)=3n
- This leads to:
n=3⋅2sin(θ)3⋅cos(θ)=2sin(θ)cos(θ)=2tan(θ)
- Substitute tan(θ)=12:
n=2⋅12=1
The value of n is 8.
Similar Questions
Knowledge Check
A man standing in front of a plane mirror finds his image to be at a distance of 6 metre from himself. The distance of man from the mirror is :
A6mB3mC2mD12m
A man standing in front of a plane mirror finds his image at a distance 6 metre from himself. What is the distance of man from the mirror?
View SolutionA man standing in front of a plane mirror finds his image at a distance 6 metre from himself. What is the distance of man from the mirror?
View SolutionTwo plane mirrors are inclined at 70∘. A ray incident on one mirror at incidence angle θ after reflection falls on the second mirror and is reflected from there parallel to the first mirror, The value of θ is
View SolutionAn object placed in front of a plane mirror is displaced by 0.4 m along a straight line at an angle of 30∘ to mirror plane. The change in the distance between the object and its image is:
View SolutionA man is standing at distance x from a plane mirror in front of him. He wants to see the entire wall in mirror which is at distance. y behind the man. Find the minimum size of the mirror required.
View SolutionA point source of light ,S is placed at a distance L in front of the centre of plane mirror of width d which is a hanging vertically on wall ,A man walks in front of the mirror , at a distance 2L as shown below . The distance over which the man can see the image of the light source in the mirror is :
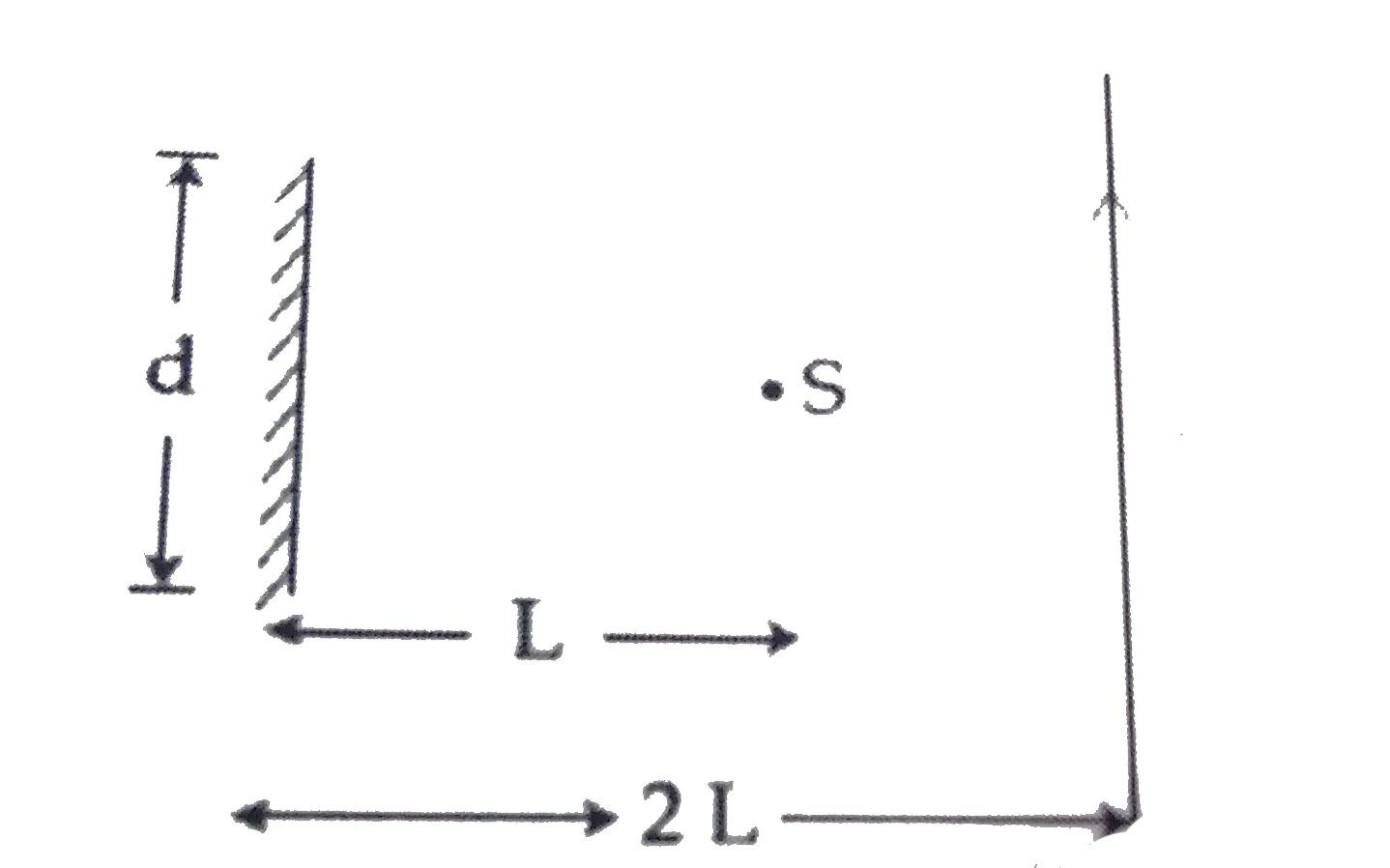
View SolutionThe figure shows two plane mirrors parallel to each other and an object O placed between them. Then , the distances of the first three images from the mirror M2 will be (in cm)
View Solution
