A heavy disc with radius R is rolling down hanging on two non-stretched string wound around the disc very tightly. The free ends of the string are attached to a fixed horizontal support. The strings are always tensed during the motion. At some instant, the angular velocity of the disc is ω, and the angle between the strings is α. Find the velocity of centre of mass of the disc at this moment

The velocities of point A and B being perpendicular to the strings, the instantaneous axis of rotation must be at D, instantaneous point of intersection of the line of the two strings.
Therefore,
VCM=ω.OD=ω×OBcos.α2=ωRcos.α2

Similar Questions
A disc of the radius R is confined to roll without slipping at A and B. If the plates have the velocities v and 2v as shown, the angular velocity of the disc is
 View Solution
View Solution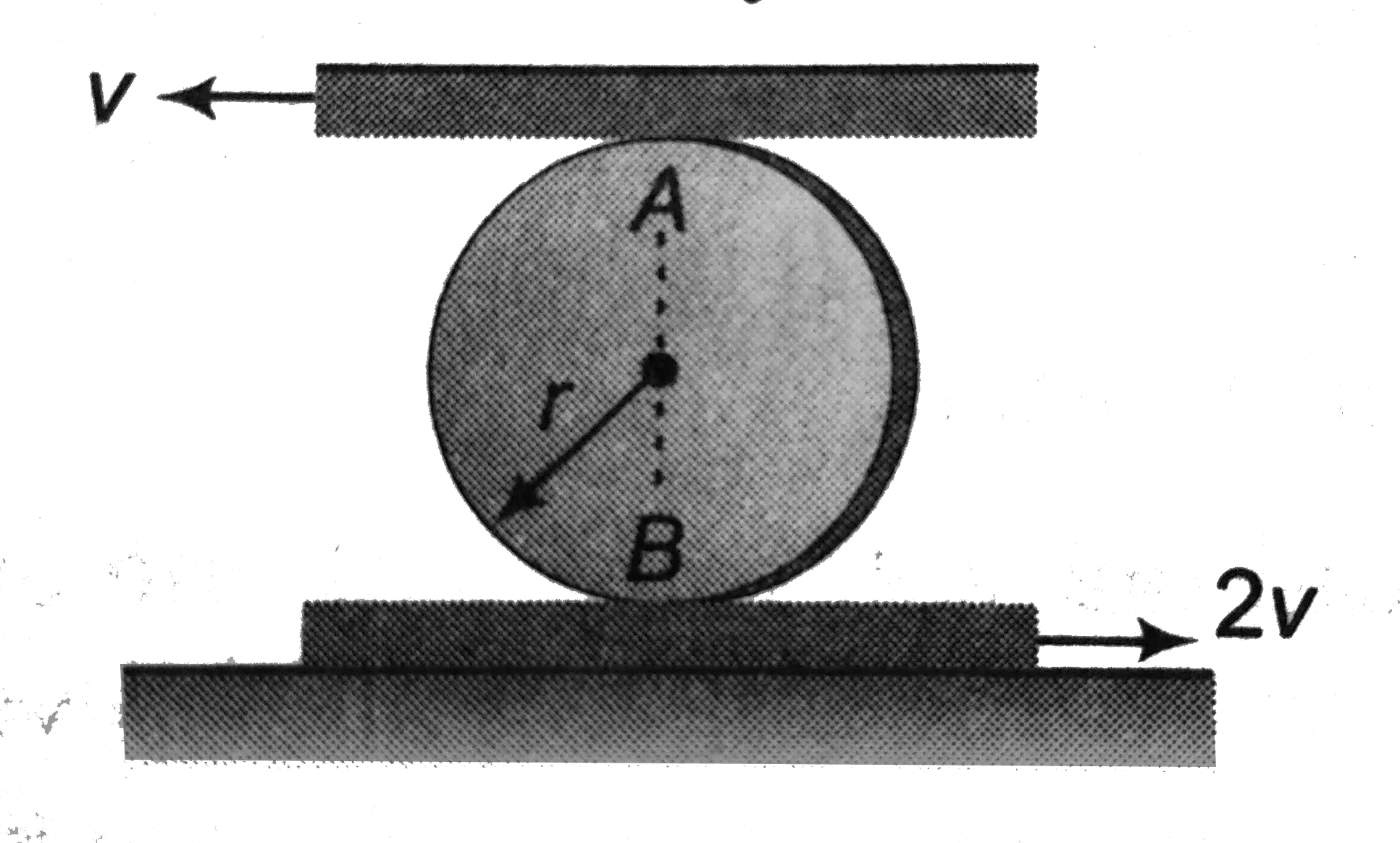
the disc of the radius r is confined to roll without slipping at A and B if the plates have the velocities shown, determine the angular velocity of the disc.View SolutionFind the position of instantaneous centre of rotation and angular velocity of the disc in the following cases as shown. Radius of disc is R in each case.
 View Solution
View Solution
A thread is wound around two discs on either sides. The pulley and the two discs have the same mass and radius. There is no slipping at the pulley and no friction at the hinge. Find out the acceleration of the two discs and the angular acceleration of the pulley.View Solution
A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity the angle between the velocity ad acceleration vectors of point P isView Solution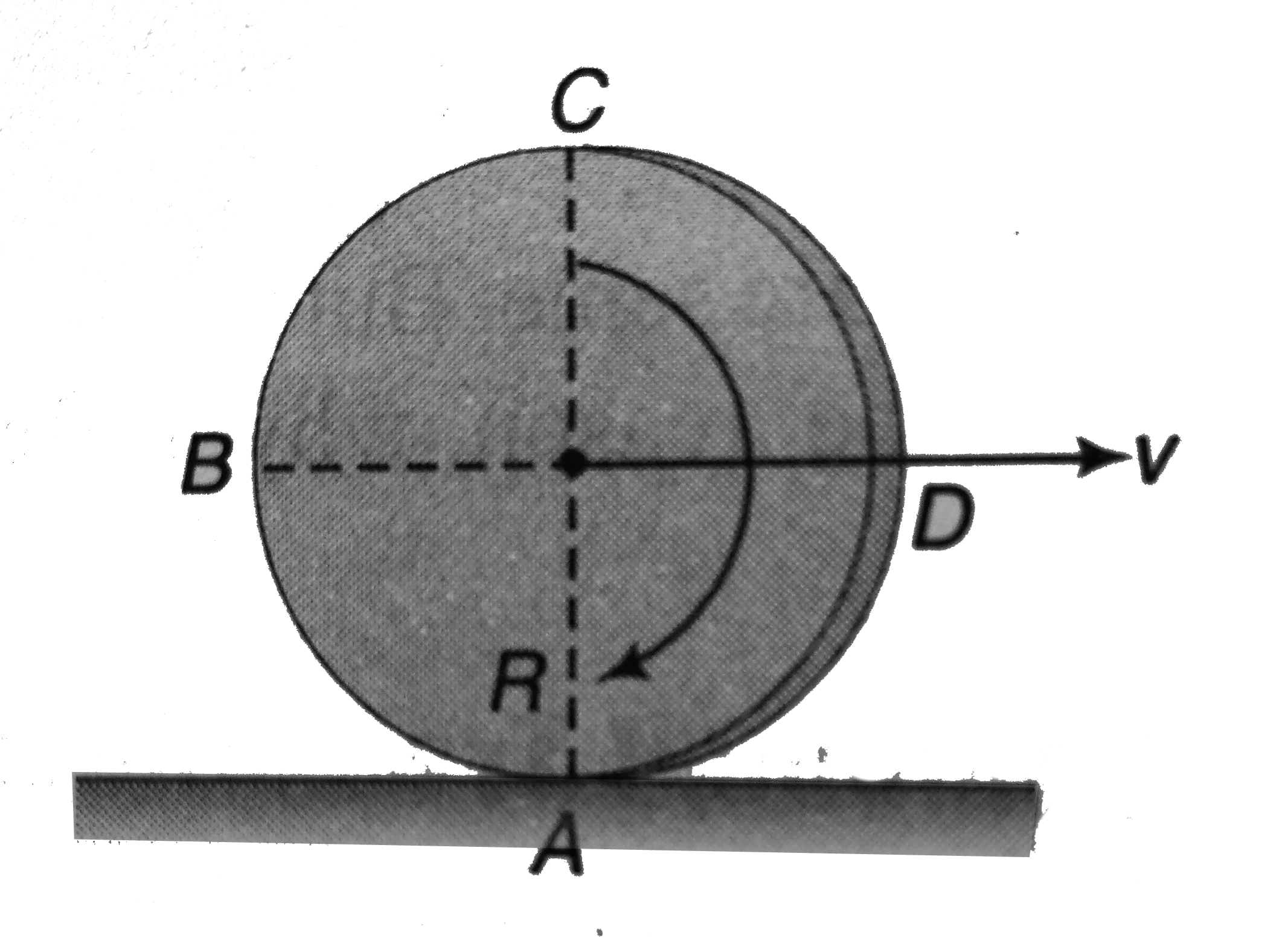
A disc of radius R has linear velocity v and angular velocity ω as shown in the figure. Given υ=rω find velocity of point A, B, C and D on the disc.View SolutionA disc of radius R has a light pole fixed perpendicular to the disc at its periphery which in turn has a pendulum of length R attached to its other end as shown in figure. The disc is rotated with a constant angular velocity ω The string is making an angle 45∘ with the rod. Then the angular velocity ω of disc is
 View Solution
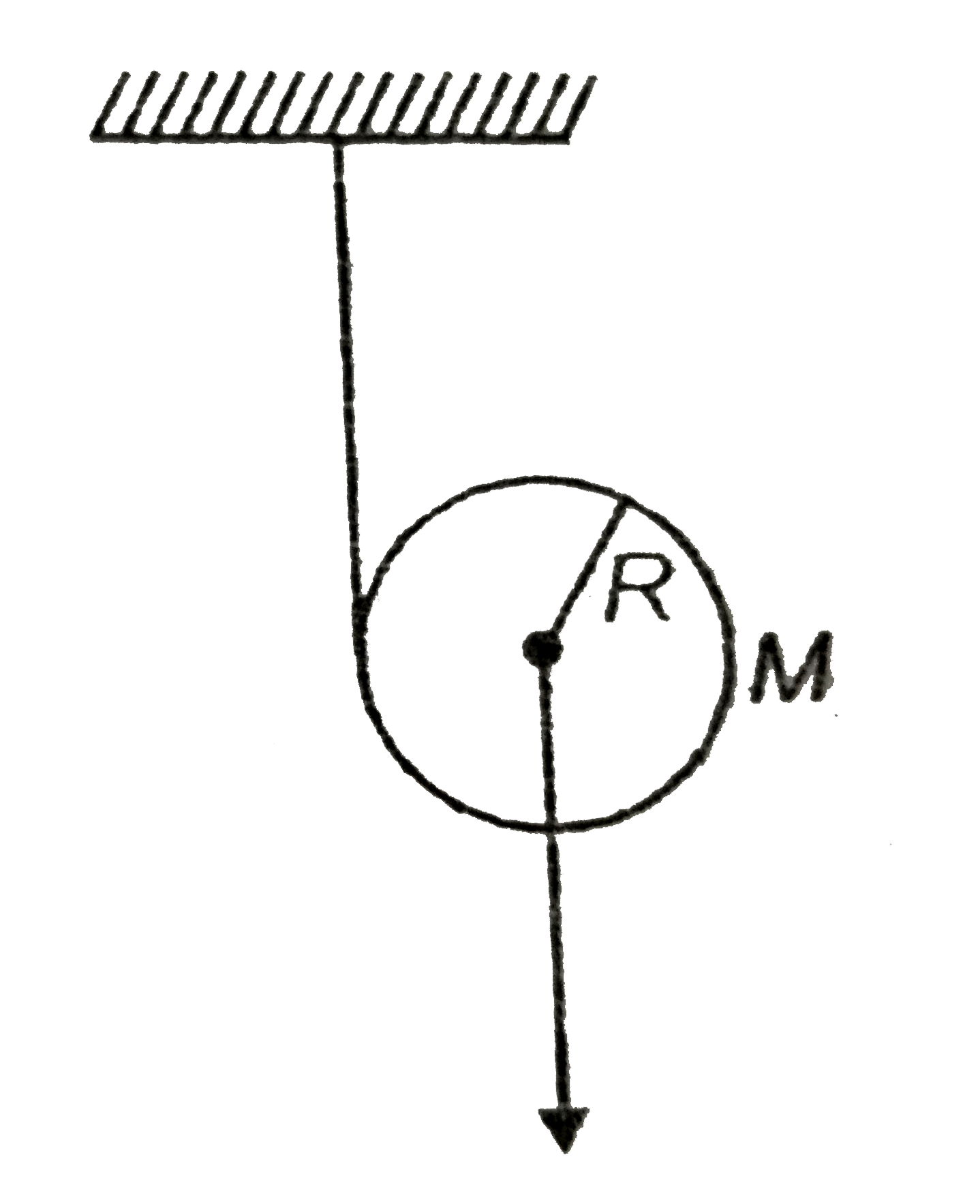
View SolutionA disc of mass M has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the ceiling and the disc is released from rest. Find the acceleration of the disc and the tension in the string.
 View Solution
View SolutionA uniform disc of mass M, radius R is attached to a frictionless horizontal axis. Its rim is wound with a light string and a tension T is applied to it, the angular acceleration will be?
View SolutionInitial angular velocity of a circular disc of mass M is ω1. Then two small spheres of mass m are attached gently to two diametrically opposite points on the edge of the disc. What is the final angular velocity of the disc -
View Solution

