A uniform disc of mass M, radius R is attached to a frictionless horizontal axis. Its rim is wound with a light string and a tension T is applied to it, the angular acceleration will be?
2T/M
2T/MR
T/MR
T/M
The correct Answer is:B
To find the angular acceleration of a uniform disc of mass M and radius R when a tension T is applied to a string wound around its rim, we can follow these steps:
Step 1: Understand the system
We have a uniform disc with mass M and radius R. The disc is mounted on a frictionless horizontal axis, and a string is wound around its rim. When tension T is applied to the string, it creates a torque that causes the disc to rotate.
Step 2: Calculate the torque due to the tension
The torque (τ) caused by the tension T can be calculated using the formula:
τ=T⋅R
where R is the radius of the disc.
Step 3: Relate torque to angular acceleration
Torque can also be expressed in terms of the moment of inertia (I) and angular acceleration (α) using the formula:
τ=I⋅α
For a uniform disc, the moment of inertia (I) is given by:
I=12MR2
Step 4: Set the two expressions for torque equal to each other
From Step 2 and Step 3, we can set the two expressions for torque equal:
T⋅R=12MR2⋅α
Step 5: Solve for angular acceleration (α)
We can rearrange the equation to solve for angular acceleration (α):
α=2TMR
Final Answer
Thus, the angular acceleration of the disc is given by:
α=2TMR
We have a uniform disc with mass M and radius R. The disc is mounted on a frictionless horizontal axis, and a string is wound around its rim. When tension T is applied to the string, it creates a torque that causes the disc to rotate.
The torque (τ) caused by the tension T can be calculated using the formula:
τ=T⋅R
where R is the radius of the disc.
Torque can also be expressed in terms of the moment of inertia (I) and angular acceleration (α) using the formula:
τ=I⋅α
For a uniform disc, the moment of inertia (I) is given by:
I=12MR2
From Step 2 and Step 3, we can set the two expressions for torque equal:
T⋅R=12MR2⋅α
We can rearrange the equation to solve for angular acceleration (α):
α=2TMR
Thus, the angular acceleration of the disc is given by:
α=2TMR
Topper's Solved these Questions
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE D
10 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
Similar Questions
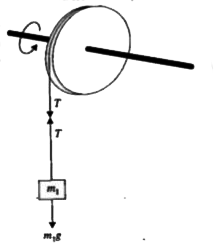
A wheel of mass 1.4 kg and radius 0.4 m is mounted on a frictionless, horizontal axle as shown in Fig. 7.2.50. Alight string wrapped around the rim supports a mass of 2 kg. What is the angular acceleration of the wheel and the tangential acceleration of a point on the rim ? Also find the tension in the string.
View SolutionA uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
View Solution
A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω . Another disc of same dimensions but of mass 14 M is placed gently on the first disc co-axially. The angular velocity of the system is
View SolutionA uniform disc of mass M and radius R is mounted on an axle supported in frictionless bearings. A light cord is wrapped around the rim of the disc and a steady downward pull T is exerted on the cord. The angular acceleration of the disc is
View SolutionA uniform disc of mass M and radius R is liffted using a string as shown in the figure. Then choose incorrect option(s),

View SolutionA uniform disc of radius R and mass M is free to rotate about a fixed horizontal axis perpendicular to its plane and passing through its centre. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The block is released from rest. If string does not slip on the rim then find the acceleration of the block. Neglect the mass of the string.
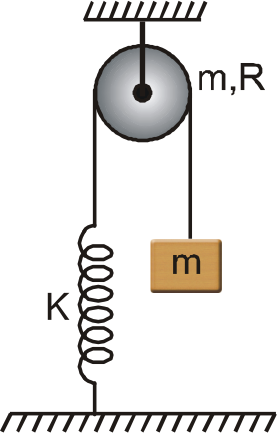
View SolutionA uniform disc of mass m and radius R is free to rotate about its fixed horizontal axis without friction. There is sufficient friction between the inextensible light string and disc to prevent slipping of string over disc. At the shown instant extension in light spring is 3mgK, where m is mass of block, g is acceleration due to gravity and K is spring constant. Then select the correct alternative(s).
View SolutionA uniform disc of mass of 0.50 kg and radius 0.20 m lies on one side initially at rest on a frictionless horizontal surface. A constant force of 3 N is then applied tangentially at its perimeter using a light weight cord wrapped aroutid its edge. What is the (i) angular acceleration (ii) angular velocity and angular displacement after 2s ?
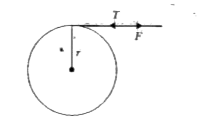
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View Solution
